Вычислительная математика
Метод половинного деления для уравнения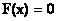 
для непрерывной функции 
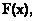удовлетворяющей на отрезке [ a , b ] условию 
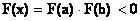сходится
для непрерывной функции удовлетворяющей на отрезке [ a , b ] условию сходитсяпри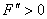 
при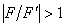 
всегда
при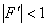 
Условия Фурье заключаются в выполнении условий
F(x), F′(x) непрерывны, F″(x0) > 0
F″(x), F″′(x) знакопостоянны, F(x0) ≠ 0
F′(x) > 0, F″(x) ≠ 0, F′(x0) > 0
F′(x), F″(x) знакопостоянны, F(x0)F″(x0) > 0
Уравнение записано в виде, удобном для итераций: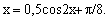 
Первое приближение метода итераций x1 для начального приближения 
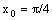равно
Первое приближение метода итераций x1 для начального приближения равно3π ∕ 8
3π ∕ 4
π ∕ 4
π ∕ 8
Задана линейная система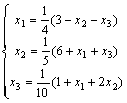 
. Начиная с начального значения 
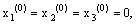один шаг метода Зейделя 
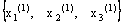будет равен
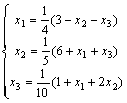. Начиная с начального значения один шаг метода Зейделя будет равен{ 0,75 ; 1,2 ; 0,445 }
{ 0,75 ; 1,35 ; 0,05 }
{ 0,75 ; 1,2 ; 0,1 }
{ 0,75 ; 1,35 ; 0,445 }
Из приведенных уравнений: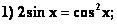
; 
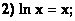
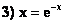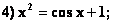
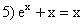- вид, удобный для итераций, имеют уравнения
; - вид, удобный для итераций, имеют уравнения2, 3 и 5
1 и 2
3, 4 и 5
2, 4 и 5
Разностная схема называется устойчивой, если
она аппроксимирует дифференциальное уравнение
она определяет решение, не выходящее за круг данного радиуса
решение разностной схемы стремится к константе
малому изменению входных данных соответствует малое изменение решения
В таблично заданной функции производная в точке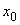 
вычислена с использованием шагов h и 2h. Получены величины 
= 1,5 и 
= 1,3. Погрешность формулы для вычисления производных имеет порядок 
. Тогда уточненное значение производной 
по методу Рунге равна
вычислена с использованием шагов h и 2h. Получены величины 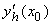= 1,5 и 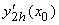= 1,3. Погрешность формулы для вычисления производных имеет порядок 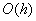. Тогда уточненное значение производной 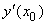по методу Рунге равна1,7
1,65
1,6
1,4
Собственные значения матрицы А расположены в порядке убывания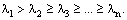 
Степенной метод нахождения λ1 сходится, если
Степенной метод нахождения λ1 сходится, если
Для таблично заданной функции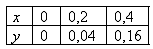
вычисление y(0,1) с помощью линейной интерполяции дает результат
вычисление y(0,1) с помощью линейной интерполяции дает результат0,02
0,22
0,01
0,03
Вырожденным называется ядро интегрального уравнения вида
K( x, s ) = f ( x ).
K( x, s ) = K( s, x )
K( x, s ) = 0 при x = s
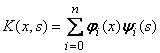
Квадратурная формула Симпсона является точной для подынтегральной функции, имеющей вид многочлена степени
3
2
4
5
Точечной называется аппроксимация называется, если
значения аппроксимирующей и аппроксимируемой функции совпадают в граничных точках отрезка
для построения аппроксимирующей функции φ(x) используются точки, выбранные случайным образом
аппроксимирующая функция φ(x) строится на дискретном множестве точек
аппроксимирующая функция φ(x) вычисляется по значениям функции и ее производных в одной точке
Для линейной системы уравнений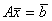 
известно LU-разложение матрицы 
Тогда количество систем уравнений с треугольными матрицами, к которым сводится решение исходной системы уравнений равно
известно LU-разложение матрицы 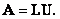Тогда количество систем уравнений с треугольными матрицами, к которым сводится решение исходной системы уравнений равнотрем
двум
единице
четырем
Один шаг метода простой итерации для нелинейного уравнения вида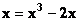 
и начального приближения 
, дает
и начального приближения 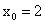, даетx1 = 1
x1 = 10
x1 = 4
x1 = 2,5
При вычислении интеграла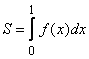 
подынтегральная функция задана таблицей Метод трапеций с h = 0,5 дает значение интеграла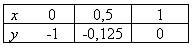
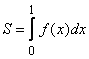подынтегральная функция задана таблицей Метод трапеций с h = 0,5 дает значение интеграла-0,25
-0,3
-0,3125
-0,275
имеет собственные значения:Дана матрица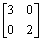 
и вектор 
. Результатом первого шага степенного метода является вектор
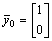и вектор . Результатом первого шага степенного метода является вектор
Метод Зейделя для системы линейных уравнений с матрицей A обладает следующими достаточными условиями сходимости
( 1 ≤ j ≤ n , j ≠ i , i = 1, 2, . . . n )
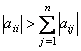( i = 1, 2, . . . n ; j = 1, 2, . . . n )aii ≠ 0 ( i = 1, 2, . . . n )
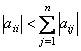( i = 1, 2, . . . n ; j = 1, 2, . . . n )Для задачи Коши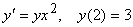 
один шаг метода Эйлера с h = 0,1 дает результат для y(2,1), равный
один шаг метода Эйлера с h = 0,1 дает результат для y(2,1), равный4,2
3,5
4,1
3,2
Дана система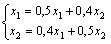 
. Первое приближение для метода простой итерации с начальным приближением 
будет равно
. Первое приближение для метода простой итерации с начальным приближением 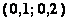будет равно( 0,13 ; 0,14 )
( 0,9 ; 0,9 )
( 0,14 ; 0,13 )
( 0,5 ; 0,4 )
Если для величин x = 2 и y = 8 относительные погрешности равны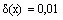
и 
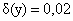, то относительная погрешность суммы 
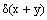равна
и , то относительная погрешность суммы равна0,016
0,018
0,03
0,003
Результат одного шага метода Ньютона для уравнения x3 - x = 0 и начального приближения x0 = 1. равен
x1 = 0,5
x1 = 2
x1 = 1
x1 = −1
Глобальной называется интерполяция, у которой
интерполяционный многочлен является общим на бесконечном интервале ( − ∞‚ ∞ )
она вычисляется по общим формулам для всех видов функции φ(x)
один интерполяционный многочлен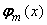 
используется для интерполяции исходной функции f(x) на всем интервале [a, b]
используется для интерполяции исходной функции f(x) на всем интервале [a, b]один интерполяционный многочлен позволяет описать любую непрерывно дифференцируемую функцию
Заданы нелинейные уравнения вида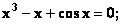 
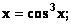
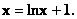Вид, удобный для итераций, имеют следующие уравнения
Вид, удобный для итераций, имеют следующие уравнениявторое
первое и второе
первое
второе и третье
Наименее уклоняющимся от нуля многочленом будет многочлен
Чебышева
Ньютона
Лагранжа
Гаусса
Для таблично заданной функции y = f(x) первая производная на правом конце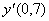 
с погрешностью 
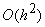равна
с погрешностью равна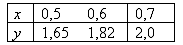1,8
2
1,92
1,85
Условие устойчивости явной разностной схемы для одномерного нестационарного уравнения теплопроводности имеет вид
Метод Симпсона на элементарном отрезке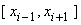 
имеет погрешность порядка k, равного
имеет погрешность порядка k, равного3
4
2
5
Сходимость итерационного метода решения систем линейных уравнений зависит от
количества нулей в матрице
величины правых частей системы
вида матрицы системы
начального приближения системы
Порядком разностного уравнения называется
количество конечных разностей, входящих в уравнение
наибольший аргумент функции
количество последовательных точек, задание решения в которых позволяет выделить единственное решение
наибольшая степень неизвестной функции
имеет вид
U = 
U = 
U = 
Если абсолютные погрешности величин x и y равны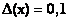 
и 
, то абсолютная погрешность суммы 
будет равна
и 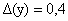, то абсолютная погрешность суммы 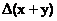будет равна−0,3
0,5
0,2
0,3
Примем, что функция F( x ) на отрезке [ a , b ] непрерывна, причем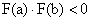 
. Тогда метод половинного деления для уравнения сходится
. Тогда метод половинного деления для уравнения 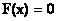сходитсявсегда
если F( x ) ∙ F′( x ) > 0
при F′( x ) > 0
при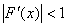 
Метод Гаусса заключается в сведении исходной матрицы системы к эквивалентному виду, где матрица преобразованной системы является
верхней треугольной матрицей
диагональной матрицей
симметричной матрицей
ленточной матрицей
Для дифференциального уравнения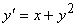 
при начальном условии y(0)=1 один шаг метода Эйлера при h = 0,2 дает значение
при начальном условии y(0)=1 один шаг метода Эйлера при h = 0,2 дает значение1,1
1,25
1,5
1,2
При вычислении интеграла 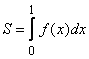подынтегральная функция задана таблицей Метод Симпсона с h = 0,5 дает значение интеграла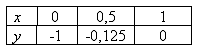
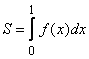подынтегральная функция задана таблицей Метод Симпсона с h = 0,5 дает значение интеграла-0,3125
-0,375
-0,25
-0,3
Для решения задачи Коши обыкновенного дифференциального уравнения формулы метода Эйлера с пересчетом имеют вид
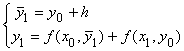
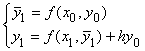
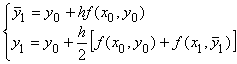
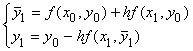
Один шаг метода Эйлера для задачи Коши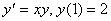 
с шагом h = 0,1 дает результат
с шагом h = 0,1 дает результат2,2
0
2
2,4
Один шаг метода Ньютона для нелинейного уравнения вида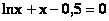 
и начального приближения 
, дает
и начального приближения 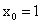, даетx1 = 1,5
x1 = 0,75
x1 = 1,25
x1 = 0,5
Дана система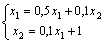 
задано начальное приближение 
Один шаг метода Зейделя дает первое приближение
задано начальное приближение 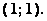Один шаг метода Зейделя дает первое приближение( 0,6 ; 1,06 )
( 0,6 ; 1 )
( 0,1 ; 1,06 )
( 0,6 ; 1,1 )
Интерполяцией называется такая аппроксимация исходной функции f(x) интерполирующей функцией φ(x), при которой
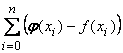минимальна
Квадратурная формула Гаусса для n точек разбиения является точной для многочлена степени
2n
2n - 1
2n + 1
n
Дана система линейных уравнений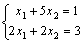 
. Для сходящегося метода Зейделя ее надо записать в виде
. Для сходящегося метода Зейделя ее надо записать в виде
При вычислении определенного интеграла методом Симпсона используют аппроксимацию подынтегральной функции
кусочно-постоянной функцией
кусочно-линейной функцией
квадратичной функцией
кубическим сплайном
Погрешность математической модели является
возрастающей
регулируемой
неустранимой
вычислительной
При вычислении интеграла 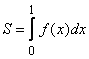подынтегральная функция задана таблицей. Метод трапеций с h = 0,5 дает значение интеграла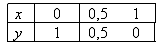
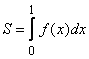подынтегральная функция задана таблицей. Метод трапеций с h = 0,5 дает значение интеграла1,5
1
2∕3
0,5
Интеграл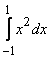 
, вычисленный методом трапеций с разбиением на два интервала (h = 1), равен
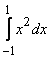, вычисленный методом трапеций с разбиением на два интервала (h = 1), равен1
0,5
0,333333
0,25