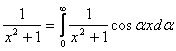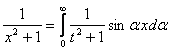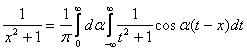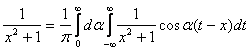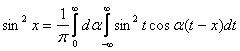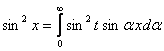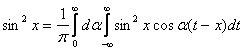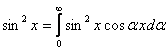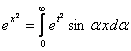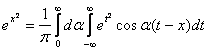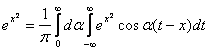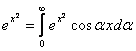Уравнения математической физики (курс 2)
______________________ - метод решения дифференциальных уравнений, который позволяет от одного уравнения перейти к нескольким уравнениям, но с меньшим числом независимых переменных
Метод разделения переменных
Метод дифференциальных преобразований
Метод преобразования Фурье
Метод интегральных преобразований
Cинус-преобразование Фурье функции f(x) записывается в виде: Fs(a) = 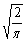
 f(x)sinax dx. Найти синус-преобразование Фурье функции
f(x)sinax dx. Найти синус-преобразование Фурье функции 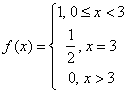
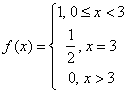
Интегралом Фурье по косинусам функции f(x) называется выражение вида
f(x)=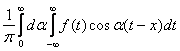
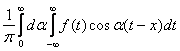
cos x=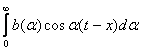
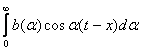
f(x)=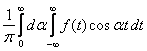
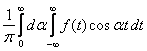
f(x)=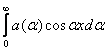
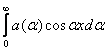
Верны ли утверждения? А) Преобразование Фурье – нелинейное преобразование Б) Для функций 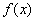 и
и 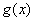 ,
, 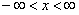 , справедлива формула
, справедлива формула 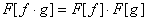 .
.
А - нет, Б - да
А - да, Б - нет
А – да, Б - да
А - нет, Б - нет
Преобразование Фурье F[f] функций удовлетворяет свойству линейности
F[K1f + K2g] = K1F[f] + K2F[g]
F[K1f × K2g] = K1F[f] × K2F[g]
F[K1f + K2g] = K1F[f] × K2F[g]
F[K1f × K2g] = K1F[f] + K2F[g]
Коэффициент А(l) в задаче Коши для уравнения теплопроводности Ut = Uxx, U(x,0) = j(x) вычисляется по формуле А(l) = 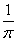
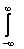 j(x)cosx
j(x)cosx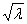 dxТогда коэффициент А(l) при U(x,0) = j(x) = sinx равен
dxТогда коэффициент А(l) при U(x,0) = j(x) = sinx равен
0
-1
1
3
Интегралом Фурье функции f(x)=x2 называется выражение вида
x2 =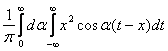
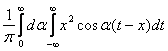
x2 =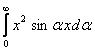
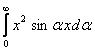
x2 =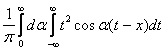
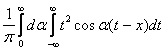
x2 =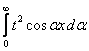
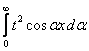
Решение задачи Коши для уравнения теплопроводности Ut = Uxx с начальным условием U(x,0) = j(x)= имеет вид
имеет вид
U(x,t) = 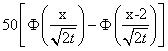
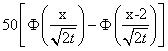
U(x,t) =50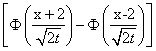
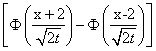
U(x,t) = 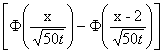
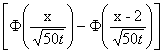
U(x,t) = 

Функция 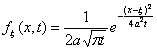 , которая при всех
, которая при всех 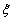 является решением уравнения теплопроводности при всех -
является решением уравнения теплопроводности при всех - <>
<> и t>0- это
и t>0- это
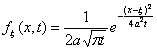 , которая при всех
, которая при всех обратное преобразование Фурье
свертка функций
формула Пуассона решения задачи Коши для уравнения теплопроводности
фундаментальное решение уравнения теплопроводности
Верны ли утверждения? А) Функция Хэвисайда - 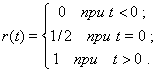 Б) Задача Коши для однородного уравнения теплопроводности - уравнение
Б) Задача Коши для однородного уравнения теплопроводности - уравнение 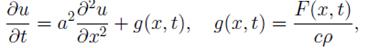 удовлетворяющего начальному условию
удовлетворяющего начальному условию 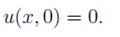
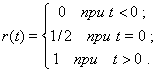 Б) Задача Коши для однородного уравнения теплопроводности - уравнение
Б) Задача Коши для однородного уравнения теплопроводности - уравнение А – да, Б - да
А - да, Б - нет
А - нет, Б - да
А - нет, Б - нет
Верны ли утверждения? А) Если функция 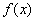 определена при
определена при 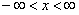 , то ее обратным преобразованием Фурье F
, то ее обратным преобразованием Фурье F 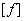 называется функция
называется функция 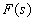 , которая определяется по формуле
, которая определяется по формуле 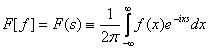 Б) В случае, когда функция
Б) В случае, когда функция 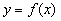 задана только на полупрямой
задана только на полупрямой 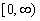 , ее можно представить в виде интеграла Фурье по косинусам или по синусам, если продолжить в интервал, соответственно, четным или нечетным образом
, ее можно представить в виде интеграла Фурье по косинусам или по синусам, если продолжить в интервал, соответственно, четным или нечетным образом
А – да, Б - да
А - нет, Б - да
А - нет, Б - нет
А - да, Б - нет
Верны ли утверждения? А) Функция Хэвисайда – r(t)=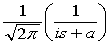 Б) Свойство свертки - для функций
Б) Свойство свертки - для функций  и
и  ,
,  , справедлива формула
, справедлива формула 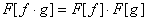
А - да, Б - нет
А – да, Б - да
А - нет, Б - да
А - нет, Б - нет
Верны ли утверждения? А) Метод разделения переменных – позволяет от одного уравнения перейти к нескольким уравнениям, но с меньшим числом независимых переменных (в частности, к обыкновенным дифференциальным уравнениям) Б) Интегральное преобразование определяется формулой 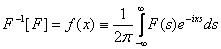
А – да, Б - да
А - да, Б - нет
А - нет, Б - нет
А - нет, Б - да
Выражение вида F(s) =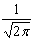
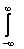 f(x)e-ixsdx называется
f(x)e-ixsdx называется
коэффициентом Фурье
преобразованием Фурье функции f(x)
интегралом Фурье
разложением Фурье
Верны ли утверждения? А) Абсолютно сходящийся несобственный интеграл - несобственный интеграл 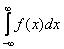 в том случае, если сходится интеграл
в том случае, если сходится интеграл  . Б) Кривая Гаусса - график фундаментального решения уравнения теплопроводности при фиксированных значениях
. Б) Кривая Гаусса - график фундаментального решения уравнения теплопроводности при фиксированных значениях 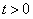 и
и 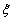
А - нет, Б - да
А - нет, Б - нет
А – да, Б - да
А - да, Б - нет
Преобразованием Фурье функции f(x) называется функция вида
F(s) = 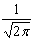
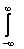 f(x)e-xsdx
f(x)e-xsdx
F(s) 

F(s) = 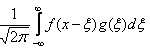
F(s) = 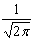
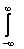 f(x)e-ixsdx
f(x)e-ixsdx
Верны ли утверждения? А) Интеграл Фурье функции 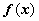 по синусам - представление функции в виде
по синусам - представление функции в виде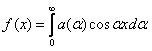 , где
, где 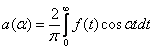 Б) Интеграл Фурье функции - представление функции в виде
Б) Интеграл Фурье функции - представление функции в виде 
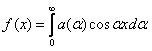 , где
, где 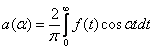 Б) Интеграл Фурье функции - представление функции в виде
Б) Интеграл Фурье функции - представление функции в виде 
А - нет, Б - да
А - да, Б - нет
А - нет, Б - нет
А – да, Б - да
Cинус-преобразование Фурье функции f(x) записывается в виде: Fs(a) = 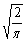
 f(x)sinax dx. Найти синус-преобразование Фурье функции
f(x)sinax dx. Найти синус-преобразование Фурье функции 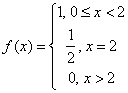
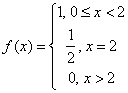
Несобственный интеграл 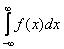 в том случае, если сходится интеграл
в том случае, если сходится интеграл  - это
- это
расходящийся несобственный интеграл
сходящийся несобственный интеграл
абсолютно сходящийся несобственный интеграл
абсолютно расходящийся несобственный интеграл
Интегралом Фурье функции f(x)=x называется выражение вида
x =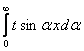
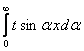
x =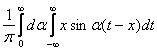
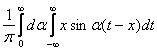
x =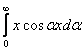
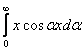
x =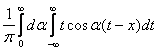
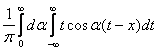
Выражение 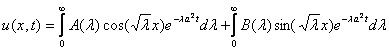 , где
, где 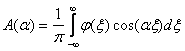 ,
, 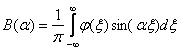 , является решением задачи Коши для уравнения
, является решением задачи Коши для уравнения
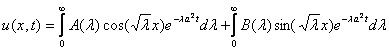 , где
, где 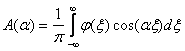 ,
, 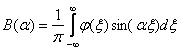 , является решением задачи Коши для уравнения
, является решением задачи Коши для уравнениятеплопроводности
Лапласа
Пуассона
волнового
Верны ли утверждения? А) Для определения обратного преобразования от произведения Фурье–образов, надо найти прообразы каждого из сомножителей, то есть функции 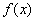 и
и 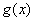 , а затем вычислить их свертку. Б) Интегральным преобразованием называют преобразование, которое каждой функции
, а затем вычислить их свертку. Б) Интегральным преобразованием называют преобразование, которое каждой функции 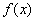 ставит в соответствие новую функцию
ставит в соответствие новую функцию 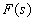 по формуле
по формуле 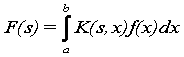
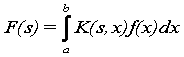
А - нет, Б - нет
А - нет, Б - да
А – да, Б - да
А - да, Б - нет
Решение задачи Коши для уравнения теплопроводности Ut = 9Uxx с начальным условием U(x,0) = j(x)= имеет вид
имеет вид
U(x,t) =3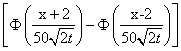
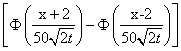
U(x,t) = 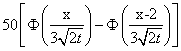
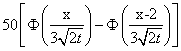
U(x,t) = 3

U(x,t) = 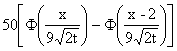
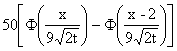
Коэффициент В(l) в задаче Коши для уравнения теплопроводности Ut = Uxx, U(x,0) = j(x) вычисляется по формуле В(l) = 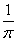
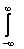 j(x)sinx
j(x)sinx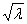 dxТогда коэффициент B(l) при U(x,0) = j(x) =
dxТогда коэффициент B(l) при U(x,0) = j(x) = 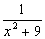 равен
равен
1
0
Верны ли утверждения? А) Преобразование Фурье - интегральное преобразование функций, задаваемое формулой F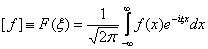 . Б) Интеграл Фурье функции
. Б) Интеграл Фурье функции 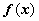 по косинусам - представление функции в виде
по косинусам - представление функции в виде 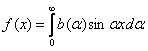 , где
, где 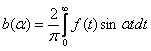
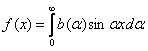 , где
, где 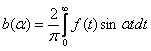
А – да, Б - да
А - нет, Б - нет
А - нет, Б - да
А - да, Б - нет
Если функция 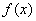 определена для всех
определена для всех 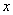 , то ей соответствует
, то ей соответствует 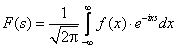 , которая для
, которая для 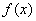 является ___ Фурье
является ___ Фурье
обратным преобразованием
ядром преобразования
ядром обратного преобразования
преобразованием
Решение задачи Коши для уравнения теплопроводности Ut = 4Uxx с начальным условием U(x,0) = j(x)= имеет вид
имеет вид
U(x,t) = 4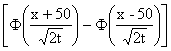
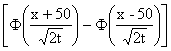
U(x,t) = 50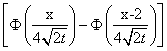
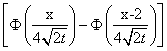
U(x,t) = 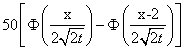
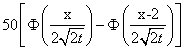
U(x,t) =2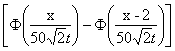 '
'
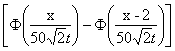 '
'Верны ли утверждения? А) Обратное интегральное преобразование - интегральное преобразование, которое восстанавливает первоначальную функцию из преобразованной Б) Ядро преобразования - функция 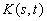 в интегральном преобразовании
в интегральном преобразовании
А – да, Б - да
А - да, Б - нет
А - нет, Б - да
А - нет, Б - нет
Интегральное преобразование функций, задаваемое формулой F-1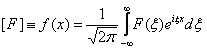 - это
- это
фундаментальное решение уравнения теплопроводности
формула Пуассона решения задачи Коши для уравнения теплопроводности
обратное преобразование Фурье
свертка функций
Cинус-преобразование Фурье функции f(x) записывается в виде: Fs(a) = 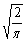
 f(x)sinax dx. Найти синус-преобразование Фурье функции
f(x)sinax dx. Найти синус-преобразование Фурье функции 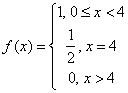
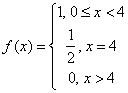
Функция 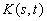 в интегральном преобразовании – это
в интегральном преобразовании – это
ядро преобразования
свертка функций
интеграл Фурье функции по косинусам
интеграл Фурье функции по синусам
_____________________________ - метод решения дифференциальных уравнений, который позволяет уменьшить число независимых переменных (по которым проводится дифференцирование), преобразуя некоторые переменные в параметры (по которым уже нет дифференцирования)
Метод преобразования Фурье
Метод интегральных преобразований
Метод дифференциальных преобразований
Метод разделения переменных
Верны ли утверждения? А) Пара преобразований Фурье 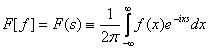 и
и 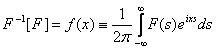 взаимно обратная, то есть для функции
взаимно обратная, то есть для функции 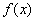 ,
,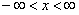 , выполняется тождество
, выполняется тождество 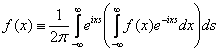 . Б) Преобразование Фурье – нелинейное преобразование
. Б) Преобразование Фурье – нелинейное преобразование
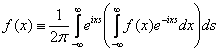 . Б) Преобразование Фурье – нелинейное преобразование
. Б) Преобразование Фурье – нелинейное преобразованиеА - нет, Б - да
А - да, Б - нет
А - нет, Б - нет
А – да, Б - да
Выражение 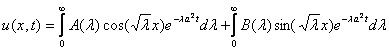 является решением задачи Коши для уравнения теплопроводности, где А и B равны
является решением задачи Коши для уравнения теплопроводности, где А и B равны
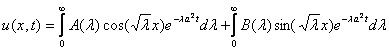 является решением задачи Коши для уравнения теплопроводности, где А и B равны
является решением задачи Коши для уравнения теплопроводности, где А и B равны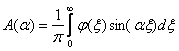 ,
, 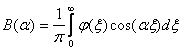
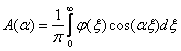 ,
, 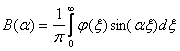
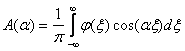 ,
, 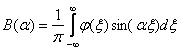
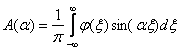 ,
, 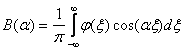
Верны ли утверждения? А) Точечный тепловой импульс - идеализация физического теплового импульса 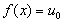 при
при 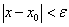 , если
, если 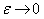 и
и 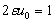 . Б) Фундаментальное решение уравнения теплопроводности - функция вида
. Б) Фундаментальное решение уравнения теплопроводности - функция вида 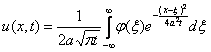 , которая при всех
, которая при всех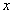 и
и 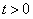 является решением задачи Коши для уравнения теплопроводности
является решением задачи Коши для уравнения теплопроводности
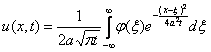 , которая при всех
, которая при всехА - да, Б - нет
А – да, Б - да
А - нет, Б - да
А - нет, Б - нет
Косинус-преобразование Фурье функции f(x) записывается в виде: Fc(a) = 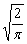
 f(x)cosax dx. Найти косинус-преобразование Фурье функции
f(x)cosax dx. Найти косинус-преобразование Фурье функции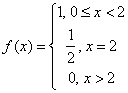
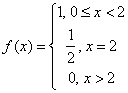
Задача Коши для уравнения теплопроводности имеет вид
Интегралом Фурье функции cos x называется выражение вида
cos x=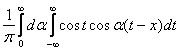
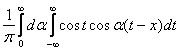
cos x=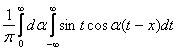
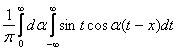
cos x=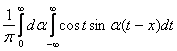
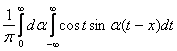
cos x=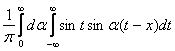
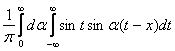
Преобразование Фурье F[f] по х функции f(x,t) имеет свойство
F[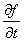 ] = is F[f]
] = is F[f]
F[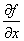 ] =
] = 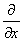 F[f]
F[f]
F[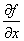 ] =
] = 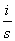 F[f]
F[f]
F[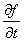 ] =
] = 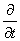 F[f]
F[f]
Выражение вида f(x) =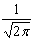
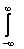 F(s)eixsds называется _____ Фурье
F(s)eixsds называется _____ Фурье
обратным преобразованием
коэффициентом
интегралом
разложением
Интегральное преобразование двух функций 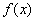 и
и 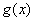 , задаваемое формулой
, задаваемое формулой 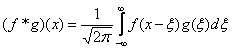 - это
- это
формула Пуассона решения задачи Коши для уравнения теплопроводности
свертка функций
фундаментальное решение уравнения теплопроводности
обратное преобразование Фурье
Верны ли утверждения? А) С каждым прямым преобразованием Фурье связано обратное преобразование, которое должно восстанавливать первоначальную функцию из преобразованной, то есть всегда возникает пара взаимно обратных преобразований Б) Обратное преобразование Фурье определяется формулой 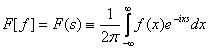
А - нет, Б - да
А - да, Б - нет
А - нет, Б - нет
А – да, Б - да
Верны ли утверждения? А) Сверткой 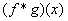 функций
функций 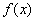 и
и 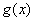 ,
,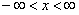 , называется функция, определяемая по формуле
, называется функция, определяемая по формуле 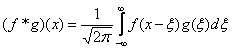 . Б) Метод Фурье-преобразования неудобен для решения линейных дифференциальных уравнений с постоянными коэффициентами
. Б) Метод Фурье-преобразования неудобен для решения линейных дифференциальных уравнений с постоянными коэффициентами
А - да, Б - нет
А - нет, Б - нет
А – да, Б - да
А - нет, Б - да
Функция 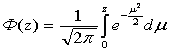 - это
- это
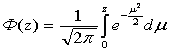 - это
- этофункция Лапласа
кривая Гаусса
функция Хэвисайда
фурье-изображение
Интегралом Фурье по синусам функции f(x) называется выражение вида
f(x)=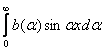
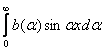
f(x)=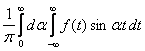
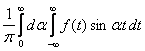
cos x=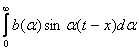
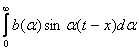
f(x)=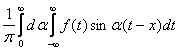
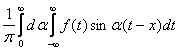
Верны ли утверждения? А) Несобственный интеграл 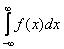 называется абсолютно сходящимся, если сходится интеграл
называется абсолютно сходящимся, если сходится интеграл  Б) Интегральным преобразованием называют преобразование, которое каждой функции
Б) Интегральным преобразованием называют преобразование, которое каждой функции 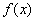 ставит в соответствие новую функцию
ставит в соответствие новую функцию 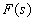 по формуле
по формуле 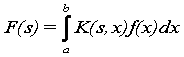
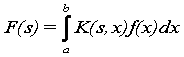
А - да, Б - нет
А - нет, Б - нет
А - нет, Б - да
А – да, Б - да
Верны ли утверждения? А) Интегральным преобразованием называют преобразование, которое каждой функции 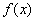 ставит в соответствие новую функцию
ставит в соответствие новую функцию 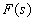 по формуле
по формуле 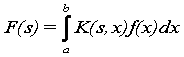 Б) Обратное преобразование Фурье определяется формулой
Б) Обратное преобразование Фурье определяется формулой 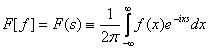
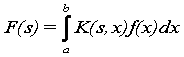 Б) Обратное преобразование Фурье определяется формулой
Б) Обратное преобразование Фурье определяется формулой А - да, Б - нет
А – да, Б - да
А - нет, Б - нет
А - нет, Б - да