Теория вероятностей, математическая статистика и случайные процессы
Вероятность стрелку попасть в мишень равна 0,9. Стрелок стреляет два раза. Р2 – вероятность попасть оба раза. Р1 – вероятность попасть один раз. Р0 – вероятность оба раза смазать
Р0
0,18
Р2
0,81
Р1
0,01
В тире лежат два ружья. Вероятность стрелку попасть из первого ружья 0,9. Вероятность стрелку попасть из второго ружья 0,6. Стрелок заходит в тир, первое ружьё берёт с вероятностью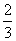 
, второе ружьё берёт с вероятностью
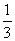, два раза стреляет. Р0 – вероятность, что попаданий нет. Р1 – вероятность, что попал один раз. Р2 – вероятность двух попаданий
, второе ружьё берёт с вероятностью, два раза стреляет. Р0 – вероятность, что попаданий нет. Р1 – вероятность, что попал один раз. Р2 – вероятность двух попаданийР0
0,66
Р1
0,28
Р2
0,06
Пусть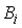 
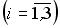- события, заключающиеся в том, что произошел обрыв в цепи сопротивлений 
, 
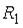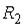или 
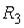
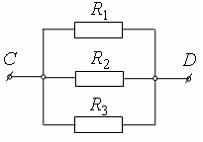Событие 
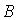- за время 
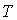произошел обрыв в электрической цепи между точкам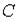и 
и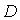 
. Тогда 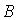представимо через 
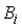следующим образом …
- события, заключающиеся в том, что произошел обрыв в цепи сопротивлений , или Событие - за время произошел обрыв в электрической цепи между точками и . Тогда представимо через следующим образом …
Вероятность наступления некоторого события не может быть равна
0
1,8
0,8
1
Среднеквадратическое отклонение суммы случайной величины Х и постоянной С равно:
σ(X + C) = σ(X)
σ(X + C) =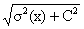 
σ(X + C) = σ(X) + C
σ(X + C) = C×σ(X)
Выберите верные утверждения
= 1
= 
= n,= n - 1Стрелок попадает в цель с вероятностью 0,5. Стрелок стреляет три раза. Р3 – вероятность попасть три раза. Р2 – вероятность попасть два раза, один раз смазать. Р1 – вероятность попасть один раз, два раза смазать. Р0 – вероятность все три раза смазать. Выберите верные утверждения
Р2 = 0,375
Р0 = 0,475
Р3 = 0,125
Р1 = 0,1
Случайная величина Х имеет биномиальное распределение с параметрами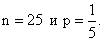 
Ее числовые характеристики таковы:
Ее числовые характеристики таковы:MX = 5; DX = 5
MX = 5; DX = 4
MX = 1; DX = 4
MX = 1; DX = 25
Вероятность стрелку попасть в мишень равна 0,9. Стрелок стреляет три раза. Р2 – вероятность попасть два раза. Р1 – вероятность попасть один раз. Р0 – вероятность ни разу не попасть
Р0
0,027
Р2
0,243
Р1
0,001
Вероятность появления события А в 10 независимых испытаниях, проводимых по схеме Бернулли, равна 0,7. Тогда дисперсия числа появлений этого события равна
2,1
0,21
0,07
7