Теория вероятностей, математическая статистика и случайные процессы
Дисперсия случайной величины обладает свойствами
DX = (MX)2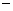
MX2
MX2DX = MX2 – (MX)2
DX = (MX)2
DX = MX2
В урне находятся 2 белых и 4 черных шара. Из урны поочередно вынимают два шара, но после первого вынимания шар возвращается в урну, и шары в урне перемешиваются. Тогда вероятность того, что оба шара белые, равна …
Вероятность наступления некоторого события не может быть равна
0,7
2,5
0,1
0
В электрическую цепь включены последовательно два прибора А и В.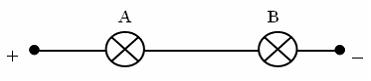 
При подаче напряжения прибор А сгорает с вероятностью 
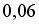, прибор В – с вероятностью 
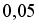. Считаем, что через сгоревший прибор ток не идёт. Тогда вероятность того, что при включении напряжения ток пройдёт через цепь, равна …
При подаче напряжения прибор А сгорает с вероятностью , прибор В – с вероятностью . Считаем, что через сгоревший прибор ток не идёт. Тогда вероятность того, что при включении напряжения ток пройдёт через цепь, равна …0,94
0,893
0,997
0,89
Выберите верные утверждения
5! = 30
6! = 720
3! = 3
4! = 24
Дискретная случайная величина Х имеет закон распределения вероятностей: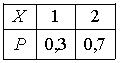 
. Математическое ожидание М(Х) этой случайной величины равно
. Математическое ожидание М(Х) этой случайной величины равно1,7
3
1
1,3
Формула полной вероятности имеет вид
P(A) =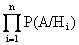 
P(A) =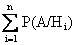 
P(A) =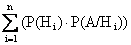 
P(A) = P(H1) + P(H2) + … + P(Hn)
Дискретная случайная величина Х задана законом распределения вероятностей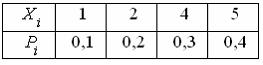 
Тогда значение интегральной функции распределения вероятностей 
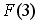равно …
Тогда значение интегральной функции распределения вероятностей равно …0,2
0,9
0,7
0,3
Вероятность появления события А в 20 независимых испытаниях, проводимых по схеме Бернулли, равна 0,9. Тогда дисперсия числа появлений этого события равна
1,8
0,45
0,18
18
Имеются две одинаковые на вид урны. В первой урне находятся два белых и один черный шар. Во второй урне – семь белых и семь черных шаров. Из наудачу взятой урны взяли один шар. Тогда вероятность того, что этот шар белый равна …
В первой урне 4 черных и 6 белых шаров. Во второй урне 3 белых и 7 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна…
0,45
0,15
0,9
0,4
Случайная величина Х имеет нормальное распределение с плотностью распределения f(x) =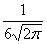 
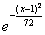. Тогда ее числовые характеристики МХ, DX и 
равны соответственно
. Тогда ее числовые характеристики МХ, DX и 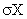равны соответственно36; 1: 6
6; 1; 1
1; 6; 36
1; 36; 6
Игральный кубик бросают один раз. Вероятность того, что на верхней грани выпадет число очков, равное трем или четырем, равна
1/2
2/3
1/3
1/6
Страхуется 1200 автомобилей; считается, что каждый из них может попасть в аварию с вероятностью 0.08. Для вычисления вероятности того, что количество аварий среди всех застрахованных автомобилей не превзойдет 100, следует использовать…
формулу полной вероятности
формулу Пуассона
интегральную формулу Муавра-Лапласа
формулу Байеса
Событие А может наступить лишь при условии появления одного из двух несовместных событий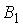 
и 
, образующих полную группу событий. Известны вероятность 
и условные вероятности 
. Тогда вероятность 
равна …
и 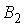, образующих полную группу событий. Известны вероятность 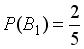и условные вероятности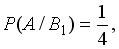 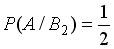. Тогда вероятность 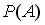равна …
В урне 4 билета. Из них 2 выигрышных. Вынимаем три билета случайным образом. Р3 – вероятность вынуть три выигрышных билета. Р2 – вероятность вынуть два выигрышных билета. Р1 – вероятность вынуть один выигрышный билет. Р0 – вероятность, что все билеты не выиграли. Выберите верные утверждения
Р0 = 0
Р3 = 0,1
Р1 = 0,4
Р2 = 0,5
Вероятность невозможного события равна…
1
– 1
0
0,01
График плотности распределения вероятностей непрерывной случайной величины Х, распределённой равномерно в интервале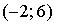 
, имеет вид: 
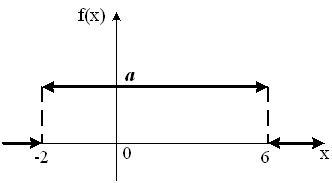Тогда значение a равно
, имеет вид: Тогда значение a равно1
Событие А может наступить лишь при условии появления одного из двух несовместных событий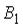 
и 
, образующих полную группу событий. Известны вероятность 
и условные вероятности 
. Тогда вероятность 
равна …
и 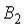, образующих полную группу событий. Известны вероятность 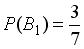и условные вероятности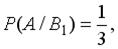 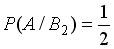. Тогда вероятность 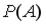равна …
Дисперсия случайной величины определяется по формуле
DX = (MX)3
DX = MX2
DX = M(X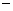MX)2
MX)2DX = (MX)2
Дисперсию случайной величины Y = aX + b, которая является линейной функцией от случайной величины Х, вычисляют по формуле
DY = a2×DX
DY = a2DX + b
DY = a×DX + b
DY = a×DX
Вероятность появления события А в 20 независимых испытаниях, проводимых по схеме Бернулли, равна 0,8. Тогда дисперсия числа появлений этого события равна
16
3,2
0,32
0,04
Вероятность наступления некоторого события не может быть равна
0,3
0
1,5
0,5
Область допустимых решений задачи линейного программирования имеет вид: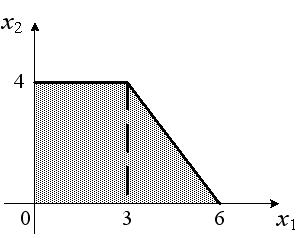 
34
20
27
32
Завод в среднем дает 27% продукции высшего сорта и 70% - первого сор та. Остальные изделия второго сорта. Найдите вероятность того, что наудачу взятое изделие будет второго сорта Ответ дайте десятичной дробью
Случайные события А и В, удовлетворяющие условиям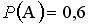 
, 
, 
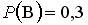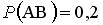, являются …
, , , являются …совместными и независимыми
несовместными и зависимыми
совместными и зависимыми
несовместными и независимыми
По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию, равны 0,1 и 0,35. Тогда вероятность банкротства обоих предприятий равна
0,35
0,585
0,45
0,035
Случайная величина Х распределена по нормальному закону, ее математическое ожидание равно нулю, а среднеквадратическое отклонение равно 20. Плотность распределения Х имеет вид
f(x) =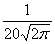 
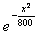
f(x) =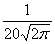 
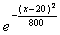
f(x) =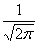 
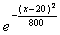
f(x) =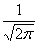
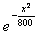
Вероятность наступления некоторого события не может быть равна
0,9
0,1
1,1
1
Выберите верные утверждения
= 10
= 10
= 2
= 0Имеются две одинаковые на вид урны. В первой урне находятся три красных и один черный шар. Во второй – два красных и один черный шар. Из наудачу взятой урны взяли один шар. Тогда вероятность того, что этот шар красный равна …
Вероятность невозможного события равна…
0,0002
1
– 1
0
Случайная величина Х распределена по нормальному закону, её плотность вероятности f(x) =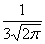 
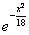. . Тогда ее МХ, DX и таковы
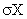. . Тогда ее МХ, DX и таковыMX = 3; DX = 0; σX = 0
MX = 0; DX = 9; σX = 3
MX = 0; DX = 3; σX = 9
MX = 3; DX = 3; σX = 9
График плотности распределения вероятностей непрерывной случайной величины Х, распределённой равномерно в интервале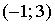 
, имеет вид: 
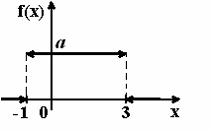Тогда значение а равно
, имеет вид: Тогда значение а равно1
0,25
0,2
0,33
Возможные значения случайной величины X таковы: x1 = 2, х2 = 5, x3 = 8. Известны вероятности: Р (X = 2) = 0.4; Р(X = 5) = 0.15. Найдите Р (X = 8). Ответ дайте десятичной дробью
В тире лежат два ружья. Вероятность стрелку попасть из первого ружья 0,7. Вероятность стрелку попасть из второго ружья 0,6. Стрелок заходит в тир, наугад берёт ружьё, два раза стреляет. Р0 – вероятность, что попаданий нет. Р1 – вероятность, что попал один раз. Р2 – вероятность двух попаданий
Р2
0,125
Р1
0,45
Р0
0,425
В урне 5 билетов. Из них 2 выигрышных. Вынимаем три билета случайным образом. Р3 – вероятность вынуть три выигрышных билета. Р2 – вероятность вынуть два выигрышных билета. Р1 – вероятность вынуть один выигрышный билет. Р0 – вероятность, что все билеты не выиграли. Выберите верные утверждения
Р2 = 0,3
Р1 = 0,2
Р3 = 0
Р0 = 0,2
Вероятность суммы двух случайных событий вычисляется по формуле
Р(А+2. = Р(1. + Р(2.
Р(А+2. = Р(1. + Р(2. – Р(А2.
Р(А+2. = Р(1.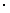 
Р(2.
Р(2.Р(А+2. = Р(1. + Р(В/1.
Дискретная случайная величина Х имеет закон распределения вероятностей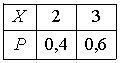 
Математическое ожидание М(Х) этой случайной величины равно
Математическое ожидание М(Х) этой случайной величины равно1
5
2,4
2,6
По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию, равны 0,2 и 0,35. Тогда вероятность банкротства обоих предприятий равна
0,7
0,55
0,07
0,52
Станок-автомат производит изделия трех сортов. Первого сорта - 80%, второго - 15%, остальные третьего сорта. Чему равна вероятность того, что наудачу взятое изделие будет или второго, или третьего сорта? Ответ дайте десятичной дробью
Из урны, в которой находятся 6 черных и 4 белых шаров, вынимают одновременно 2 шара. Тогда вероятность того, что оба шара будут черными, равна...
Случайная величина Х имеет биномиальное распределение с параметрами n = 20, p =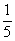 
тогда ее числовые характеристики:
тогда ее числовые характеристики:MX = 4; DX =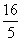 
MX = 4; DX =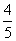 
MX = 1; DX =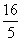
MX = 4; DX = 4
График плотности распределения вероятностей непрерывной случайной величины Х, распределённой равномерно в интервале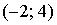 
, имеет вид: 
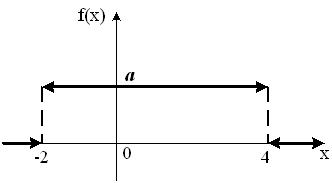Тогда значение a равно
, имеет вид: Тогда значение a равно
1
По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию, равны 0,2 и 0,05. Тогда вероятность банкротства обоих предприятий равна
0,1
0,76
0,25
0,01
Точечная оценка математического ожидания нормального распределения равна 16. Тогда его интервальная оценка может иметь вид...
(14,9; 16)
(14,9; 15,2)
(14,9; 17,1)
(16; 17,1)
Два стрелка стреляют по одной мишени. Вероятность попадания первым стрелком равна 0,9. Вероятность попадания вторым стрелком равна 0,8. Р2 – вероятность попасть обоим стрелкам. Р1 – вероятность, что попал только один стрелок. Р0 – вероятность смазать обоим стрелкам. Р0,1 – вероятность первый смазал, второй попал. Выберите верные утверждения
Р2 = 0,5
Р1 = 0,26
Р0,1 = 0,3
Р0 = 0,02
В урне лежит 3 белых и 2 черных шара. Последовательно, без возвращения и наудачу извлекают 3 шара. Тогда вероятность того, что первый шар будет белым, а второй и третий - черными, равна …
Вероятность наступления некоторого события не может быть равна
1
0,5
0,3
1,5
Два стрелка производят по одному выстрелу. Вероятность попадания в цель для первого и второго стрелков равны 0,6 и 0,9 соответственно. Тогда вероятность того, что цель будет поражена, равна …
0,996
0,96
0,46
0,54