Теория вероятностей, математическая статистика и случайные процессы
Имеются две одинаковые на вид урны. В первой урне находятся три белых, один красный и один черный шар. Во второй урне – два белых, один красный и два черных шара. Из наудачу взятой урны взяли одновременно два шара. Тогда вероятность того, что оба шара белые равна …
Бросают 2 монеты. События А – «цифра на первой монете» и В – «герб на второй монете» являются:
несовместными
независимыми
зависимыми
совместными
Дискретная случайная величина Х задана законом распределения вероятностей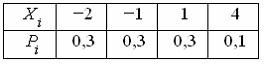 
Тогда значение интегральной функции распределения вероятностей 
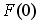равно …
Тогда значение интегральной функции распределения вероятностей равно …0,3
0,4
0,6
0,9
Случайная величина Х имеет биномиальное распределение с параметрами n = 4, p =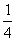 
тогда ее числовые характеристики
тогда ее числовые характеристикиMX =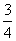 
; DX = 1
; DX = 1MX = 1; DX = 1
MX = 1; DX =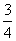
MX = 1; DX =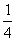
Стрелок попадает в цель с вероятностью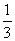 
. Стрелок стреляет три раза. Р3 – вероятность попасть три раза. Р2 – вероятность попасть два раза, один раз смазать. Р1 – вероятность попасть один раз, два раза смазать. Р0 – вероятность все три раза смазать. Выберите верные утверждения
. Стрелок стреляет три раза. Р3 – вероятность попасть три раза. Р2 – вероятность попасть два раза, один раз смазать. Р1 – вероятность попасть один раз, два раза смазать. Р0 – вероятность все три раза смазать. Выберите верные утвержденияР3 =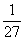 
Р1 =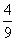 
Р2 =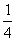
Р0 =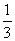
В урне 5 билетов. Из них 2 выигрышных. Вынимаем три билета случайным образом. Р3 – вероятность вынуть три выигрышных билета. Р2 – вероятность вынуть два выигрышных билета. Р1 – вероятность вынуть один выигрышный билет. Р0 – вероятность, что все билеты не выиграли. Выберите верные утверждения
Р3 = 0
Р2 = 0,2
Р1 = 0,2
Р0 = 0,1
Случайная величина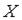 
распределена равномерно на отрезке 
. Тогда случайная величина 
имеет…
распределена равномерно на отрезке 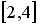. Тогда случайная величина 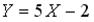имеет…равномерное распределение на отрезке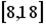 
равномерное распределение на отрезке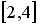
другой (не равномерный) вид распределения на отрезке
равномерное распределение на отрезке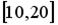 
Дискретная случайная величина Х задана законом распределения вероятностей: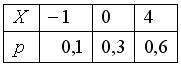 
Тогда математическое ожидание случайной величины 
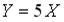равно…
Тогда математическое ожидание случайной величины равно…11,5
12,5
7,3
15
Дискретная случайная величина Х имеет закон распределения вероятностей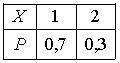 
Математическое ожидание М(Х) этой случайной величины равно
Математическое ожидание М(Х) этой случайной величины равно1,7
1
3
1,3
Укажите соответствие между формулами и их значениями
2
1
3
Случайная величина Х распределена по биномиальному закону с параметрами n = 10, p =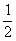 
. Ее числовые характеристики равны
. Ее числовые характеристики равныMX = 5; DX = 25
MX = 1; DX = 4
MX = 5; DX = 5
MX = 5; DX =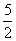 
Случайная величина Х распределена равномерно, ее плотность равна { f(x) =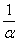 
при x Î [0,1]; f(x) = 0 при x Ï [0,1]}. Тогда параметр 
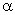равен
при x Î [0,1]; f(x) = 0 при x Ï [0,1]}. Тогда параметр равен1
2
0,2
0,5
Вероятность стрелку попасть в мишень равна 0,9. Стрелок стреляет четыре раза. Р2 – вероятность попасть точно два раза. Р3 – вероятность попасть точно три раза. Р4 – вероятность попасть точно четыре раза
Р3
0,0486
Р4
0,6561
Р2
0,2916
В урне 5 билетов. Из них 2 выигрышных. Вынимаем три билета случайным образом. Р3 – вероятность вынуть три выигрышных билета. Р2 – вероятность вынуть два выигрышных билета. Р1 – вероятность вынуть один выигрышный билет. Р0 – вероятность, что все билеты не выиграли. Выберите верные утверждения
Р2 = 0,3
Р3 = 0,2
Р1 = 0,6
Р0 = 0,2
График плотности распределения вероятностей непрерывной случайной величины Х, распределённой равномерно в интервале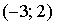 
, имеет вид: 
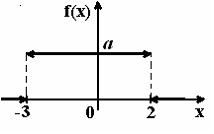Тогда значение а равно
, имеет вид: Тогда значение а равно0,4
1
0,25
0,2
График плотности распределения вероятностей непрерывной случайной величины Х, распределённой равномерно в интервале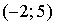 
, имеет вид: 
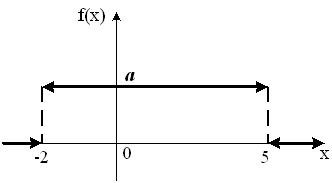Тогда значение a равно
, имеет вид: Тогда значение a равно
1
По мишени производится три выстрела. Значение вероятности ни одного попадания при всех трех выстрелах равно 0,5; значение вероятности ровно одного попадания - 0,3; значение вероятности ровно двух попаданий – 0,15. Тогда значение вероятности того, что мишень будет поражена не менее одного, но не более двух раз будет равно…
0,45
0,5
0,35
0,3
Два стрелка стреляют по одной мишени. Вероятность попадания первым стрелком равна 0,6. Вероятность попадания вторым стрелком равна 0,5. Р2 – вероятность попасть обоим стрелкам. Р1 – вероятность, что попал только один стрелок. Р0 – вероятность смазать обоим стрелкам. Р0,1 – вероятность первый смазал, второй попал. Выберите верные утверждения
Р0 = 0,2
Р1 = 0,5
Р0,1 = 0,3
Р2 = 0,4
Дана выборка объёма 10: 1,2,3,5,5,6,6,6,8,9 Выборочное среднее равно. Ответ дайте десятичной дробью
Укажите соответствие между формулами и их значениями
n
1
Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет 2 очка, равна…
0,2
Игральный кубик бросают один раз. Вероятность того, что на верхней грани выпадет число очков, меньшее чем три, равна
1/2
1/3
0
1
Вероятность невозможного события равна
1
– 1
0,001
0
Дискретная случайная величина Х имеет закон распределения вероятностей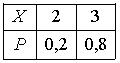 
. Математическое ожидание М(Х) этой случайной величины равно
. Математическое ожидание М(Х) этой случайной величины равно1
2,2
2,8
5
Дисперсия постоянной величины C равна
C
C2
0
Случайная величина Х равномерно распределена на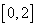 
, тогда ее математическое ожидание и дисперсия равны соответственно
, тогда ее математическое ожидание и дисперсия равны соответственно0, 2
, 12, 4
1,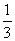
Выберите верные утверждения
= n×(n-1)
= 0= 
= 
Дискретная случайная величина задана законом распределения вероятностей 
Тогда вероятность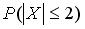 
равна …
Тогда вероятность равна …0,5
0,8
0,4
0,7
Два охотника одновременно стреляют в лису. Каждый охотник попадает в нее с вероятностью 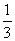. Вероятность того, что лиса будет подстрелена, равна
. Вероятность того, что лиса будет подстрелена, равна
1 –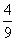
1
Случайная величина 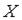распределена равномерно на отрезке 
. Тогда случайная величина 
имеет…
распределена равномерно на отрезке 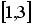. Тогда случайная величина 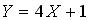имеет…равномерное распределение на отрезке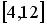 
другой (не равномерный) вид распределения
равномерное распределение на отрезке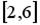 
равномерное распределение на отрезке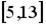 
Плотность распределения непрерывной случайной величины является
неположительной
неотрицательной
знакопеременной
ограниченной единицей
Выберите верные утверждения
4! = 4
2! = 2
1! = 1
3! = 3
Событие А может наступить лишь при условии появления одного из двух несовместных событи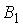й 
и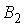 
, образующих полную группу событий. Известны вероятность 
и условные вероятности 
. Тогда вероятность 
равна …
и , образующих полную группу событий. Известны вероятность 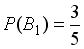и условные вероятности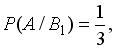 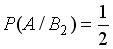. Тогда вероятность 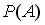равна …
По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию, равны 0,4 и 0,25. Тогда вероятность банкротства обоих предприятий равна
0,65
0,10
0,09
0,45
Рабочий обслуживает 3 станка. Вероятность того, что в течение часа станок потребует внимания рабочего, равна для первого станка 0,1, для второго 0,2 и для третьего 0,15. Найти вероятность того, что в течение некоторого часа хотя бы один из станков потребует внимания рабочего. Ответ дайте десятичной дробью
Вероятность появления события А в 10 независимых испытаниях, проводимых по схеме Бернулли, равна 0,4. Тогда дисперсия числа появлений этого события равна
2,4
4
0,04
0,24
Случайная величина распределена по нормальному закону, ее математическое ожидание равно 1, а дисперсия 25. Тогда ее функция распределения имеет вид
F(x) =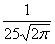 
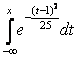
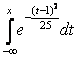
F(x) =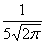 
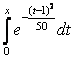
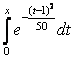
F(x) =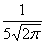 
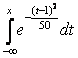
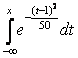
F(x) =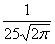
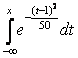
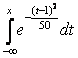
Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет 5 очков, равна…
0,1
DX = 1,5. Используя свойства дисперсии, найдите D(2X + 5). Ответ дайте числом
В первом ящике 7 красных и 9 синих шаров, во втором – 4 красных и 11 синих. Из произвольного ящика достают один шар. Вероятность того, что он синий, равна…
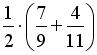
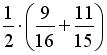
Вероятность наступления некоторого события не может быть равна
1
0,7
1,3
0,3
С первого станка на сборку поступает 60%, со второго – 40% всех деталей. Среди деталей первого станка 80% стандартных, второго – 70%. Взятая наудачу деталь оказалась стандартной. Тогда вероятность того, что она изготовлена на втором станке, равна …
В урне находятся 6 белых, 2 красных, 1 зеленый и 3 черных шара. Из урны поочередно вынимают три шара, но после первого вынимания шар возвращаются в урну. Тогда значение вероятности того, что все извлеченные шары белые, равно…
Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет более двух очков, равна…
MX = 1,5. Используя свойства математического ожидания, найдите M(2X+5). Ответ дайте числом
По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию, равны 0,4 и 0,05. Тогда вероятность банкротства обоих предприятий равна
0,20
0,57
0,02
0,45
Задана таблица распределения случайной величины. Найти р(X < 3). х 0 1 2 3 4 р 1/4 1/8 1/4 1/8 1/4 Ответ дайте числом в виде обыкновенной дроби a/b
Вероятность наступления некоторого события не может быть равна
0,5
2
1
0
Первый студент не сдаст сессию с вероятностью 0,2; а второй - с вероятностью 0,3. Вероятность того, что они оба не сдадут сессию, равна
0,5
0,05
0,6
0,06
Пусть X – дискретная случайная величина, заданная законом распределения вероятностей: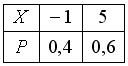 
Тогда математическое ожидание этой случайной величины равно…
Тогда математическое ожидание этой случайной величины равно…2
3
2,6
3,4