Математика (СП)
Площадь области, ограниченной линиями 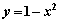
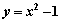 , вычисляют с помощью определенного интеграла
, вычисляют с помощью определенного интеграла
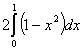 .
.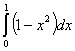
Для функции 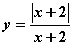 односторонние пределы в точке
односторонние пределы в точке 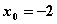 равны
равны
Объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями 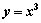 , х=1, х=0, равен
, х=1, х=0, равен
Множество 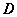 является областью определения функции
является областью определения функции 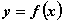 , а множество
, а множество 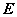 - областью значений этой функции. Областью определения функции
- областью значений этой функции. Областью определения функции 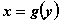 , обратной к данной является множество
, обратной к данной является множество
Объединение множеств 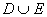
Площадь области, ограниченной линиями 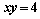
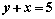 , вычисляют с помощью определенного интеграла
, вычисляют с помощью определенного интеграла
Наименьшее значение, монотонно убывающей на отрезке 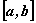 функции
функции 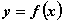 , равно
, равно
наименьшее значение функции не существует
Наибольшее значение, монотонно возрастающей на отрезке 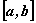 функции
функции 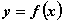 , равно
, равно
наибольшего значения функции не существует
Наименьшее значение, монотонно возрастающей на отрезке 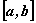 функции
функции 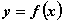 , равно
, равно
наименьшее значение функции не существует
Функция 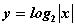 обладает следующими свойствами
обладает следующими свойствами
Область определения 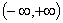 ; нечетная;
; нечетная; 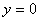 при
при 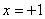 и
и 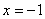
Область определения 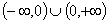 ; четная;
; четная; 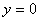 при
при 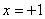 и
и 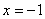
Область определения 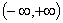 ; четная;
; четная; 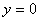 при
при 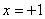 и
и 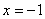
Область определения 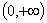 ; функция общего вида;
; функция общего вида; 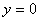 при
при 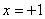 .
.
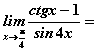
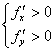
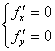
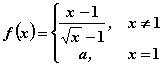 будет непрерывной при
будет непрерывной при