Математический анализ (курс 3)
Ряды 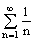 и
и 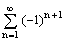
оба сходятся
первый - расходится, второй - сходится
первый - сходится, второй - расходится
оба расходятся
Ряд Фурье функции f(x) = -4х (-2 < x < 2), Т = 4 в точке х0 = 0 сходится к значению
расходится в точке х0 = 0
4
-4
0
Ряд Фурье функции f(x) = |х| (- p < x < p), Т = 2p, в точке х0 = -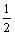 сходится к значению
сходится к значению
-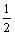
1
0
Ряд Маклорена функции у = cos 3x сходится
на всей числовой оси
только на интервале (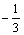 < x <
< x < 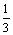 )
)
только на (-1,1)
только при х = 0
Ряд 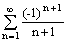
сходится условно
сходится абсолютно
расходится
сходится при четном n и расходится при нечетном n
Ряд 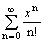 есть разложение функции
есть разложение функции
ln (1 + x) на промежутке -1 < x £ 1
ех только на интервале (-1,1)
sin x на всей числовой прямой
ех на всей числовой прямой
Разложение в ряд Маклорена функции у = cos x и область сходимости полученного ряда следующие:
Ряд Фурье функции f(x) = |х| (- p < x < p), Т = 2p, в точке х0 = 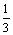 сходится к значению
сходится к значению
1
-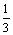
расходится в точке х0 = 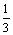
Ряд Фурье функции f(x) = х2 (- p < x £ p), Т = 2p, в точке х0 = 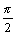 сходится к значению
сходится к значению
0
1
Ряд 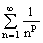 (р > 0)
(р > 0)
сходится при р £ 1
сходится при р > 1 и расходится при р £ 1
расходится при р > 1
сходится при всех р > 0
Ряд 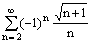
расходится
сходится абсолютно
сходится условно
расходится абсолютно
n-й коэффициент Фурье аn четной 2p-периодической функции f(x) вычисляется по формуле
аn= 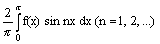
аn= 2p (n = 1, 2, ..)
an = 0 (n = 1, 2, …)
аn= 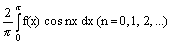
Ряд Фурье функции f(x) = х2 (-1< x < 1), Т = 2 в точке х0 = 1 сходится к значению
2
1
расходится в точке х0 = 1
0
Ряд Фурье функции f(x) = |х| (-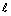 < x <
< x <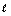 ), Т = 2ℓ, в точке х0 = 0 сходится к значению
), Т = 2ℓ, в точке х0 = 0 сходится к значению
0
-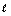
Ряд Фурье функции f(x) = |sin х| (-p < x < p), Т = 2p в точке х0 = 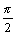 сходится к значению
сходится к значению
0
расходится в точке х0 = 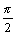
1
Ряд Маклорена для функции sin x и область сходимости следующие:
1 - 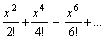 (-¥ < x < ¥)
(-¥ < x < ¥)
1 + 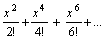 (-¥ < x < ¥)
(-¥ < x < ¥)
Коэффициент при х3 ряда Тейлора в окрестности точки х0 для функции f(x) равен
f’’(x0)
f(x0)
1
Ряд 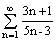
расходится, так как предел общего члена равен 5/3 и 5/3 < 1
сходится, так как предел общего члена равен 3/5 и 3/5 < 1
сходится, так как предел общего члена не равен нулю
расходится, так как не выполняется необходимый признак сходимости
Ряд Фурье функции f(x) = |х| (- p < x £ p), Т = 2p, в точке х = 0 сходится к значению
0
1
2p
Разложение в ряд Маклорена функции у = cos 4x и область сходимости полученного ряда следующие:
1 + х + х2 + х3 + … (-1 < x < 1)
1 + 2x + 4x2 + 6x3 + …(-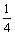 < x <
< x < 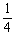 )
)
Ряд Фурье функции f(x) = |х| (-2 < x < 2), Т = 4, в точке х0 = 2 сходится к значению
4
расходится в точке х0 = 2
2
1
n-й коэффициент Фурье аn нечетной (n = 0, 1, 2, ..) 2p-периодической функции f(x) равен
1
2p
0
Ряд Фурье функции f(x) = х2 (-1< x < 1), Т = 2 в точке х0 = 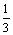 сходится к значению
сходится к значению
расходится в точке х0 = 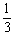
1
Ряд Маклорена для функции у = е3х сходится
на всей числовой прямой
только в промежутке (-1,1)
только при х = 1/3
только при х = 0
Коэффициент Фурье а1 для функции f(x) = х (- p < x £ p), Т = 2p равен
¥
0
1
-1
Радиус сходимости степенного ряда 1 + х + х2 + … + хn + … равен
-1
1
¥
0
Свободный член а0 ряда Фурье функции f(x) = 2х (-1 < x < 1), Т = 2 равен
0
2
-2
1
Ряды 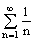 и
и 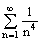
первый - расходится, второй - сходится
оба сходятся
оба расходятся
первый - сходится, второй - расходится
Ряд Фурье функции f(x) = |х| (- p < x < p), Т = 2p, в точке х0 = p сходится к значению
0
1
p
Разложение в ряд Маклорена функции у = sin 4x и область сходимости ряда следующие:
Ряд Фурье функции f(x) = 2х (-1 < x < 1), Т = 2 в точке х0 = -1 сходится к значению
1
0
расходится в точке х0 = -1
-1