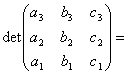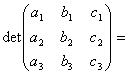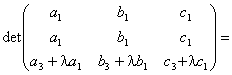Алгебра и геометрия (курс 1)
В линейной оболочке 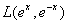 функции
функции 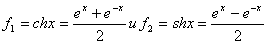 образуют базис. Координаты функции
образуют базис. Координаты функции 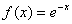 по этому базису равны:
по этому базису равны:
(1, -1)
(2, 2)
(1, 1)
(2, -2)
Любые четыре вектора в линейном арифметическом пространстве R3 _____________ зависимы
Координаты фокусов эллипса 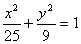 равны:
равны:
F1(-3, 0); F2(3, 0)
F1(-4, 0); F2(4, 0)
F1(-5, 0); F2(5, 0)
F1(0, -5); F2(0, 5)
Для матрицы 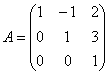 собственными числами являются:
собственными числами являются:
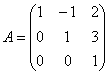 собственными числами являются:
собственными числами являются:только λ = 0
λ1 = λ2 = λ3 = 1
λ1 = λ2 = λ3 = -1
λ1 = 1, λ2 = -1, λ3 = 0
В пространстве R3 со стандартным скалярным произведением задан оператор А: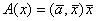 , где
, где 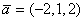 ,
, 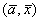 – скалярное произведение векторов
– скалярное произведение векторов 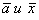 . Матрица оператора А в стандартном базисе
. Матрица оператора А в стандартном базисе 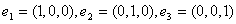 имеет вид:
имеет вид:
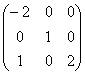
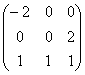
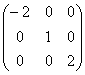
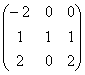
Квадратичная форма ______________ определена тогда и только тогда, когда все собственные числа ее матрицы не отрицательны.
Разложение по третьему столбцу определителя 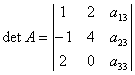 имеет вид:
имеет вид:
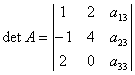 имеет вид:
имеет вид:-4a13 + 2a23 + 3a33
8a13 - 4a23 - 6a33
-8a13 + 4a23 + 6a33
4a13 - 2a23 - 3a33
Матрица 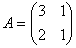 , Ã – матрица, составленная из алгебраических дополнений к элементам aij матрицы А. Укажите верные соответствия:
, Ã – матрица, составленная из алгебраических дополнений к элементам aij матрицы А. Укажите верные соответствия:
А Ã Т =
А-1 =
à =
Система векторов из R4 a̅1=(0,3,3,1), a̅2=(-1,1,0,-1), a̅3=(1,2,3,2):
линейно независима
линейно зависима
ранг системы равен 2
ранг системы равен 3
Прямые 14x - 7y + 5 = 0 и αx + y – 10 = 0:
при 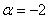 обе прямые перпендикулярны прямой
обе прямые перпендикулярны прямой 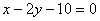
параллельны при 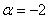
при 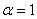 пересекаются в точке M (5, 5)
пересекаются в точке M (5, 5)
перпендикулярны при 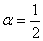
Укажите верные соответствия между матрицами А и обратными матрицами А-1
Уравнение высоты, опущенной из вершины B треугольника ABC с вершинами A (4, 1), B (2, 0), C(0, 5), имеет вид:
В пространстве многочленов степени n ≤ 2 задан оператор D: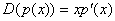 и многочлен
и многочлен 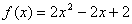 . Координаты образа D(f(x)) в базисе
. Координаты образа D(f(x)) в базисе 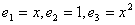 равны:
равны:
(0, 4, -2)
(4, -2, 0)
(-2, 0, 4)
(2, -2, 2)
________ называется геометрическое место точек плоскости, равноотстоящих от данной точки F и данной прямой.
Матрица А, все элементы которой равны нулю, называется _____________ матрицей.
Прямые x – 2y – 5 = 0 и 3x + 2y + 1 = 0 пресекаются в точке:
M(-1, -2)
M(1, -2)
M(-1, 2)
M(1, 2)
Вектор f = (1, –2) является собственным для матрицы 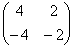 , отвечающим собственному значению:
, отвечающим собственному значению:
λ = -1
λ = 2
λ =1/2
λ = 0
Уравнение параболы с вершиной в точке А(-1, 0) и директрисой 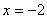 , имеет вид:
, имеет вид:
Ненулевой вектор x̅, который при умножении на квадратную матрицу А переходит в вектор Ax̅, коллинеарный вектору x̅, является _____________ вектором матрицы А
В линейной оболочке 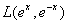 функция
функция 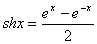 по базису
по базису 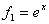 ,
, 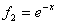 имеет координаты:
имеет координаты:
(1, -1)
(2, 2)
(2, -2)
Координаты фокусов гиперболы 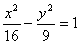 равны
равны
F1(-3, 0); F2(3, 0)
F1(-5, 0); F2(5, 0)
F1(-4, 0); F2(4, 0)
F1(0, -5); F2(0, 5)
Точки пересечения гиперболы с осями симметрии называются ______________ гиперболы.
Направляющим вектором прямой 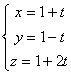 является вектор:
является вектор:
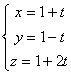 является вектор:
является вектор:s̅={-1,-1,-1}
s̅={1,-1,2}
s̅={1,1,1}
s̅={-1,1,-2}
В пространстве многочленов степени n ≤ 2 задан оператор дифференцирования 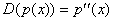 . Его матрица в стандартном базисе
. Его матрица в стандартном базисе 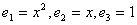 равна:
равна:
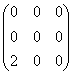
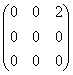
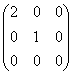
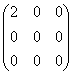
Уравнение параболы с вершиной в точке А(1, 0) и директрисой 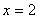 , имеет вид:
, имеет вид:
Уравнение 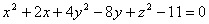 определяет эллипсоид с центром симметрии в точке:
определяет эллипсоид с центром симметрии в точке:
С(-1, 1, 0)
С(1, 1, 0)
С(-1) -1, 0)
С(1, -1, 0)
Направляющий вектор прямой 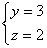 равен:
равен:
s̅={0,0,1}
s̅={1,0,0}
s̅={0,3,2}
s̅={0,1,0}
Установите верное соответствие между квадратичной формой и ее знаком
неотрицательно определенная
положительно определенная
знаконеопределенная
Даны векторы a̅=(1,0,1), b̅=(1,1,2), c̅=(1,2,3). Решением системы уравнений 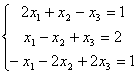 являются векторы:
являются векторы:
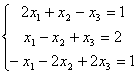 являются векторы:
являются векторы:ни один вектор не является решением системы
только вектор a̅
a̅, b̅, c̅
только вектор b̅
Острый угол j между векторами a̅={1,-1,0} и b̅={0,-1,1} равен ___º
0
60
30
45
Биссектриса I и III координатных углов и прямая, проходящая через точки А(1, 2) и В(0, 3):
перпендикулярны
пересекаются в точке В
пересекаются в точке А
параллельны
Определитель матрицы А порядка n ×n, полученный из матрицы А вычеркиванием i-ой строки и j-ого столбца, называется ________________ элемента aij.
Общее уравнение прямой, проходящей через точку М(1, 2) перпендикулярно прямой 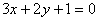 , имеет вид:
, имеет вид:
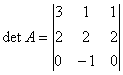 равен:
равен: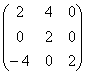
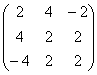
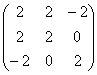
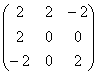
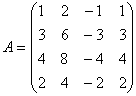 равен:
равен: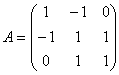 ,
, 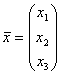 в координатной форме имеет вид:
в координатной форме имеет вид: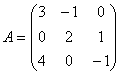 на вектор
на вектор 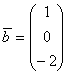 равно:
равно: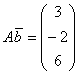
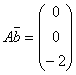
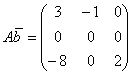
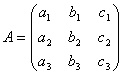 , det A = Δ.Укажите верные соответствия.
, det A = Δ.Укажите верные соответствия.