Выражения и множества их значений. Одночлены и многочлены. Уравнения и разложение многочленов на множители
В выражении аn число n — __________ степени
значением
показателем
основанием
выражением
Любое число можно представить в виде числа в степени
4
2
3
1
____________ называется сумма одночленов
Многочленом
Уравнением
Тождеством
Одночленом
Представьте в виде многочлена (3у+4)2
Множества двузначных чисел, кратных _____, – это 15, 30, 45, 60, 75, 90 (ответ указать числом)
___________ свойство множества - свойство, которым обладают все элементы этого множества и не обладают никакие другие объекты
Распределительное
Сочетательное
Основное
Характеристическое
Одночлены, из которых составлен многочлен, называют ___________ многочлена
элементами
членами
частями
выражениями
Упростите выражение и найдите его значение 6х2 - (7x2 - х) при x = 0,1
0,9
-0,09
0,09
0,99
Всякое двузначное число можно записать в виде _______, где а — цифра десятков, а b — цифра единиц
а + 10b
10а + b
10а + 10b
а + b
Запишите перечислением элементов, используя фигурные скобки, множество натуральных чисел, заключенных между числами 63 и 67
{64,65,66,67}
{63,64,65,66}
{63,64,65,66,67}
{64,65,66}
__________ степени - число в записи степени, показывающее, сколько раз основание степени повторяется в качестве множителя
Выражение
Показатель
Значение
Основание
Множество двузначных чисел, кратных 15, – это
{15, 30, 60, 75}
{15, 30, 45, 60, 75, 90}
{15, 30, 45, 60, 75, 90,105}
{ 30, 45, 60, 75, 90}
Число а в выражении а n называется
показателем степени
основанием степени
коэффициентом
степенью
Единый термин, употребляемый в целях единообразия для обозначения совокупностей, – это
Вынесите общий множитель за скобки у4 + у
у(у3)
у(у3+1)
у(у3-1)
-у(у3+1)
Представьте в виде произведения трех множителей многочлены6а2b + 14аb2 - 9а2с - 21аbс
а(3а-7b)(2b-3с)
а(3а+7b)(2b-3с)
а(3а+7b)(2b+3с)
а(3а-7b)(2b+3с)
Приведение подобных членов (слагаемых) многочлена – тождественное преобразование, состоящее в
сложении выражений с одинаковыми числами
сложении выражений с одинаковыми степенями
сложении выражений с одинаковыми буквами
замене суммы подобных членов многочлена одночленом
Установите соответствие
степень одночлена стандартного вида
степень тождественно равного ему многочлена стандартного вида
степень многочлена стандартного вида
наибольшая из степеней входящих в многочлен одночленов
степень произвольного многочлена
сумма показателей степеней входящих в него переменных
В одночлене -24а9b5 коэффициент равен
14
5
-24
9
_______ множество – множество, имеющее бесконечное число элементов
Решите уравнение 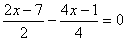
нет корней
0
1
2
___________ выражения - число, которое получается в результате выполнения действий в числовом выражении
__________ степени - число, которое в записи степени означает повторяющийся множитель
При деление одинаковых степеней с одинаковыми основаниями аn: аn получается
1
0
а
аn
Решите уравнение х3 - 8х2 + 3х - 24 = 0
2
8
4
–8
Вынесите общий множитель за скобки 7с4 - 9с2
-с2(7с2+9)
с2(7с2-9)
с2(7с2+9)
-с2(7с2-9)
Установите соответствие
а × 1 =
bа
а(bс) =
(аb)с
аb =
а
Решите уравнение 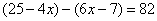
5
-6,4
-2,5
25
-5
Представьте одночлен 15х3у9 в виде произведения двух множителей, один из которых равен y5
15x3y4
15xy4
-15x3y4
15x3y3
Тождеством называется равенство, верное при _________ значениях переменных
любых допустимых
отрицательных
любых
положительных
Многочлен, состоящий из двух членов, называется
трехчленом
одночленом
двучленом
многочленом
Установите соответствие
элементы множества
одночлены, из которых составлен многочлен
четное число
свойство, которым обладают все элементы этого множества и не обладают никакие другие объекты
характеристическое свойство множества
число, которое делится на 2
члены многочлена
объекты или предметы, составляющие множество
Число а в степени 1 равно
1
0
а
3
Упростите выражение 7а+(-5b+3а)
10a-5b
0
10а+5b
5ab
Вынесите общий множитель за скобки b4 - b5
b4(1-b)
b4(b)
b4(-b)
b4(1+b)
Упростите выражение 2,4 (х2 - 1) - (0,6x - 1) (4x + 1)
3,4х+1,4
3,4х-1,4
-3,4х+1,4
-3,4х-1,4
Множество чисел обозначают буквой Q
Преобразуйте в многочлен выражения (х3 + у) (х2 - у2)
x5+y2 x3+yx2-y3
x5+y2 x3+yx2+y3
x5-y2 x3+yx2-y3
x5-y2 x3+yx2+y3
___________ свойство множества - свойство, которым обладают все элементы этого множества и не обладают никакие другие объекты
Преобразуйте в многочлен выражения (а3 - 26) (а – 4b2)
a4+4a3b2+26a+104b2
a4+4a3b2-26a+104b2
a4-4a3b2-26a+104b2
a4-4a3b2-26a-104b2
Если а — произвольное число, не равное нулю, n и m — любые натуральные числа, причем n > m, то аn : аm =
аn · m
аn : m
аn + m
аn - m
Разложите на множители 2а3 - 10а2 + 14а
2а(а2+5а+7)
2а(а2-5а-7)
2а(а2-5а+7)
2(а2-5а+7)
Представление многочлена в виде __________ двух или нескольких многочленов называют разложением многочлена на множители
суммы
произведения
разности
частного
Представьте в виде произведения трех множителей многочлены х2у - bх2 - аху + аbх
х(х+а)(у+b)
х(х-а)(у+b)
х(х+а)(у-b)
х(х-а)(у-b)
Запишите в виде выражения разность произведения чисел 37 и 6 и произведения чисел 29 и 5
(37-6)×(29-5)
37-6×29-5
37×6-29×5
37-6×29×5
В одночлене 12а6b4 коэффициент равен
4
12
6
10
Разложите на множители сумму 2х×(а - b) + у×(b - а)
(а+b) (2х +у)
(а-b) (2х -у)
(а-b) (2х +у)
(а+b) (2х -у)
Что называется степенью числа а с натуральным показателем n
любое число, квадрат которого равен а
произведение n множителей, каждый из которых равен а
натуральное число, полученное в результате выполнения действий
произведение а множителей, каждый из которых равен n
Найдите значение многочлена: 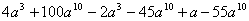 , где
, где 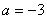
5315
-51
-57
57
51