Теория вероятностей и математическая статистика (курс 2)
В процедуре проверки гипотезы о виде распределения используется статистика 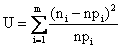 , которая имеет распределение
, которая имеет распределение
N(0,1)
Фишера-Снедекора
Стьюдента
χ2
Выборочное среднее 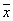 и выборочная дисперсия S2 для выборка объема n = 5: -6, -4, 0, 4, 6 равны
и выборочная дисперсия S2 для выборка объема n = 5: -6, -4, 0, 4, 6 равны
Для случайных величин 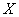 и
и 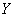 ковариация
ковариация 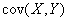 определяется как
определяется как
Некоррелированные случайные величины быть зависимыми
не могут
могут, т.к. всегда зависимы
могут при линейной связи между ними
могут
Оценка интенсивности потока обслуживания для N наблюдений одноканальной системы с неограниченной очередью, ui - число обслуженных требований, ui - число поступивших требований, 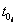 - общее время, когда система свободна за время наблюдения t, i - номер наблюдения; равна
- общее время, когда система свободна за время наблюдения t, i - номер наблюдения; равна
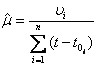
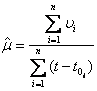
Для математического ожидания m стационарного случайного процесса, если известна реализация процесса x(t), при t Î [0; T], оценка 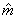 имеет вид
имеет вид
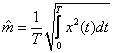
Абсолютная пропускная способность системы масcового обслуживания с неограниченной очередью, n - число каналов, l - интенсивность потока заявок, m - интенсивность потока обслуживания, r - загрузка системы, pn - вероятность того, что заняты все каналы и нет очереди; равна
A = r
A = m
A = l + m
A = l
Вероятность того, что в столбике из 150 наугад отобранных монет число монет, расположенных "гербом" вверх, будет от 50 до 75, может быть определена с помощью теоремы
Пуассона
Муавра-Лапласа
Чебышева
Маркова
Абсолютный момент случайной величины Х порядка n определяется выражением
В управляемом марковском процессе наибольший средний выигрыш достигается на стратегии
допустимой
наилучшей
принятой
оптимальной
Пусть 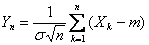 , где
, где 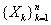 одинаково распределены и
одинаково распределены и 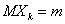 ,
, 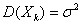 . Утверждение
. Утверждение 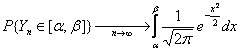
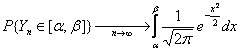
несправедливо
справедливо, если 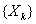 независимы
независимы
справедливо всегда
справедливо, если 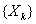 зависимы
зависимы
Плотности вероятностей перехода 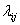 для однородного марковского процесса
для однородного марковского процесса
обладают свойством 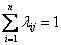
зависят от 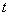
зависят от разности 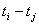 (для любых моментов времени)
(для любых моментов времени)
не зависят от 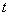
Абсолютная пропускная способность одноканальной системы с ограниченной очередью длиной m, интенсивностью потока заявок l, интенсивностью потока обслуживания m, загрузкой системы r и вероятностью p0 - того, что система свободна, и r - среднее число заявок в очереди, равна
A = 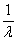 rm + 1p0
rm + 1p0
A = lrm + 1p0
A = l(1 - rm + 1p0)
A = 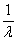 (1 - rm + 1p0)
(1 - rm + 1p0)
Выборочная медиана d для вариационного ряда выборки объема n = 9: -2, 0, 3, 3, 4, 5, 9, 11, 12 равна
4,5
3
5
4
Вероятность события А равна Р(А), вероятность противоположного события Р(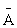 ) определяется как
) определяется как
1 - 2 Р(А)
2 Р(А)
1 - Р(А)
Три шарика случайным образом помещают в трех ящиках. Вероятность того, что в каждом ящике окажется по одному шарику, равна
Среднее число заявок r в одноканальной системе с ограниченной очередью длиной m, интенсивностью потока заявок l, нитенсивностью потока обслуживания m, загрузкой системы r и вероятностью p0 - того, что система свободна, равно
k = r + 1 - p0
k = r + 1 + p0
k = r - 1 - p0
k = r - 1 + p0
Вероятность для случайной величины X, распределенной «нормально с параметрами 3,2» - N[3,2], попасть внутрь интервала [-1,7] равна
0.9973
0.97
0.9544
0.68
Таблица частот по выборке объема 100 для проверки гипотезы о том, что генеральное распределение - равномерное на отрезке [0,1], имеет вид: Гипотеза о виде распределения по критерию Колмогорова ____________ на уровне значимости 0,05. Значение статистики, по которой оценивается мера расхождения, равно_______
Гипотеза о виде распределения по критерию Колмогорова ____________ на уровне значимости 0,05. Значение статистики, по которой оценивается мера расхождения, равно_______
 Гипотеза о виде распределения по критерию Колмогорова ____________ на уровне значимости 0,05. Значение статистики, по которой оценивается мера расхождения, равно_______
Гипотеза о виде распределения по критерию Колмогорова ____________ на уровне значимости 0,05. Значение статистики, по которой оценивается мера расхождения, равно_______проходит, 1
не проходит, 10
проходит, 10
не проходит, 1
Статистический (или эмпирический) начальный момент k-го порядка для выборки объема n: х1, х2, …, хn. находится по следующей формуле:
ak = 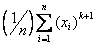
ak = 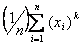
ak = 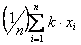
ak = 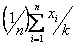
Дана выборка объема n: х1, х2, х3, …, хn. Ее выборочное среднее равно 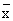 . Выборочная дисперсия находится по формуле
. Выборочная дисперсия находится по формуле
Дано статистическое распределение выборки: Выборочное среднее
Выборочное среднее 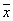 и выборочная дисперсия S2 равны
и выборочная дисперсия S2 равны
 Выборочное среднее
Выборочное среднее При проверке гипотезы об однородности двух выборок по критерию Колмогорова-Смирнова максимальная разница между эмпирическими распределениями оказалась равной 0,1. Число испытаний равно для обеих совокупностей n. Укажите значения n и вывод на уровне 0,05 о правильности гипотезы, не противоречащие друг другу:
n=200, гипотеза прoходит
n=500, гипотеза прoходит
n=100, гипотеза не прoходит
n=200, гипотеза не проходит
Производство дает 1,5% брака. Тогда вероятность того, что из взятых на исследование 1000 изделий выбраковано будет не больше 15, может быть определена с помощью теоремы
Муавра-Лапласа
Хинчина
Чебышева
Маркова
По выборке построена гистограмма. Медиана равна 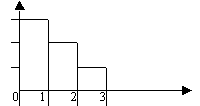

0
3
2
1
Из всех значений выборки для упрощения счета вычли 1280, при этом эмпирическая дисперсия
уменьшится на 1280
уменьшится в 1280 раз
увеличится в 1280 раз
не изменится
Электростанция обслуживает сеть, в которой 2000 ламп, вероятность включения каждой из них в зимний вечер равна 0,8. Вероятность того, что число одновременно включенных ламп будет более 1800, можно определить с помощью
теоремы Муавра-Лапласа
теоремы Хинчина
неравенства Чебышева
теоремы Пуассона
Всхожесть семян некоторого растения равна 0,8. Тогда вероятность того, что из 1000 посаженных семян число проросших будет заключено между 750 и 850, можно определить с помощью
теоремы Муавра-Лапласа
неравенства Чебышева
теоремы Маркова
теоремы Чебышева
Результат пяти измерений равен 1, результат трех измерений равен 2 и результат одного измерения равен 3. Выборочное среднее и выборочная дисперсия соответственно равны
≈4,67; 0,89
≈1,56; ≈0,47
2; 2,16
2; 0,17
Для стационарного случайного процесса при t = 0 ковариационная функция B(t) равна
периодической функции
постоянной величине
нулю
дисперсии этого процесса
Среднее время пребывания заявки в одноканальной системе с ограниченной очередью длиной m, интенсивностью потока заявок l, интенсивностью потока обслуживания m, загрузкой системы r и вероятностью p0 - того, что система свободна и r - среднее число заявок в очереди, равно
Вероятность того, что при бросании игральной кости один раз выпадает четное число очков, равна
0,6
0,4
0,35
Если из всех значений выборки для упрощения счета вычесть 1280, то эмпирическая дисперсия при этом
не изменится
уменьшится на 1280
увеличится в 1280 раз
уменьшится в 1280 раз
Статистика, с помощью которой по эмпирическому значению коэффициента корреляции r и числу испытаний n проверяется значимость коэффициента корреляции, имеет распределение
Фишера-Снедекора
χ2
нормальное
Стьюдента
Для случайной величины, имеющей плотность распределения 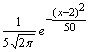 , математическое ожидание и дисперсия равны
, математическое ожидание и дисперсия равны
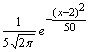 , математическое ожидание и дисперсия равны
, математическое ожидание и дисперсия равны2; 5
0; 5
2; 1
2; 25
В таблице статистического распределения, построенного по выборке, одна цифра написана неразборчиво.  Это цифра:
Это цифра:
 Это цифра:
Это цифра:х = 2
х = 3
х = 4
х = 5
Два охотника одновременно стреляют в лису. Каждый охотник попадает в нее с вероятностью 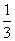 . Вероятность того, что лиса будет подстрелена, равна
. Вероятность того, что лиса будет подстрелена, равна
Формула для вычисления среднеквадратического отклонения дискретной случайной величины имеет вид
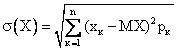
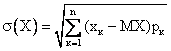
Правильным является следующее соотношение:
M(-2X) = -4M(X)
M(-2X) = -2M(X)
M(-2X) = 4M(X)
M(-2X) = 2M(X)
Для характеристических функций случайных величин 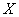 и
и 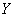 , где
, где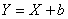 (
(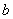 - число), формула
- число), формула 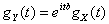
верна для 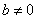
неверна
верна для 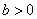
всегда справедлива
Закон распределения дискретного случайного вектора 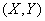 - это совокупность всех возможных значений данного вектора и вероятностей
- это совокупность всех возможных значений данного вектора и вероятностей 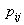 , равных
, равных
Сечение случайного процесса X(t) = j(t, w) получается при
фиксированных t = t0 и w = w0
фиксированном t = t0
фиксированном w = w0
вычислении математического ожидания
Доля обслуженных заявок среди поступивших в систему - это
интенсивность потока обслуживания
интенсивность потока заявок
относительная пропускная способность
абсолютная пропускная способность
Выборочная медиана d и выборочное среднее 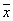 для вариационного ряда выборки объема n = 7: -5, -3, 0, 1, 1, 4, 16 равны
для вариационного ряда выборки объема n = 7: -5, -3, 0, 1, 1, 4, 16 равны
d = 1; 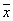 = 1
= 1
d = 5; 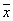 = 2
= 2
d = 2,5; 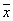 = 1
= 1
d = 1; 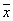 = 2
= 2
Выберите верное утверждение для случайных величин (X,Y):
если их коэффициент корреляции равен единице и они имеют нормальное распределение, то они независимы
если их коэффициент корреляции равен нулю, то они независимы
если их коэффициент корреляции равен нулю и они имеют нормальное распределение, то они независимы
если они независимы, то их коэффициент корреляции равен единице
Пусть случайные величины 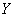 и
и 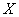 таковы, что
таковы, что 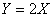 ,
,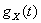 - характеристическая функция
- характеристическая функция 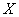 , тогда характеристическая функция
, тогда характеристическая функция 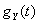 равна
равна
Возможна следующая таблица статистического распределения выборки
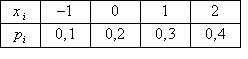
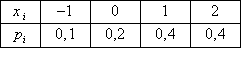
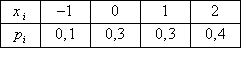
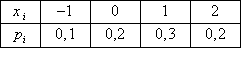
Случайная величина Х распределена по биномиальному закону с параметрами 
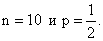 Ее числовые характеристики равны
Ее числовые характеристики равны
Случайный процесс - это
семейство случайных величин 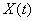 , где параметр
, где параметр 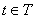 бесконечному множеству значений
бесконечному множеству значений
случайная функция, заданная на множестве целых чисел
семейство случайных величин 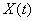 , где параметр
, где параметр 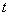 принимает конечное множество значений
принимает конечное множество значений
множество случайных функций