Теория вероятностей и математическая статистика (курс 2)
Уравнения Колмогорова позволяют найти
размеченный граф состояний системы
переходную матрицу
предельные вероятности состояний
вероятности состояний в марковском процессе
Если случайные величины 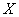 и
и 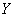 связаны линейной зависимостью
связаны линейной зависимостью 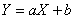 (где
(где 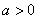 ,
, 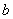 - любое), то коэффициент корреляции равен
- любое), то коэффициент корреляции равен
0
+1
-1
Для стационарного случайного процесса модуль ковариационной функции B(t) достигает при t = 0
любого промежуточного значения
наименьшего значения
наибольшего значения
нуля
Из 30 экзаменационных билетов студент хорошо выучил 8 «счастливых» билетов. Он вытаскивает один билет, тогда вероятность того, что билет будет счастливым, равна
Формула для определения ковариационной функции случайного процесса X(t) имеет вид
B(t, s) = cov[X(t), X(t + s)]
B(t, s) = cov[X(t - s), X(t + s)]
B(t, s) = cov[X(t), X(s)]
B(t, s) = cov[X(t), X(t)2]
Случайная величина имеет плотность распределения  Тогда параметр
Тогда параметр 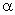 равен
равен
 Тогда параметр
Тогда параметр 2
3
1
Вероятность того, что карта, извлеченная из колоды в 32 , окажется красной масти, равна
Ряд распределения дискретной случайной величины Х - это
совокупность возможных значений случайной величины
сумма вероятностей возможных значений случайной величины
геометрическая интерпретация дискретной случайной величины
совокупность всех возможных значений случайной величины и их вероятностей
Числовые характеристики случайной величины Х, имеющей биномиальное распределение с параметрами 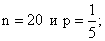 таковы:
таковы:
Вероятность того, что при бросании игральной кости один раз выпадает три очка, , равна
0,2
0,1
Выборочное среднее 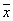 и выборочная дисперсия S2для выборки объема n = 5: 2, 3, 5, 7, 8 равны
и выборочная дисперсия S2для выборки объема n = 5: 2, 3, 5, 7, 8 равны
Вероятность того, что карта, извлеченная из колоды в 32, окажется тузом, равна
0,2
0,25
0,4
Пусть 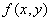 - плотность вероятности случайного вектора
- плотность вероятности случайного вектора 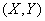 ,
, 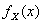 и
и 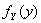 - плотности вероятностей координат этого вектора, причем
- плотности вероятностей координат этого вектора, причем 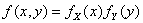 , тогда случайные величины
, тогда случайные величины 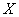 и
и 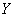
слабо зависимы
независимы
связаны линейно
зависимы
Для проверки гипотезы о равенстве 2-х генеральных средних надо пользоваться таблицами
пуассоновского распределения
плотности нормального распределения
распределения Стьюдента
нормального распределения
Коэффициент корреляции, полученный при проведении расчетов, равен
1,34
0,71
3,54
-1,22
Вероятность потерь по времени системы с отказами, где n - число пришедших требований, w - число потерянных требований среди пришедших, есть
Для вычисления полной вероятности следует воспользоваться формулой:
При проведении расчетов для дисперсионной модели от выборочных значений xij перешли к более удобным для расчета значениям yij=100xij - 30. Расчеты дали эмпирическое среднее по всем данным 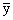 =3. Гипотеза о влиянии фактора на среднее значение не подтвердилась. В качестве оценки для генерального среднего можно взять значение
=3. Гипотеза о влиянии фактора на среднее значение не подтвердилась. В качестве оценки для генерального среднего можно взять значение
33
0,03
0,33
3,3
Оценка интенсивности потока обслуживания для одного наблюдения одноканальной системы с неограниченной очередью: t0 - общее время, когда система свободна, u - число обслуженных требований, а u - число требований, поступивших в систему за время наблюдения t; равна
Входящим потоком называется множество моментов
поступления требований в систему
окончания обслуживания поступивших требований
начала обслуживания поступивших требований
времени между поступлением и началом обслуживания требований
Возводятся два жилых дома. Вероятность сдачи в срок одного из них 0,8, а другого - 0,9. Тогда вероятность сдачи в срок хотя бы одного дома равна
0,6
Если вероятность появления успеха в каждом испытании равна 0,3, тогда вероятность наступления 75 успехов при 200 испытаниях может быть определена с помощью
теоремы Муавра-Лапласа
теоремы Маркова
теоремы Пуассона
неравенства Чебышева
Выборочное среднее 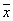 и выборочная дисперсия S2 для выборки объема n = 5: -2, -1, 1, 3, 4 равны
и выборочная дисперсия S2 для выборки объема n = 5: -2, -1, 1, 3, 4 равны
Величина x имеет распределение N(a, s). Вероятность p{x < a - 2s} равна
0,954
0,023
0,977
0,046
Среднеквадратическое отклонение определяется как
Числовые характеристики случайной величины Х, имеющей распределение Пуассона с параметром 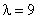 , равны
, равны
При исследовании корреляционной зависимости по данным 100 предприятий между капиталовложениями Х(млн. руб.) и выпуском продукции Y(млн. руб.) получены следующие уравнения регрессии: y=1,2x+2 и x=0,6y+2. Для аналогичных предприятий среднее значение для необходимого капиталовложения, чтобы получить выпуск продукции в 1млн. руб., составляет
3,6 млн. руб.
3,2 млн. руб.
2,6 млн. руб.
2,2 млн. руб.
В многоканальной системе массового обслуживания n каналов, длина очереди ограничена величиной m; загрузка системы - r; вероятность того, что система свободна, - p0; l и m соответственно интенсивности потока заявок и потока обслуживания. Относительная пропускная способность системы a равна
Хи-квадрат распределение с n степенями свободы - это функция распределения случайной величины 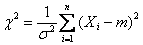 , где
, где 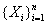 - независимые случайные величины, подчиненные одному и тому же закону
- независимые случайные величины, подчиненные одному и тому же закону
Эрланга
Пуассона с параметром 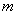
нормальному с параметрами 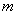 и
и 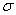
показательному с параметром 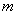
Мода и медиана случайной величины Х, имеющей нормальное распределение с плотностью 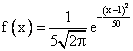 , равны соответственно
, равны соответственно
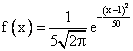 , равны соответственно
, равны соответственно5;5
1;5
1;1
5;1
Интенсивность потока заявок в системе массового обслуживания - это
доля обслуженных заявок среди поступивших
среднее число обслуженных заявок в единицу времени
среднее число заявок, приходящих в систему за единицу времени
число заявок, приходящих в систему за время ее работы
Среднее число занятых каналов системы с отказами и n каналами, интенсивностью потока заявок l, интенсивностью потока обслуживания m, загрузкой системы r, средним числом заявок в очереди r и вероятностью того, что система свободна p0, равно
Для корреляционной функции B(s) стационарного случайного процесса, если известна реализация процесса x(t) при t Î [0; T], оценка 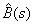 имеет вид
имеет вид
При проверке с помощью критерия χ2 гипотезы о равномерном распределении R(a,b), когда концы интервала a и b неизвестны, а число интервалов группировки равно m, статистика χ2 имеет распределение χ2 с числом степеней свободы
m - 3
m - 2
m - 1
m
Задачи управления марковскими процессами решаются с помощью уравнения
Беллмана
Лапласа
Фурье
Гаусса
Для однородных цепей Маркова матрица переходов
зависит от разности времен
не зависит от времени
не содержит нулевых элементов
имеет диагональный вид
Формула для вычисления условной вероятности события А при условии, что произошло событие В, имеет вид: Р(А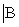 )=
)=
1 - Р(А)
1 - Р(В)
Формула для расчета случайной величины U, характеризующей степень расхождения теоретического и эмпирического закона распределения при проверке с помощью критерия χ2 нулевой гипотезы Н0 о том, что исследуемая случайная величина имеет определенный закон распределения, имеет вид
Если случайная величина 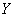 линейно зависит от случайной величины
линейно зависит от случайной величины 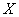 (
(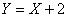 ), то коэффициент корреляции
), то коэффициент корреляции 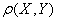 равен
равен
1
0
2
-1
Независимые случайные величины 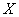 и
и 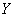 имеют соответственно характеристические функции
имеют соответственно характеристические функции 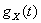 и
и 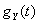 , тогда характеристическая функция их суммы
, тогда характеристическая функция их суммы 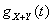 равна
равна
Плотность случайной величины Х, распределенной равномерно, равна 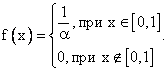 Тогда параметр
Тогда параметр 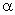 равен
равен
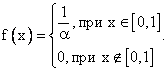 Тогда параметр
Тогда параметр 0,2
2
1
Для 2-х нормальных независимых величин с одинаковыми дисперсиями получены выборки объема nх = 42 и ny = 20 с такими характеристиками: 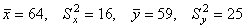 . При уровне значимости a=0.05 проверяется гипотеза о равенстве генеральных средних mx=my (конкурирующая гипотеза mx≠my). Опытное значение статистики Т, применяемой для проверки гипотезы Н0, равно
. При уровне значимости a=0.05 проверяется гипотеза о равенстве генеральных средних mx=my (конкурирующая гипотеза mx≠my). Опытное значение статистики Т, применяемой для проверки гипотезы Н0, равно
3.85
4.16
5.0
4.5
Пределы функции распределения F(x) на плюс и минус бесконечности равны соответственно
F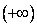 = 1, F
= 1, F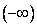 = 0
= 0
F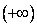 = 1, F
= 1, F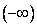 =
=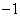
F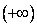 =
= 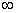 , F
, F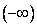 = 0
= 0
F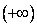 =
= 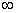 , F
, F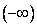 =
=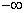
Пусть случайные величины 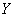 и
и 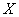 связаны зависимостью
связаны зависимостью 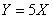 , тогда коэффициент корреляции
, тогда коэффициент корреляции 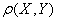 равен
равен
0
5
1
-1
Случайная величина распределена показательно с параметром 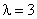 , тогда
, тогда 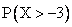 равна
равна
1
0
Если случайная величина имеет показательное распределение с параметром 2, тогда ее плотность распределения
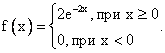
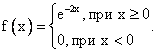
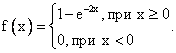
Ковариация B(t,s) случайного процесса X(t) = 3Vt, где V - случайная величина, имеющая стандартно нормальное распределение, равна
3(t + s)
9ts
3(t - s)2
3ts
Если случайная величина 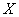 имеет математическое ожидание, равное нулю, и дисперсию - 1, тогда вероятность того, что величина
имеет математическое ожидание, равное нулю, и дисперсию - 1, тогда вероятность того, что величина 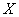 отклонится от нуля не меньше чем на 3, имеет оценку сверху
отклонится от нуля не меньше чем на 3, имеет оценку сверху
1/27
1/9
1
1/3
Выраженное через коэффициент корреляции r уравнение регрессии Y на Х имеет вид
По выборке построена таблица статистического распределения выборки. Из приведенных таблиц возможна следующая: