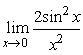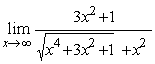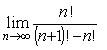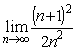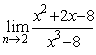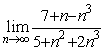Математический анализ (курс 6)
Последовательность может иметь
любое количество пределов
не больше двух разных пределв
два различных предела
только один предел
Во всех точках некоторого интервала ¦' (x) > 0. Тогда ¦(x) на этом интервале
убывает
монотонно не убывает
возрастает
не убывает
и 
Область определения функции y = x2, если известно, что x - сторона квадрата, а y - площадь этого квадрата, есть
вся числовая ось
интервал [0,+¥)
интервал (0, + ¥)
множество {x : x < + ¥}
Асимптотой графика функции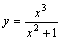 
будет прямая
будет прямаяy = - x
y = x
y = - x - 1
y = x + 1
Функция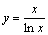 
на интервале (0, ¥)
на интервале (0, ¥)имеет минимум
имеет максимум
монотонно убывает
монотонно возрастает
a = ln (1 + 3x), b = arcsin 3x - две б.м. при x ® 0. Тогда они
эквивалентны
- высшего порядка
не сравнимы
одного порядка
Область определения функции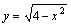 
есть
естьмножество {x : x ≤ 2}
интервал [0, 2]
интервал [-2, 2]
множество {x : x ≤ 4}
Полным дифференциалом функции z = ¦(x, y) в точке (x0, y0) называется
Частные приращения функции z = ¦(x, y) в точке P0 равны
Dxz и Dyz
Dxz = ¦(x0 + Dx, y0) - ¦(x0, y0), Dyz = ¦(x0 + Dx, y0 + Dy) - ¦(x0, y0)
Dxz = ¦(x0 + Dx, y0) - ¦(x0, y0), Dyz = ¦(x0, y0 + Dy) - ¦(x0, y0)
Dxz = ¦(x0 + Dx, y0), Dyz = ¦(x0, Dy) - ¦(x0, y0)
Функция ¦(x) называется нечетной, если
область определения функции симметрична относительной точки О
¦(- x) = - ¦(x) при всех x из области определения функции
формула для ¦(x) содержит только нечетные степени x
она не является четной
Производная функции ¦(x, y) = ln (x + y) в точке (1, 2) по направлению биссектрисы первого координатного угла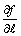 
равна
равна
Область значений функции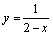 
есть
естьинтервал [ - 1, +¥)
{y : y ¹ 0}
интервал (- ¥, + ¥)
интервал (0, +¥)
Область определения функции y = log ½ (2x) есть
интервал [0, + ¥)
вся числовая ось, кроме x = 0
интервал (0, + ¥)
интервал (- ¥, + ¥)
. Тогда производная 
равна
. Тогда производная y' равна
Функция 
на интервале (0, 4)
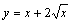на интервале (0, 4)монотонно убывает
имеет минимум
имеет максимум
монотонно возрастает
График функции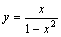 
имеет вертикальные асимптоты
имеет вертикальные асимптотыy = -1
y=-x
x = 1, x = - 1
y = 1
На интервале [a, b] непрерывная функция f (x) имеет единственную точку максимума c, a < c < b, и не имеет других точек экстремума. Ее наименьшее значение на [a, b] будет
при x = a
в критической точке
при x = b
либо ¦(a), либо ¦(b)
Наибольшая скорость возрастания функции ¦(x, y) = x2 - 2xy + 3y при переходе через точку (1, 2) равна
1
Коэффициенты A и B в формуле для полного приращения дифференцируемой в точке (x0, y0) функции z = ¦(x, y) равны
произвольные числа
A и B - б.м. высшего порядка относительно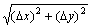 
Числовая ось - это прямая, на которой
выбрано начало отсчета, установлены направление и единица измерения длины
отсчитываются длины
выбрано начало отсчета
установлено направление
Интервалами монотонности функции y = |x| будут:
(- ¥, + ¥)
(0, + ¥) - возрастает
один интервал (- ¥, 0)
(- ¥, 0) - убывает и (0, + ¥) - возрастает
Градиент функции u = x2y2z2 в точке (1,2,3) равен
72 cos a + 36 cos b + 24 cos g
=(72,36,24)
2xy2z2 cos a + 2x2yz2 cos b + 2x2y2z cos g
Неявная функция задана уравнением ez - xyz = 0. Тогда частные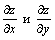 
производные соответственно равны
производные соответственно равны
Область значений функции y = |x| есть
интервал [0, + ¥)
вся числовая ось
интервал (- ¥, + ¥)
интервал (0, + ¥)
На интервале [a, b] непрерывная функция ¦(x) возрастает. Тогда ее наибольшее значение будет
¦(b)
в одной из критических точек
в точке экстремума
в некоторой точке c, a < c < b
Касательная плоскость к сфере x2 + y2 + z2 = 3 в точке (1, 1, 1) имеет уравнение
2x (x - 1) + 2y (y - 1) + 2z (z - 1) = 0
(x - 1) + (y - 1) + (z - 1) или x + y + z - 3 = 0
(x - 1) + (y - 1) = z - 1
z · (z - 1) = x (x - 1) + y (y - 1)
Если {an} - бесконечно малая последовательность и CÎRÞ {Сan} последовательность
малая
ограниченная
бесконечно большая
бесконечно малая
Производная функции ¦(x,y)=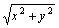
в точке (x0, y0) по направлению вектора 
равна
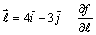в точке (x0, y0) по направлению вектора равна
Неявная функция задана уравнением x2+xy+y2=5. Тогда производная y’x равна
-x2-y2
x+2y
Уравнением нормали к поверхности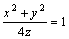 
в точке (2, 2, 2) является
в точке (2, 2, 2) являетсяx - 1 = y - 1 = 1 - z
x - 2 = y - 2 = 2 - z
x - 1 = y - 1 = z - 2
Функция y = x4 - 2x2 + 5 на интервале [-2, 0)
имеет минимум
монотонно убывает
монотонно возрастает
имеет максимум
{an} - бесконечно малая последовательность Þ
an=C(C-const)предел не существует
an=¥an=0Областью определения функции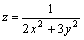 
является
являетсяточка (0, 0)
вся плоскость xOy, кроме точки (0, 0)
вся плоскость
{(x, y) : x > 0, y > 0}
z = x2 + 3y2 - 6x +5y. Экстремумом этой функции будет
единственная точка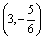 
- минимум
- минимумточка, где y" > 0
точка 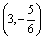- максимум
- максимумдве точки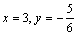 
Функция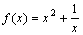 
не является четной потому, что
не является четной потому, чтосодержит нечетную степень x
определена не при всех x
является нечетной
¦(- x) ¹ ¦(x), например ¦(1) = 2, ¦(- 1) = 0
Областью определения функции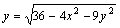 
является множество
является множествоточек {(x, y) : 4x2 + 9y2 ≤ 36}
(0, 0)
{(x, y) : - ¥ < x < + ¥, 0 < y < 2}
{(x, y) : x ≤ 3, - ¥ < y < ¥}
a = sin 2x, b = tg 5x.. При x® 0 эти б.м.
не сравнимы
более высокого порядка
одного порядка
эквивалентны
Область определения функции y = sin 2x есть
интервал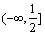 
интервал (- ¥, + ¥), т.е. вся числовая ось
интервал (- p, p)
интервал [0, + ¥)