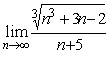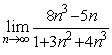Математический анализ (курс 6)
Последовательность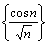 
является
являетсямалой
бесконечно большой
ограниченной
бескончно малой
Область определения функции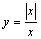 
есть
естьинтервал (- ¥, + ¥)
множество {x : x > 0}
множество {x : x ³ 0}
совокупность двух интервалов (- ¥, 0) и (0, + ¥), т.е. множество {x : x ¹ 0}
w = eyzx. Тогда частная производная второго порядка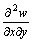 
равна
равнаxyz2eyz + zeyz
xyz2exyz + zexyz
xyzexyz + exyz
xyz2exyz
x и y - стороны прямоугольника, z = xy - его площадь. Областью определения функции является множество
{(x, y) : x > 0, y > 0}
{(x, y) : x ³ 0, y ³ 0}
вся плоскость, кроме точки O (0, 0)
вся плоскость
Областью определения функции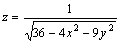 
является множество
является множество{(x, y) : 0 < x < 3, y < 2}
{(x, y) : - ¥ < x < + ¥, 0 < y < 2}
{(x, y) : 4x2 + 9y2 ≤ 36}
{(x, y) : 4x2 + 9y2 < 36}
Область значений функции 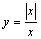состоит из
состоит издвух чисел y=-1 и y=1
множества всех чисел ¹ 0
интервалов (-¥,0) и (0,+¥)
интервала (-¥,+¥)
Область значений функции y =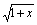
есть интервал
есть интервал(- ¥, + ¥)
- 1, +¥)
[0, + ¥)
(0, + ¥)
a и b - две б.м., причем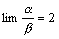 
. Тогда
. Тогдапорядок b выше
и b эквивалентны
более высокого порядка
и b одного порядка
Стационарными точками функции ¦(x, y) = x3 + ln3y - 3x ln y являются
(0; 1) и (1; е)
(- 1; 0) и (- 1; е)
(е; е) и (1; 1)
(1; 1) и (е; е)
Область определения функции y =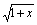есть
естьинтервал (- ¥, - 1)
интервал (- ¥, + ¥)
интервал [ - 1, + ¥)
интервал (- 1, + ¥)
Последовательность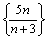 
бесконечно малая
бесконечно большая
ограниченная (½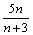
½£ 
)
½£ 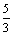)ограниченная (½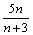½£ 5)
½£ 5)
=
a и b - две б.м. a высшего порядка в сравнении с b, если
, или 
еще меньше, чем b
Уравнением касательной плоскости к поверхности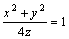 
в точке (2, 2, 2) является
в точке (2, 2, 2) являетсяx + y - z - 2 = 0
x - y + z + 2 = 0
x - y - z = 0
x - y - z - 2 = 0
Область значений функции y = ¦(x) есть
интервал оси Oy
ось Oy
множество всех значений, принимаемых величиной y
совокупность значений аргумента функции
Функция y = x4 - 2x2 + 5 на интервале (0, -2]
монотонно возрастает
имеет максимум
монотонно убывает
имеет минимум
. Тогда производная 
равна
y = cos (3x - 4). Тогда производная у’ равна
- sin (3x - 4)
- 3 sin (3x - 4)
3 cos (3x - 4)
- sinx · 3
имеет интервалов монотонности -
=
z = x3 - 2x2y +3y2. Тогда частные производные второго порядка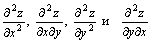 
соответственно равны
соответственно равны6x + 4y; 4x; 6; 4x
6x - 4y; - 4x; 6; - 4x
3x + 4y; - 2x; 6; - 2x
3x - 2y; 4x; 6y; 4x
Неявная функция задана уравнением x2 + y2 + z2 = 1. Тогда частная производная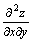 
равна
равна
Функция ¦(x) называется четной, если
область определения функции симметрична относительно точки О
¦(- x) = ¦(x) при всех x из области определения функции
область значений функции симметрична относительно точки О (на оси Oy)
формула для ¦(x) содержит только четные степени x
Область определения функции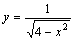 
есть
естьмножество {x : x > - 2}
интервал[- 2, + 2]
интервал (- 2 , + 2)
множество {x : x < 2}
График функции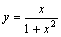 
асимптот (y) не имеет потому, что знаменатель не обращается в нуль
не имеет точек разрыва и, поэтому, асимптот
имеет единственную асимптоту: y = 0 (ось Ox) при x ® ± ¥
асимптот (y) не имеет
Если x и y- две переменные величины, причем lim x = a, lim y = b, то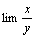 
есть
есть
не определен
, если b¹0не связан с a и b
Взаимно однозначное соответствие между точками числовой оси и действительными числами означает, что
каждая точка оси изображается действительным числом - своей координатой и каждое действительное число оказывается координатой определенной точки
все рациональные числа изображаются точками оси
все действительные числа лежат на оси
положительные и отрицательные целые числа являются координатами точек оси
Наибольшая скорость возрастания функции ¦(x,y)=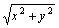
при переходе через точку (3, 4) равна
при переходе через точку (3, 4) равна
1
, 
. При x ® ¥ это две б.м., причемони не сравнимы
и b эквивалентны
высшего порядка, чем a
высшего порядка, чем b
У графика функции y = 3x3 - 2x2 + 6x - 1
функция возрастает
точки перегиба нет
критических точек для y" нет
точка перегиба есть - это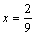 
Областью определения функции z = ln (xy) является множество
{(x, y) : xy ³ 0}
{(x, y) : x > 0, y > 0}
{(x, y) : xy > 0}
{(x, y) : xy > 1}
Во всех точках некоторого интервала ¦' (x) ≤ 0. Тогда ¦(x) на этом интервале
не возрастает
не убывает
убывает
монотонно убывает
Градиент функции u = x2 - y2 + sin z в произвольной точке равен
2x - 2y + cos z
2x cos a - 2y cos b + cos z cos g
Область определения функции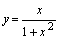 
есть
естьинтервал [ - 1, +¥)
интервал (- ¥, + ¥)
интервал ( - 1, +¥)
интервал (0, +¥)
Выражение dz = (y + 2x + 3y2)dx + (x + 6xy)dy является
вторым дифференциалом
градиентом
не полным дифференциалом
полным дифференциалом
Полное приращение функции z = ¦(x, y) в точке P0 (x0, y0) равно
¦(x0 + Dx, y0) - ¦(x0, y0)
¦(x0 + Dx, y0 + Dy) - ¦(x0, y0)
¦(x0 + Dx + Dy) - ¦(x0, y0)
¦(Dx, Dy) - ¦(x0, y0)