Алгебра (шк.об.). Первообразная и интеграл
Площадь фигуры, ограниченной графиками y=9x2-6x+1 y=0, x=0 и осями координат, вычисляется по формуле
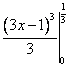
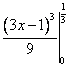
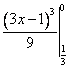
Общий вид первообразных для функции y=tg(-x)ctgx находится по формуле
-x+C
C
0
x+C
Для функции f(x)=4x3+2 первообразная, график которой проходит через точку М (1; 8), имеет вид
F(x)=х4+2х-5
F(x)=х4+2х+11
F(x)=х4+2х-11
F(x)=х4+2х+5
Для функции 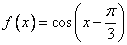 первообразная F, принимающая значение в указанной точке
первообразная F, принимающая значение в указанной точке 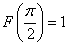 , имеет вид
, имеет вид
Прямолинейную трапецию ограничивают
отрезки параллельных оси Ох
перпендикулярные отрезки
отрезки прямых х=а и х=b
графики непрерывной и неотрицательной функции
Для функции f(x)=2+4x первообразная F, принимающая значение в указанной точке F(-1)=1, имеет вид
F(x)=2x2+2x+1
F(x)=2x2+2x
F(x)=2x2+2x-1
F(x)=4
Площадь криволинейной функции, с основанием [а;b] и ограниченной сверху графиком функции f(x) находится по формуле
F(b)·F(a)
F(b)-F(a)
а·b
Для функции 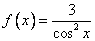 первообразная F, принимающая значение в указанной точке
первообразная F, принимающая значение в указанной точке 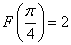 , имеет вид
, имеет вид
F(x)=3tgx+1
F(x)=3tgx-1
F(x)=3ctgx-1
F(x)=tgx+1
Для функции 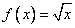 первообразная, график которой проходит через точку M (9; 10), имеет вид
первообразная, график которой проходит через точку M (9; 10), имеет вид
Площадь фигуры, ограниченной линиями y=x2+3, х=2, равна
48
Площадь фигуры, ограниченной линиями y= х-2, y=x2-4x+2, равна
9
4,5
3,5
Общий вид первообразных для функции y=sin2x-cos2x находится по формуле
sin2x+C
Если площадь заштрихованной фигуры представить как сумму или разность площадей криволинейных трапеций, ограниченных графиком известных вам линий, 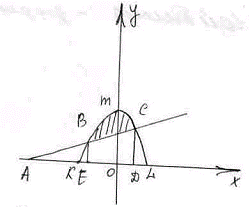 то она равна
то она равна
 то она равна
то она равнаS=SEBMCD-SEBCD
S=SACD+SBMC
S=SKBMCL-SEBCD
S=SKBMCL-(SKBE+SDCL)
Для функции f(x)=cosx первообразная, график которой проходит через точку 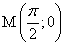 , имеет вид
, имеет вид
F(x)=-sinx+1
F(x)=-sinx
F(x)=sinx-1
Площадь фигуры, ограниченной графиками y=x2+1, y=0, x=0, x=1, вычисляется по формуле
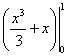
Площадь фигуры, ограниченной линиями y=x, y=2х, х=4, равна
2
6
8
4
Функция F(x)=2-sinx является первообразной для функции
f(x)=2x+cosx
f(x)=-cosx
f(x)=sinx+2x
f(x)=cosx
Общий вид первообразных для функции y=3sinx находится по формуле
3cosx+C
-3cosx+C
cosx+C
Площадь фигуры, ограниченной графиками y=x2-1, y=0, x=1, x=2, вычисляется по формуле
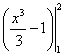
Зависимость скорости, движущейся прямолинейно, выражается формулой 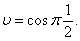 Координата точки в момент времени t=3,5, если при t=1 она равнялась 1, является
Координата точки в момент времени t=3,5, если при t=1 она равнялась 1, является
Функция F(x)=xcosx является первообразной для функции
f(x)=sinx
f(x)=sinx-cosx
f(x)=cosx-sinx
f(x)= -sinx
Общий вид первообразных для функции y=sin2x находится по формуле
 равен
равен10
12
24
26
Для функции 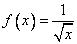 первообразная, график которой проходит через точку M (4; 4), имеет вид
первообразная, график которой проходит через точку M (4; 4), имеет вид
Площадь фигуры, ограниченной линиями y=cosx на отрезке 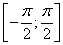 , равна
, равна
Общий вид первообразных для функции y=sin(-x)ctgx находится по формуле
-cosx+C
sinx+C
-sinx+C
cosx+C
Материальная точка движется со скоростью 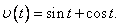 Уравнение движения точки, если при
Уравнение движения точки, если при 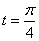 пройденный путь равен 3м, имеет вид
пройденный путь равен 3м, имеет вид
S(t)=-cost+sint+3
S(t)=cost+sint+3
S(t)=cost-sint-3
S(t)=-cost+sint-3
Если площадь заштрихованной фигуры представить как сумму или разность площадей криволинейных трапеций, ограниченных графиком известных вам линий, 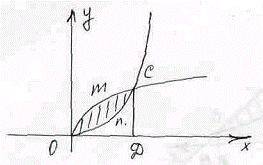 то она равна
то она равна
 то она равна
то она равнаS=SONCD-SOMCD
S=SOMCD-SONCD
S=SOMCN+SONCD
S=SOMCD+SONCD
Для функции 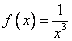 первообразная, график которой проходит через точку M (0,5; 3), имеет вид
первообразная, график которой проходит через точку M (0,5; 3), имеет вид
Для функции f(x)=x3 первообразная, график которой проходит через точку M (2; 1), имеет вид
С помощью интеграла 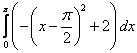 вычислена площадь фигуры, изображенной на рисунке
вычислена площадь фигуры, изображенной на рисунке 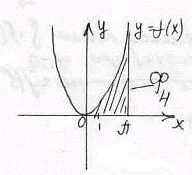
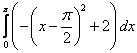 вычислена площадь фигуры, изображенной на рисунке
вычислена площадь фигуры, изображенной на рисунке 
Ф1
Ф2
Ф3
Ф4
Площадь фигуры, ограниченной линиями 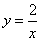 y=2x, x=3, равна
y=2x, x=3, равна
2ln3
8+2ln3
8
8-2ln3
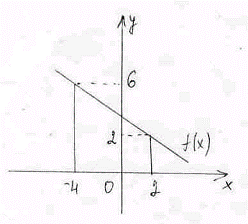
Площадь фигуры, заштрихованной на рисунке, 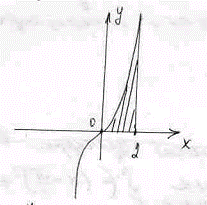 находится по формуле
находится по формуле
 находится по формуле
находится по формулеS=23
Площадь фигуры, ограниченной линиями 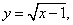 y=1, y =0, х=0, равна
y=1, y =0, х=0, равна
Общий вид первообразных для функции y=2sinxcosx находится по формуле
-cos2x+C
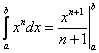
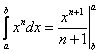
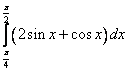 равен
равен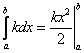
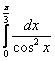 равен
равен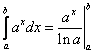
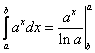
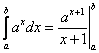
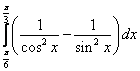 равен
равен