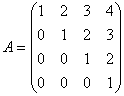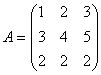Линейная алгебра. Часть 1
Квадратные матрицы А и В, для которых АВ = ВА, называются ____________________ (вставить слово)
Система линейных уравнений 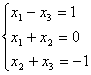 имеет:
имеет:
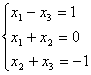 имеет:
имеет:общее решение 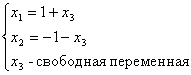
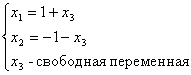
имеет два решения (1, -1, 0) и (0, 0, -1)
несовместна
имеет единственное решение 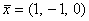
При перестановке двух строк определителя модуль определителя ________ (ответ словами)
Установите верные соответствия между матрицей А и матрицей Â, составленной из алгебраических дополнений к элементам матрицы А
Даны матрицы А и В: 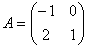 ,
, 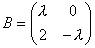 Матрица В является обратной к матрице А при
Матрица В является обратной к матрице А при 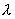 , равном:
, равном:
А - квадратная матрица второго порядка, В - матрица из алгебраических дополнений к элементам А: 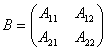 Тогда определитель (detB)2 равен:
Тогда определитель (detB)2 равен:
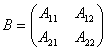 Тогда определитель (detB)2 равен:
Тогда определитель (detB)2 равен:detA
Если detA 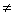 0, тогда:
0, тогда:
r(A) меньше порядка матрицы
система 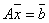 может быть решена методом Крамера
может быть решена методом Крамера
система 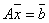 имеет единственное решение
имеет единственное решение
Матрицы 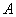 и
и 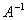 взаимно обратные. Тогда произведение (det
взаимно обратные. Тогда произведение (det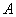 )(det
)(det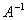 ) равно:
) равно:
зависит от определителя detA
зависит от порядка матрицы А
1
0
Все комплексные числа Z, для которых справедливо равенство 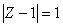 , на комплексной плоскости расположены на:
, на комплексной плоскости расположены на:
в точке (1, 1)
на оси ОХ в точках (1, 0) и (-1, 0)
окружности с центром в точке (1, 0) и радиусом R = 1
на оси OY в точках (0, 1) и (0, -1)
Матрица 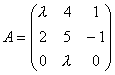 не имеет обратной при
не имеет обратной при 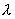 , равном:
, равном:
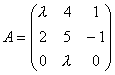 не имеет обратной при
не имеет обратной при 0 и -2
ни при каком 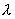
только при 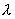 =0
=0
только при 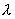 = -2
= -2
Если строки квадратной матрицы А линейно независимы, то:
detA 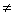 0
0
r(A) меньше порядка матрицы А
r(A) = n - числу строк матрицы
столбцы матрицы линейно зависимы
Система уравнений 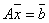 может быть решена по правилу Крамера тогда и только тогда, когда матрица А _________ матрица (вставить слово)
может быть решена по правилу Крамера тогда и только тогда, когда матрица А _________ матрица (вставить слово)
Фундаментальной системой решений называется ________ подпространства решений системы 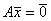 (слово)
(слово)
Даны матрицы А и В: 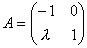 ,
, 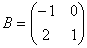 Матрицы А и В взаимно обратные при
Матрицы А и В взаимно обратные при 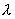 , равном:
, равном:
λ = 1
λ = -2
λ = 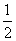
λ = 2
Максимальное число линейно независимых вектор-строк матрицы называется ее __________ (слово)
Система уравнений 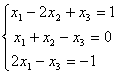 имеет:
имеет:
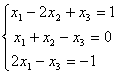 имеет:
имеет:множество решений
единственное решение
решением 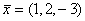
система несовместима
Множество решений системы линейных однородных уравнений 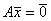 образует линейное ________ пространства Rn
образует линейное ________ пространства Rn
Укажите верные соответствия:
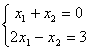
система несовместима
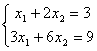
множество решений
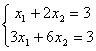
единственное решение
Элементарные преобразования над строками матрицы __________ ее ранга (ответ словами)
Система линейных уравнений совместима тогда и только тогда, когда ранг матрицы А __________ рангу расширенной матрицы 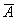 (вставить слово)
(вставить слово)
Общее решение уравнения с тремя неизвестными 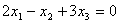 имеет вид:
имеет вид:
фундаментальная система решений состоит из 2-х векторов 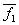 = (0, 0, 0),
= (0, 0, 0), 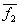 = (1, -1, -1)
= (1, -1, -1) 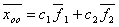
система имеет единственное нулевое решение 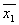 = (0, 0, 0)
= (0, 0, 0)
Общее решение системы линейных уравнений 
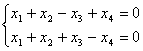 в векторной форме имеет вид:
в векторной форме имеет вид:
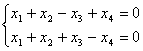 в векторной форме имеет вид:
в векторной форме имеет вид: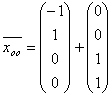
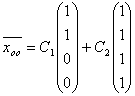
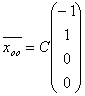
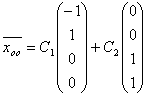
Значения переменной х, при котором многочлен f(x) обращается в нуль, называется ________ многочлена (вставить слово)
Общее решение системы линейных уравнений 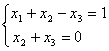 имеет вид:
имеет вид:
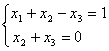 имеет вид:
имеет вид: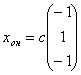 , с - константа
, с - константа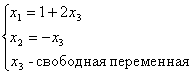
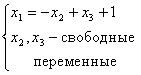
система несовместима
Основным точным методом решения системы линейных уравнений является метод _______ (вставьте название метод
Если detA = 0, тогда:
система 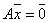 имеет подпространство решений
имеет подпространство решений
систему можно решить методом Крамера
система 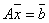 имеет единственное решение
имеет единственное решение
строки матрицы А линейно независимы
Все комплексные числа, расположенные на окружности, 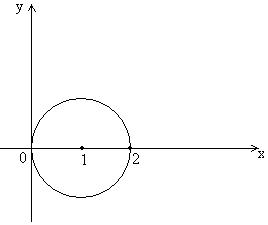 удовлетворяют условию:
удовлетворяют условию:
 удовлетворяют условию:
удовлетворяют условию:Даны матрицы 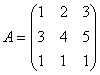 ,
, 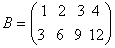 ,
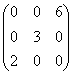
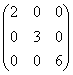
, 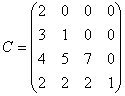 В порядке увеличения их рангов матрицы расположены так:
В порядке увеличения их рангов матрицы расположены так:
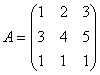 ,
, 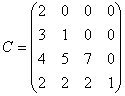 В порядке увеличения их рангов матрицы расположены так:
В порядке увеличения их рангов матрицы расположены так:А, В, С
ранги всех матриц равны
С, А, В
В, А, С
Если ранг матрицы системы уравнений 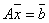 равен числу неизвестных, то:
равен числу неизвестных, то:
система имеет единственное решение
система несовместима
система имеет множество решений
число решений системы не определено
Дана система 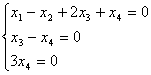 :
:
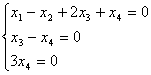 :
:система имеет только нулевое решение
размерность подпространства решений равна 1
фундаментальная система решений содержит один вектор
разномерность подпространства решений равна
Если для матрицы А системы уравнений и расширенной матрицы 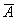 выполнено условие
выполнено условие 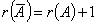 , то система уравнений _______ (вставить слово)
, то система уравнений _______ (вставить слово)
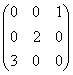 имеет вид:
имеет вид: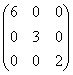
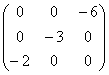
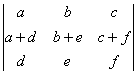 равен:
равен: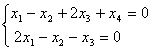 фундаментальной могут служить два вектора:
фундаментальной могут служить два вектора: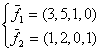
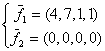
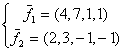
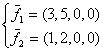
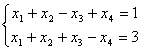 имеет вид:
имеет вид: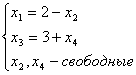
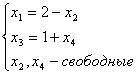
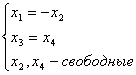
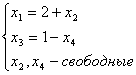
 равен:
равен: