Линейная алгебра. Часть 1
Если система уравнений 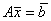 , где А - квадратная матрица может быть решена методом Крамера, то матрица А _______ (вставить слово)
, где А - квадратная матрица может быть решена методом Крамера, то матрица А _______ (вставить слово)
Дана матрица 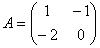 , вектор - столбец
, вектор - столбец 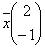 и вектор - строка
и вектор - строка 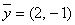 Укажите верные соответствия:
Укажите верные соответствия:
умножение невозможно
(4, - 2)
Даны матрицы А и В: 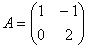 ,
, 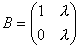 Матрица В является обратной к матрице А при
Матрица В является обратной к матрице А при 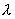 :
:
ни при каком 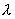
Установите верные соответствия между матрицей А и матрицей Â, составленной из алгебраических дополнений к элементам матрицы А
Все комплексные числа, расположенные на окружности, 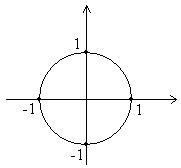 удовлетворяют условию:
удовлетворяют условию:
 удовлетворяют условию:
удовлетворяют условию:Система уравнений 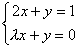 может быть решена методом Крамера при
может быть решена методом Крамера при 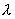 :
:
ни при каком значении 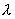
при любом 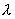
Ранг диагональной матрицы равен _________ ненулевых элементов ее главной диагонали (слово)
Общее решение системы 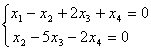 имеет вид:
имеет вид:
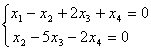 имеет вид:
имеет вид:система имеет только нулевое решение
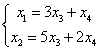 , х3, х4 - свободные переменные
, х3, х4 - свободные переменные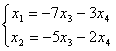 , х3, х4 - свободные переменные
, х3, х4 - свободные переменныесистема имеет единственное решение 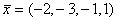
А - квадратная матрица второго порядка В - матрица из алгебраических дополнений к элементам А: 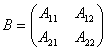 Тогда определитель detB равен:
Тогда определитель detB равен:
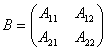 Тогда определитель detB равен:
Тогда определитель detB равен:detA
1
Матрица, определитель которой равен нулю, называется ____________ (вставьте слово)
Даны векторы 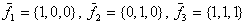 Базис в пространстве R3 можно составить из векторов:
Базис в пространстве R3 можно составить из векторов:
из векторов 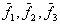 нельзя составить базис в
нельзя составить базис в 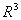
Чтобы для квадратной матрицы 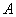 существовала обратная матрица
существовала обратная матрица 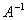 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы 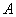 была _________ матрицей (вставить слово)
была _________ матрицей (вставить слово)
Система уравнений 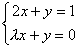 имеет единственное решение при значении
имеет единственное решение при значении 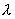 :
:
система имеет множество решений при любом 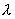
система несовместна при любом 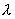
Дана матрица 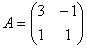 , вектор - столбец
, вектор - столбец 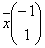 и вектор - строка
и вектор - строка 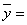 (0, 2) Укажите верные соответствия:
(0, 2) Укажите верные соответствия:
умножение невозможно
(2, 2)
Укажите верные соответствия для решения системы 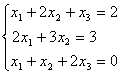 методом Крамера:
методом Крамера:
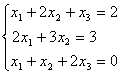 методом Крамера:
методом Крамера:х2 =
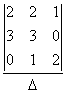
х3 =
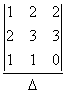
х1 =
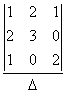
Одно уравнение с тремя неизвестными 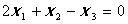 имеет решения в виде:
имеет решения в виде:
три решения: (0, 0, 0), (-1, 2, 0) и (-1, 0, 2)
подпространство V решений с размерностью 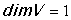
подпространство V решений, 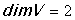
Матрица, составленная из алгебраических дополнений к диагональной матрице, является ________ матрицей (слово)
Одно уравнение с тремя неизвестными 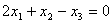 имеет:
имеет:
единственное тривиальное решение 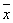 = (0, 0, 0)
= (0, 0, 0)
два решения 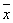 = (0, 0, 0) и
= (0, 0, 0) и 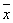 = (1, 1, 3)
= (1, 1, 3)
подпространство решений V и его размерность dimV = 2
множество решений, общий вид решения 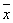 = С(1, 1, 3), где С - константа
= С(1, 1, 3), где С - константа
Дана система: 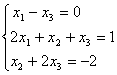 :
:
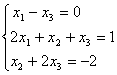 :
:общее решение системы имеет вид 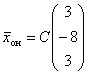
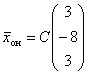
система имеет множество решений
система несовместима
система имеет единственное решение (3, -8, 3)
Однородное уравнение с тремя переменными 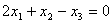 имеет решения в виде:
имеет решения в виде:
общее решение системы имеет вид 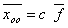 , где
, где 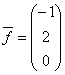
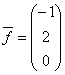
система имеет единственное решение 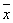 = (0, 0, 0)
= (0, 0, 0)
фундаментальная система решений состоит из одного вектора 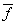 = (-1, 2, 0)
= (-1, 2, 0)
Если решением системы 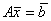 является вектор
является вектор 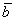 , то матрица А равна ________ (слово)
, то матрица А равна ________ (слово)
Если для квадратной матрицы А detA = 0, то:
r(A) равен числу столбцов матрицы
r(A) меньше порядка матрицы
столбцы матрицы линейно независимы
строки матрицы линейно зависимы
При транспонировании определитель ________________________ (что делает? Меняет знак или не изменяется Выберите верный ответ)
Система уравнений 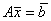 , где
, где 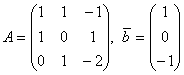 :
:
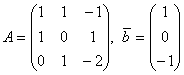 :
:имеет решение 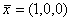
имеет решение 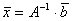
не может быть решена методом Крамера
несовместима
Система уравнений 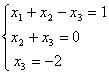 имеет:
имеет:
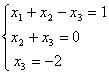 имеет:
имеет:единственное решение (-3, 2, -2)
единственное решение (3, 2, -2)
множество решений
система несовместима
Даны комплексно-сопряженные числа Z = a + bi и 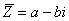 . Укажите верные соответствия
. Укажите верные соответствия
2bi
2a
Дан вектор - столбец 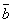 и матрица
и матрица 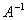 , обратная к матрице А:
, обратная к матрице А: 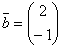 ,
, 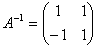 Тогда решением системы уравнений
Тогда решением системы уравнений 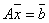 является вектор
является вектор 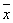 :
:
не зная матрицы А определить решение нельзя
С помощью элементарных преобразований Гаусса произвольную матрицу можно привести к _________ виду (вставить название теоремы)
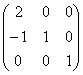 имеет вид:
имеет вид:
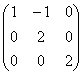
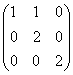
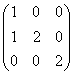
 равен:
равен: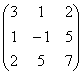
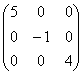
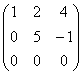
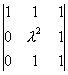 равен 0 при
равен 0 при 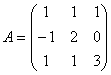 равен:
равен: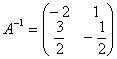
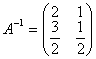
 = 0 при
= 0 при 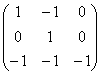 матрица из алгебраических дополнений имеет вид:
матрица из алгебраических дополнений имеет вид: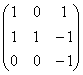
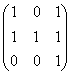
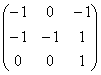
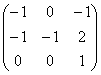
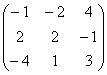 имеет вид:
имеет вид: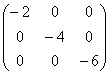

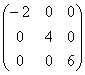
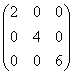
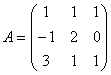 равен:
равен: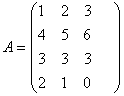 равен:
равен: