Аналитическая геометрия и линейная алгебра
Уравнение окружности 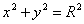 в полярной системе координат имеет вид
в полярной системе координат имеет вид
Координаты многочлена 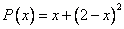 по базису
по базису 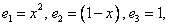 равны
равны
(4, -1, 3)
(1, 1, 1)
(1, 3, 1)
(-3, 4, 1)
На плоскости прямая х - у + 4 = 0
имеет угловой коэффициент k = 1
параллельна оси Оу
параллельна оси Ох
имеет угловой коэффициент k = -1
Вектор 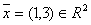 в базисе
в базисе 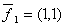 и
и 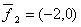 имеет координаты
имеет координаты
(1,1)
(1,3)
(3,1)
(3,3)
Уравнение прямой, проходящей через точку (-2,0) перпендикулярно прямой 3х+у+4 = 0, имеет вид
Модуль 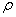 и аргумент
и аргумент 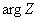 комплексного числа
комплексного числа 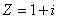 соответственно равны
соответственно равны
Координаты многочлена 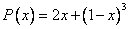 по базису
по базису 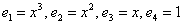 равны
равны
(-1, 3, -1, 1)
(2, 1, 1, 3)
(1, 2, 0, 0)
(1, -1, 3, -1)
Даны векторы 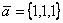 и
и 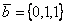 . Скалярное произведение векторов (
. Скалярное произведение векторов (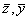 ), где
), где 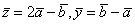 , равно
, равно
-2
2
1
0
Дано уравнение кривой второго порядка 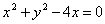 . Ее каноническое уравнение и тип кривой
. Ее каноническое уравнение и тип кривой
Квадратичная форма 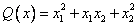 является
является
положительно определенной
неотрицательно определенной
отрицательно определенной
знаконеопределенной
Даны векторы 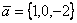 и
и 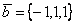 . Скалярное произведение векторов (
. Скалярное произведение векторов (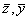 ), где
), где 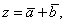
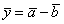 равно
равно
1
-3
2
0
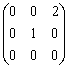
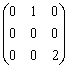
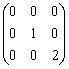
В пространстве многочленов степени 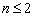 задан оператор дифференцирования
задан оператор дифференцирования 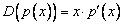 . Его матрица в базисе
. Его матрица в базисе 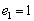 ,
, 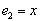 ,
, 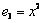 равна
равна
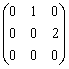
Длины векторов 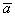 и
и 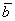 , соответственно, равны 1 и 4, их скалярное произведение равно 2. Угол между векторами
, соответственно, равны 1 и 4, их скалярное произведение равно 2. Угол между векторами 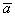 ,
, 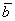 равен
равен
В системе уравнений 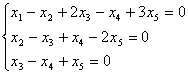 свободными переменными являются
свободными переменными являются
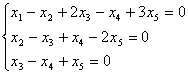 свободными переменными являются
свободными переменными являютсянет свободных переменных
Дано уравнение линии 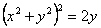 . В полярных координатах оно имеет вид
. В полярных координатах оно имеет вид
На плоскости прямую, проходящую через точку (2, 3) и имеющую угловой коэффициент k = 4, можно задать уравнением
у = 4х + 1
2х = 3у
3х - 2у = 0
у - 3 = 4(х - 2)
Дано уравнение гиперболы 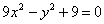 . Расстояние между вершинами гиперболы равно
. Расстояние между вершинами гиперболы равно
6
9
2
Данная поверхность 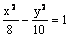 является
является
эллиптическим цилиндром
гиперболическим цилиндром
двухполостным гиперболоидом
однополостным гиперболоидом
К каноническому виду приведено следующее уравнение второго порядка
x2 + y2 + z2 + 2xy = 1
x = yz
3x2 + 4y2 = 12
yz = 1
Вектор 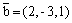
перпендикулярен плоскости 4x - 6y + 2z - 1 = 0
перпендикулярен прямой 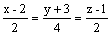
параллелен плоскости 4(x - 2) + (y +3) + (z + 1) = 0
параллелен прямой 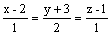
Объем треугольной пирамиды АВСD, где вершины А(1,1,1), В(-1,0,1), С(0,1,-1) и D(2,1,1), равен
3 куб.ед.
2 куб.ед.
0
Матрица перехода от стандартного базиса 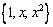 в пространстве многочленов к базису
в пространстве многочленов к базису 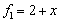 ,
, 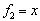 ,
, 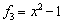 равна
равна

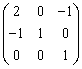
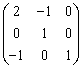
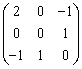
На плоскости ОХУ уравнения: а) 2х-3у+1 = 0; в) 2х-3у+3 = 0; с) 6х+4у-1 = 0; d) 3х+2у+5 = 0
являются уравнениями сторон квадрата
являются уравнениями сторон прямоугольника
являются уравнениями сторон ромба
являются уравнениями сторон трапеции
Даны уравнения кривых второго порядка: 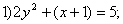

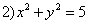
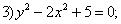
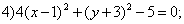 5)
5)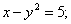
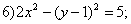
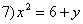 . Уравнениями парабол в этом списке являются уравнения
. Уравнениями парабол в этом списке являются уравнения
1, 3, 6
1, 4, 7
1, 5, 7
5, 6, 7
Парабола, симметричная относительно оси ОХ, с вершиной в начале координат проходит через точку М (-4, 2). Уравнение такой параболы имеет вид
Даны векторы 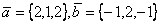 . Вектору
. Вектору 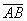 , где точки А (1,1,1) и В (2,-3,2), ортогональны векторы
, где точки А (1,1,1) и В (2,-3,2), ортогональны векторы
ни один из векторов
В пространстве многочленов степени 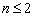 задан оператор дифференцирования
задан оператор дифференцирования 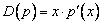 и функция
и функция 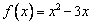 . Координаты образа
. Координаты образа 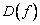 по базису
по базису 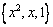 равны
равны
(0, -3, 2)
(-3, 2, 0)
(-3, 0, 2)
(2, -3, 0)
Матрица перехода от стандартного базиса в R3 к базису 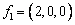 ,
, 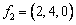 ,
, 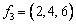 равна
равна
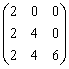
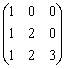
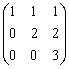
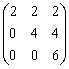
Координаты вершин треугольника АВС равны А (1,-1,0), В (0,1,1), С (1,2,0). Проекция 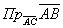 стороны
стороны 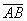 на сторону
на сторону 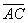 равна
равна
6
0
1
Максимальное число линейно независимых строк матрицы  равно
равно
 равно
равно2
4
3
1
На плоскости прямая х + у - 3 = 0
параллельна оси Ох
имеет угловой коэффициент k = 1
параллельна оси Оу
имеет угловой коэффициент k = -1
Среди множества решений систем уравнений 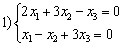 ,
, 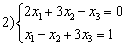 ,
, 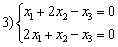 ,
, 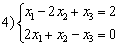 линейные подпространства образуют
линейные подпространства образуют
3, 4
1, 3
1, 2
2, 4
Даны две системы векторов 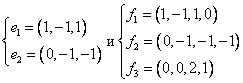 . Базис в R2 образуют системы
. Базис в R2 образуют системы
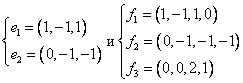 . Базис в R2 образуют системы
. Базис в R2 образуют системыникакая
обе
Два ненулевых вектора 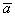 и
и 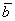 коллинеарны, если: 1)
коллинеарны, если: 1) 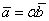 , где α- число; 2)
, где α- число; 2) 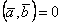 ; 3)
; 3) 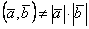 ; 4)
; 4) 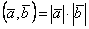 . Среди перечисленных утверждений верными являются
. Среди перечисленных утверждений верными являются
верных утверждений нет
1, 3
2, 3
1, 4
Базисом в пространстве 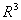 является система векторов
является система векторов
На плоскости ХОУ прямая 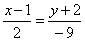
имеет направляющий вектор 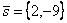
параллельна оси ОУ
параллельна оси ОХ
имеет нормальный вектор 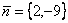
Через точки М1(3,0,3), М2(-1,0,0) и М3(2,2,0) проходит плоскость
х-2у-2z+2=0
6х-9у-8z+6=0
х-2у-z+1=0
х-у-2z+5=0
Все элементы матрицы 3-го порядка А увеличили в 3 раза, тогда определитель новой матрицы
увеличится в 9 раз
увеличится в 3 раза
увеличился в 27 раз
останется без изменения
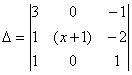 <0 верно при
<0 верно при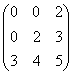 равен
равен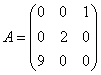 состоит из векторов
состоит из векторов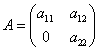 имеет вид
имеет вид