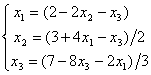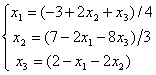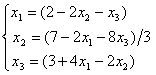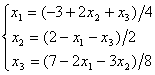Численные методы
Квадратурная формула Гаусса для n точек разбиения является точной для многочлена степени
2n
2n - 1
2n + 1
n
Выбор начального приближения на сходимость метода Зейделя при решении систем линейных уравнений
влияет всегда
влияет, если матрица не является верхней треугольной
влияет, если матрица не симметричная
не влияет
Задана линейная система уравнений с симметричной матрицей 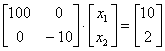 . Ее степень обусловленности равна
. Ее степень обусловленности равна
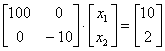 . Ее степень обусловленности равна
. Ее степень обусловленности равна5
−10
10
1000
Задана табличная функция y = f(x) 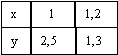 Интеграл
Интеграл 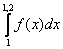 при вычислении методом трапеций равен
при вычислении методом трапеций равен
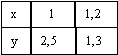 Интеграл
Интеграл 1
1,2
1,3
1,1
В таблично заданной функции производная в точке 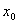 вычислена с использованием шагов h и 2h. Получены величины
вычислена с использованием шагов h и 2h. Получены величины 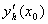 = 0,8 и
= 0,8 и 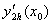 = 0,65. Погрешность формулы для вычисления производных имеет порядок
= 0,65. Погрешность формулы для вычисления производных имеет порядок 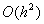 . Тогда уточненное значение производной
. Тогда уточненное значение производной 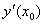 по методу Рунге равно
по методу Рунге равно
0,87
0,75
0,85
0,7
Подынтегральная функция y = f(x) задана таблично 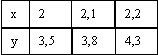 Вычисление интеграла
Вычисление интеграла 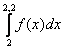 методом прямоугольников при h = 0,2 дает значение, равное
методом прямоугольников при h = 0,2 дает значение, равное
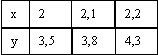 Вычисление интеграла
Вычисление интеграла 0,68
1,02
0,79
0,76
Единичная матрица - это диагональная матрица, у которой
на главной диагонали стоят только единицы
на главной диагонали стоят только нулевые элементы, а остальные элементы равны единице
все элементы матрицы равны единице
выше главной диагонали стоят только единицы
Порядком разностного уравнения называется
наибольший аргумент функции
количество конечных разностей, входящих в уравнение
количество дополнительных условий, определяющих единственность решения
наибольшая степень неизвестной функции
Формулы метода Эйлера с пересчетом для решения задачи Коши обыкновенного дифференциального уравнения имеют вид
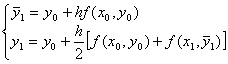
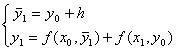
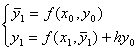
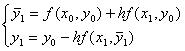
Для величин x и y заданы абсолютные погрешности D(x) = 0,01 и D(y) =1,5. Тогда абсолютная погрешность разности D(x−y) равна
−1,49
1,49
1,51
−1,51
Для величин x = 10 и y = 20 известны относительные погрешности δ(x) = 0,005 и δ(y) = 0,003. Относительная погрешность произведения δ( x ∙ y ) равна
0,000015
0,008
0,002
0,011
Для задачи Коши 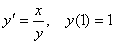 один шаг метода Эйлера с h = 0,2 дает результат для y(1,2), равный
один шаг метода Эйлера с h = 0,2 дает результат для y(1,2), равный
1,1
1,25
0,9
1,2
Для таблично заданной функции 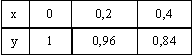 значение y(0,3), вычисленное с помощью квадратичной интерполяции, равно
значение y(0,3), вычисленное с помощью квадратичной интерполяции, равно
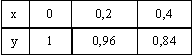 значение y(0,3), вычисленное с помощью квадратичной интерполяции, равно
значение y(0,3), вычисленное с помощью квадратичной интерполяции, равно0,94
0,9033
0,91
0,88
Разностными называются уравнения,
содержащие в записи знак минус
содержащие разности значений функции в соседних дискретных точках
связывающие неизвестные значения сеточной функции при нескольких значениях дискретного аргумента
полученные вычитанием двух линейных уравнений
Отделить корни при решении нелинейного уравнения F( x ) = 0 - это значит
для каждого корня указать интервал, в котором он будет единственным
отделить положительные корни от отрицательных
расставить корни в порядке их возрастания
для каждого корня указать область притяжения
Для решения нелинейного уравнения второй порядок сходимости имеют
секущих
Ньютона
половинного деления
итераций
В таблично заданной функции производная в точке 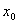 вычислена с использованием шагов h и 2h. Получены величины
вычислена с использованием шагов h и 2h. Получены величины 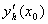 = 1,5 и
= 1,5 и 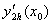 = 1,3. Погрешность формулы для вычисления производных имеет порядок
= 1,3. Погрешность формулы для вычисления производных имеет порядок 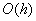 . Тогда уточненное значение производной
. Тогда уточненное значение производной 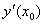 по методу Рунге равно
по методу Рунге равно
1,4
1,7
1,6
1,65
Заданы нелинейные системы 1)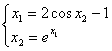 2)
2) 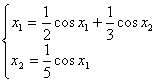 3)
3) 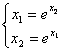 Сходимость метода простой итерации гарантирована для систем
Сходимость метода простой итерации гарантирована для систем
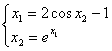 2)
2) 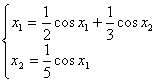 3)
3) 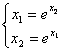 Сходимость метода простой итерации гарантирована для систем
Сходимость метода простой итерации гарантирована для системвторой
первой
второй и третьей
первой и второй
Если на отрезке [ a , b ] функция F( x ) непрерывна, F( a ) ∙ F( b ) < 0 , то метод половинного деления для уравнения F( x ) = 0 сходится
при 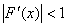
всегда
при F′( x ) > 0
если F( x ) ∙ F′( x ) > 0
Для ускорения сходимости метода итераций способом Стеффенсена необходимо иметь
три начальных приближения x0 , x1 , x2
одно начальное приближение x0
четыре начальных приближения x0 , x1 , x2 , x3
два начальных приближения x0 , x1
Критерий близости двух функций f(x) и φ(x) при среднеквадратичном приближении заключается в том, что на заданной системе точек 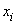 ( i = 0, 1, 2, n ) минимизируется выражение
( i = 0, 1, 2, n ) минимизируется выражение
Результат вычисления интеграла 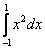 методом трапеций с разбиением на два интервала (h = 1) равен
методом трапеций с разбиением на два интервала (h = 1) равен
0,5
0,25
1
0,333333
Для величин x = 2 и y = 5 известны относительные погрешности δ(x) = 0,005 и δ(y) = 0,002. Относительная погрешность частного δ( x ∕ y ) равна
0,003
0,0025
0,007
0,00001
Погрешность метода трапеций на всем отрезке интегрирования имеет порядок k, равный
1,5
2
3
1
Задано дифференциальное уравнение 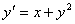 и начальное условие y(0)=1. Один шаг метода Эйлера при h = 0,2 дает значение
и начальное условие y(0)=1. Один шаг метода Эйлера при h = 0,2 дает значение
1,5
1,1
1,2
1,25
Дана система линейных уравнений 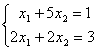 . Для сходящегося метода Зейделя ее надо записать в виде
. Для сходящегося метода Зейделя ее надо записать в виде
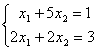 . Для сходящегося метода Зейделя ее надо записать в виде
. Для сходящегося метода Зейделя ее надо записать в виде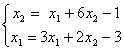
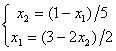
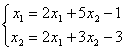
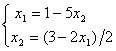
Задана линейная система уравнений в матричном виде 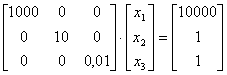 . Ее степень обусловленности равна
. Ее степень обусловленности равна
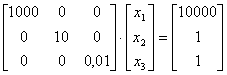 . Ее степень обусловленности равна
. Ее степень обусловленности равна104
0,01
10
105
Дано уравнение x3 - x = 0 и начальное приближение x0 = 1. Результат одного шага метода Ньютона равен
x1 = 1
x1 = 2
x1 = −1
x1 = 0,5
Разностное уравнение 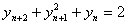 является
является
нелинейным
линейным
линейным уравнением с постоянными коэффициентами
квазилинейным
Заданы системы линейных уравнений 1)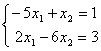 2)
2) 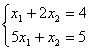 3)
3) 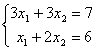 . Свойством диагонального преобладания обладают матрицы систем
. Свойством диагонального преобладания обладают матрицы систем
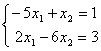 2)
2) 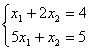 3)
3) 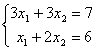 . Свойством диагонального преобладания обладают матрицы систем
. Свойством диагонального преобладания обладают матрицы систем1 и 3
3
2
2 и 3
Для системы линейных уравнений 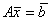 известны обратная матрица A-1 и вектор правых частей
известны обратная матрица A-1 и вектор правых частей 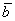 A-1 =
A-1 = 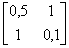
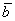 =
= 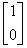 . Тогда вектор решения системы
. Тогда вектор решения системы 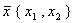 равен
равен
{ 0,5 ; 1 }
{ 1 ; 0,1 }
{ 1,5 ; 1,1 }
{ 1 ; 0,5 }
Сходимость итерационного метода решения систем линейных уравнений зависит от
количества нулей в матрице
начального приближения системы
величины правых частей системы
вида матрицы системы
Приближенные значения интеграла с шагами h и h ∕ 2 равны 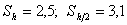 . Погрешность метода имеет вид
. Погрешность метода имеет вид 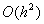 . Уточненное значение интеграла по методу Рунге равно
. Уточненное значение интеграла по методу Рунге равно
2,9
3,15
3,5
3,3
Дана система 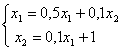 задано начальное приближение ( 1; 1 ). Один шаг метода Зейделя дает первое приближение
задано начальное приближение ( 1; 1 ). Один шаг метода Зейделя дает первое приближение
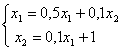 задано начальное приближение ( 1; 1 ). Один шаг метода Зейделя дает первое приближение
задано начальное приближение ( 1; 1 ). Один шаг метода Зейделя дает первое приближение( 0,6 ; 1,06 )
( 0,6 ; 1,1 )
( 0,6 ; 1 )
( 0,1 ; 1,06 )
Для таблично заданной функции 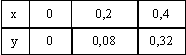 значение y(0,1), вычисленное с помощью квадратичной интерполяции, равно
значение y(0,1), вычисленное с помощью квадратичной интерполяции, равно
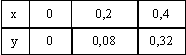 значение y(0,1), вычисленное с помощью квадратичной интерполяции, равно
значение y(0,1), вычисленное с помощью квадратичной интерполяции, равно0,02
0,03
0,04
0,028
Параметр релаксации ω для метода верхней релаксации при решении системы линейных уравнений лежит в пределах
2 < ω < 3
0 < ω < 1
1 < ω < 2
−1 < ω < 0
Метод половинного деления для уравнения F( x ) = 0 для непрерывной функции F( x ), удовлетворяющей на отрезке [ a , b ] условию F(a ) ∙ F(b) < 0 сходится
при 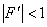
всегда
при 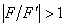
при 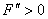
LU-разложение матрицы А представляет ее в виде
произведения симметричной матрицы на диагональную матрицу
произведение верхней треугольной матрицы на диагональную матрицу
произведения нижней треугольной матрицы на верхнюю треугольную матрицу
суммы двух треугольных матриц
Для линейной системы уравнений вычисления по итерационной формуле 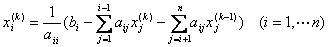 называют методом
называют методом
Ньютона
Гаусса
Зейделя
простой итерации
Для нелинейного уравнения F( x ) = 0 задан интервал [ a, b ] , на котором F( a )∙F( b ) < 0 и F( x ) непрерывна. На нем можно гарантировать сходимость
метода Ньютона
методов половинного деления и секущих
методов половинного деления и хорд
методов Ньютона и секущих
Даны системы уравнений 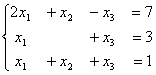
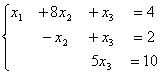
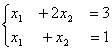 Для обратного хода метода Гаусса подготовлены следующие
Для обратного хода метода Гаусса подготовлены следующие
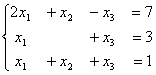
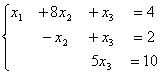
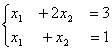 Для обратного хода метода Гаусса подготовлены следующие
Для обратного хода метода Гаусса подготовлены следующие1 и 2
только 2
ни одна из них
только 3
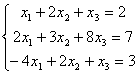 Для сходимости итерационного метода ее надо записать в виде
Для сходимости итерационного метода ее надо записать в виде