Математика (курс 9)
Решением уравнения Uxx + Uy = 0 является функция
U = excosy
U = e-xsiny
U = eycosx
U = e-ysinx
Уравнения характеристик для дифференциального уравнения 4ut - 3ux = 0 имеют вид
Функция U является решением уравнения Utt = Uxx + sinx × cost. Тогда решением этого же уравнения будет функция
U + (х - t)2
U + x2 - t2
U + x2t2
U + t2 - x2
Функция U является решением уравнения Uxx + Uyy = sinx + siny. Тогда решением этого же уравнения будет функция
U + x2 + y2
U + sinx + siny
U + (х - y)2
U + x2 - y2
Уравнения характеристик для дифференциального уравнения ut + 4ux = 0 имеют вид
Область, в которой уравнение 2Uxx + yUхy - xUyy = 0 имеет гиперболический тип, расположена
вне параболы у2 = - 8х
вне параболы у2 = 8х
внутри параболы у2 = 8х
внутри параболы у2 = - 8х
Даны два утверждения: 1) уравнение Uxх + уUy + U = 0 имеет второй порядок, 2) уравнение Uх + уUу + 4U = 0 линейное однородное первого порядка. Утверждения
оба неверны
первое верно, второе неверно
первое неверно, второе верно
оба верны
Функция U является решением уравнения Utt = Uxx - cosx×e-t. Тогда решением соответствующего однородного уравнения будет функция
U - cosx×e-t
U + cosx×e-t
U - 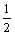 cosx×e-t
cosx×e-t
U + 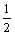 cosx×e-t
cosx×e-t
Функция у = sin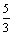 x является решением краевой задачи
x является решением краевой задачи
y¢¢ + 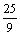 y = 0, y¢(0) = y(3p) = 0
y = 0, y¢(0) = y(3p) = 0
y¢¢ + 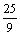 y = 0, y(0) = y(3p) = 0
y = 0, y(0) = y(3p) = 0
y¢¢ + 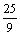 y = 0, y¢(0) = y(3) = 0
y = 0, y¢(0) = y(3) = 0
y¢¢ + 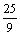 y = 0, y(0) = y(3) = 0
y = 0, y(0) = y(3) = 0
Коэффициент В(l) в задаче Коши для уравнения теплопроводности Ut = Uxx, U(x,0) = j(x) вычисляется по формуле В(l) = 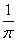
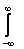 j(x)sinx
j(x)sinx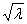 dx Тогда коэффициент B(l) при U(x,0) = j(x) =
dx Тогда коэффициент B(l) при U(x,0) = j(x) = 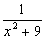 равен
равен
1
0
Волновое уравнение на плоскости имеет вид
Utt + a2Uxx = 0
Utt + Uxx = Uy
Ut = a2(Uxx + Uyy)
Utt = a2(Uxx + Uyy)
Методом Даламбера решается задача Коши для уравнения
волнового
Лапласа
теплопроводности
Пуассона
Решением уравнения xUx + Uy - xU = 0 является функция
U = yex + y
U = yex - y
U = xex + y
U = xex - y
Функция u(x,t) =(x-at)2 является решением уравнения
ut - aux = 0
utt + a2uxx = 0
ut + aux = 0
ut = a2uxx
Решение уравнения колебания струны Utt = a2Uxx с начальным отклонением U(x,0) = j(x) и начальной скоростью Ut(x,0) = y(x) записывается в виде U(x,t) = 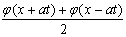 +
+ 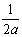
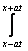 y(x)dx Тогда решение уравнения Utt = 4Uxx при начальном отклонении U(x,0) = х2 и начальной скоростью Ut (x,0) = 0 имеет вид
y(x)dx Тогда решение уравнения Utt = 4Uxx при начальном отклонении U(x,0) = х2 и начальной скоростью Ut (x,0) = 0 имеет вид
U(x,t) = 2x2 + t2
U(x,t) = x2 + 2t2
U(x,t) = x2 + 4t2
U(x,t) = x2 - 4t2
Параболический тип имеет уравнение
2Uxx + Uxy = 0
3Uxx - Uyy = 0
Uxx + 2Uxy - Uyy = 0
4Uxx - 8Uxy + 4Uyy = 0
Область, в которой уравнение 2Uxx - yUxy - xUyy = 0 имеет эллиптический тип, находится
вне параболы 8у = - х2
внутри параболы 8у = - х2
вне параболы у2 = -8х
внутри параболы у2 = -8х
Функция у = cos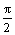 x является решением краевой задачи
x является решением краевой задачи
y¢¢ + 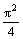 y = 0, y¢(0) = y¢(2) = 0
y = 0, y¢(0) = y¢(2) = 0
y¢¢ + p2y = 0, y¢(0) = y(2) = 0
y¢¢ + p2y = 0, y¢(0) = y¢(2) = 0
y¢¢ + 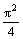 y = 0, y¢(0) = y(2) = 0
y = 0, y¢(0) = y(2) = 0
Функция f(x) = x разлагается в ряд Фурье 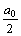 +
+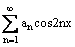 на отрезке [0,
на отрезке [0, 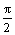 ]. Коэффициент a0 равен
]. Коэффициент a0 равен
p
0
Преобразованием Фурье функции f(x) называется функция вида
F(s) =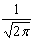
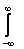 f(x)cos(sx)dx
f(x)cos(sx)dx
F(s) =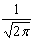
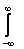 f(x)sinsdx
f(x)sinsdx
F(s) =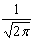
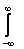 f(x)e-xsdx
f(x)e-xsdx
F(s) =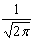
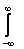 f(x)e-ixsdx
f(x)e-ixsdx
Область, в которой уравнение (1 - x2)Uxx + yUxy + Uyy = 0 имеет эллиптический тип, находится
вне эллипса 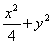 = 1
= 1
внутри эллипса 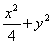 = 1
= 1
внутри эллипса х2 + 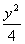 = 1
= 1
вне эллипса х2 + 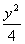 = 1
= 1
Xарактеристики уравнения ut + 4ux = 0 имеют вид
t = 4s + C1, x = 4s + C2
t = s + C1, x = 4s + C2
t = s + C1, x = -4s + C2
t = s + C1, x = 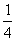 s + C2
s + C2
Решение уравнения колебания струны Utt = a2Uxx с начальным отклонением U(x,0) = j(x) и начальной скоростью Ut(x,0) = y(x) записывается в виде U(x,t) = 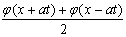 +
+ 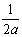
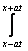 y(x)dx Тогда решение уравнения Utt = а2Uxx при начальном отклонении U(x,0) =
y(x)dx Тогда решение уравнения Utt = а2Uxx при начальном отклонении U(x,0) = 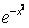 и начальной скоростью Ut (x,0) = 0 имеет вид
и начальной скоростью Ut (x,0) = 0 имеет вид
U(x,t) = 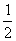 (
(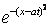 +
+ 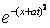 )
)
U(x,t) = 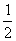 (
(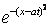 +
+ 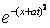 )
)
U(x,t) = 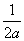 (
(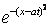 +
+ 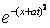 )
)
U(x,t) = 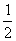 (
(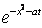 +
+ 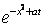 )
)
Решение задачи y¢¢ +9p2у = 0, у (0) = у¢(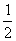 ) = 0 имеет вид
) = 0 имеет вид
y = cos3х
y = cos3pх
y = sin3х
y = sin3pх
Решение задачи y¢¢ +16у = 0, у¢(0) = у¢(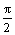 ) = 0 имеет вид
) = 0 имеет вид
y = cos4х
y = sin4pх
y = cos4pх
y = sin4х
Даны два утверждения: 1) уравнение y(Ux)2 + (Uy)2 - z(Uz)2 = 0 имеет второй порядок, 2) уравнение у3(Uxy) + х3(Uyz) - z3(Uzz) = 0 имеет первый порядок. Утверждения
первое неверно, второе верно
оба верны
оба неверны
первое верно, второе неверно
Решение уравнения колебания струны Utt = a2Uxx с начальным отклонением U(x,0) = j(x) и начальной скоростью Ut(x,0) = y(x) записывается в виде U(x,t) = 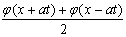 +
+ 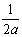
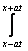 y(x)dx Тогда решение уравнения Utt = а2Uxx при начальном отклонении U(x,0) = 0 и начальной скоростью Ut (x,0) = х имеет вид
y(x)dx Тогда решение уравнения Utt = а2Uxx при начальном отклонении U(x,0) = 0 и начальной скоростью Ut (x,0) = х имеет вид
U(x,t) = xt
U(x,t) = x2t2
U(x,t) = xt2
U(x,t) = xt3
Даны два утверждения: 1) уравнение (Uz)2 - (Uy)2 + U2 = 0 нелинейное, 2) уравнение Uxx + Uуy + Uzz = U однородное. Утверждения
оба неверны
первое неверно, второе верно
первое верно, второе неверно
оба верны
Матрицей системы уравнений 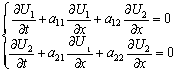 называется матрица
называется матрица 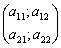 . Тогда матрица системы уравнений
. Тогда матрица системы уравнений 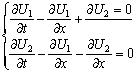 равна
равна
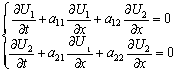 называется матрица
называется матрица 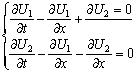 равна
равнаФункция U является решением уравнения Utt = Uxx + sinx + cost. Тогда решением этого же уравнения будет функция
U - x2 + t2
U - x2t2
U + x2 + t2
U + x2 - t2
Решением уравнения Uxx - Uy = 0 является функция
U = e-ysinx
U = e-xsiny
U = eycosx
U = excosy
Функции U1 = 3xy + 4 и U2 = 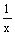 - 2 являются решениями уравнения
- 2 являются решениями уравнения
Ux + Uy = 0
Uxx - Uyy = 0
Uxx + Uyy = 0
Даны два утверждения: 1) уравнение у3Uху + x3Uуz - z3Uzz = U линейное неоднородное, 2) уравнение (Uzz)2 - x2(Uу)2 + y2(Ux)2 = 0 имеет второй порядок. Утверждения
оба верны
первое неверно, второе верно
первое верно, второе неверно
оба неверны
Общее решение уравнения aUt + bUx = 0 записывается в виде U(x,t) = C(ax-bt), где С(u) - произвольная дифференцируемая по u функция. Тогда общее решение уравнения 4Ut + Ux = 0 записывается в виде
U(x,t) = C1(x+4t) + C2(x-4t)
U(x,t) = C(x + 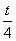 )
)
U(x,t) = C(x+4t)
U(x,t) = C(x - 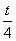 )
)
Даны два утверждения: 1) уравнение xUху - xyUz + xyz = 0 линейное неоднородное, 2) уравнение x2Ux - y2Uу + U2 = 0 линейное однородное. Утверждения
оба неверны
оба верны
первое верно, второе неверно
первое неверно, второе верно
Решение задачи y¢¢ +p2у = 0, у(0) = у¢(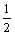 ) = 0 имеет вид
) = 0 имеет вид
y = sinх
y = sinpх
y = cosх
y = cospх
Преобразование Фурье F[f] по t функции f(x,t) имеет свойство
F[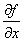 ] =
] = 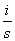 F[f]
F[f]
F[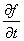 ] =
] = 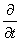 F[f]
F[f]
F[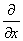 ] =
] = 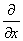 F[f]
F[f]
F[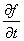 ] =
] = 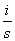 F[f]
F[f]
Функция у = cos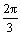 x является решением краевой задачи
x является решением краевой задачи
y¢¢ + 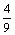 y = 0, y¢(0) = y¢(p) = 0
y = 0, y¢(0) = y¢(p) = 0
y¢¢ + 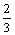 y = 0, y¢(0) = y¢(p) = 0
y = 0, y¢(0) = y¢(p) = 0
y¢¢ + 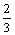 y = 0, y¢(0) = y¢(3p) = 0
y = 0, y¢(0) = y¢(3p) = 0
Решение уравнения колебания струны Utt = a2Uxx с начальным отклонением U(x,0) = j(x) и начальной скоростью Ut(x,0) = y(x) записывается в виде U(x,t) = 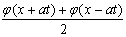 +
+ 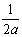
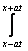 y(x)dx Тогда решение уравнения Utt = а2Uxx при начальном отклонении U(x,0) = sinx и начальной скоростью Ut (x,0) = 0 имеет вид
y(x)dx Тогда решение уравнения Utt = а2Uxx при начальном отклонении U(x,0) = sinx и начальной скоростью Ut (x,0) = 0 имеет вид
U(x,t) = 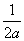 (sin(x-at) + sin(x+at))
(sin(x-at) + sin(x+at))
U(x,t) = 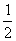 (sin(x-at) + sin(x+at))
(sin(x-at) + sin(x+at))
U(x,t) = 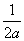 (cos(x-at) + cos(x+at))
(cos(x-at) + cos(x+at))
U(x,t) = 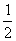 (cos(x-at) + cos(x+at))
(cos(x-at) + cos(x+at))
Косинус-преобразование Фурье функции f(x) записывается в виде: Fc(a) = 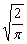
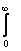 f(x)cosax dx. Найти косинус-преобразование Фурье функции
f(x)cosax dx. Найти косинус-преобразование Фурье функции 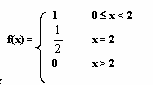
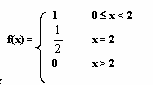
Порядком дифференциального уравнения называется
наивысшая степень производных, входящих в уравнение
наивысшая степень функций, входящих в уравнение
наивысшая степень переменных, входящих в уравнение
наивысший порядок производных, входящих в уравнение
Функции U1 = ln (x - y) и U2 = ex + y являются решениями уравнения
Uy - Uxx = 0
Ux - Uyy = 0
Uxx + Uyy = 0
Uxx - Uyy = 0
Эллиптический тип имеет уравнение
3Uxy + 4Uyy = 0
Uxx + 2Uxy + 3Uyy = 0
3Uxx - 2Uxy - Uyy = 0
4Uxx - 4Uxy + Uyy = 0
Функция U является решением уравнения Ut = Uxx - etcosx. Тогда решением соответствующего однородного уравнения будет функция
U - 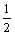 etsinx
etsinx
U + 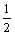 etsinx
etsinx
U - 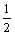 etcosx
etcosx
U + 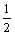 etcosx
etcosx
Решение задачи y¢¢ +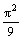 у = 0, у (0) = y¢(
у = 0, у (0) = y¢(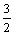 ) = 0 имеет вид
) = 0 имеет вид
y = cos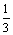 x
x
y = cos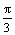 x
x
y = sin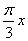
y = sin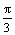 x
x
Собственными значениями матрицы системы уравнений 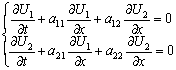 называются корни уравнения второго порядка
называются корни уравнения второго порядка 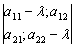 = 0 Тогда собственными значениями матрицы системы уравнений
= 0 Тогда собственными значениями матрицы системы уравнений 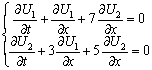 являются значения
являются значения
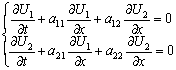 называются корни уравнения второго порядка
называются корни уравнения второго порядка 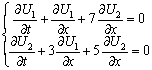 являются значения
являются значенияl1 = -2 ; l2 = 8
l1 = -1 ; l2 = 1
l1 = -1 ; l2 = 3
l1 = 3 ; l2 = -5
Уравнение (x + у)2Uxx + 2(xy + у2)Uxy +y2Uyy = 0 имеет параболический тип
при всех х > -у > 0
при всех (х + у) > 0
при всех (х, у), кроме (0, 0)
при всех (х, у)
Решение задачи y¢¢ +p2у = 0, у¢(0) = у(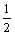 ) = 0 имеет вид
) = 0 имеет вид
y = cospх
y = cosx
y = cos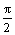 x
x
y = sinpх
Функции U1 = 2xy + 5x - 3y и U2 = 5(x2 - y2) являются решениями уравнения
Uxx + Uyy = 0
Uxx - Uyy = 0
Uyy + U = 0
Ux + Uyy = 0