Теория вероятностей, математическая статистика и случайные процессы
Вероятность события А равна Р(1. = 0,3; вероятность В равна Р(2. = 0,2. Известно, что события А и В независимы. Тогда вероятность произведения P(AB) равна
0,06
0,5
0,32
0,23
Выберите верные утверждения
= 30
= 20
= 15
= 10Даны два множества А = {1, 2, 4, 6, 8, 10} и B = {1, 4, 8, 12}. Укажите соответствие между операциями и множествами
A\B
{1, 4, 8}
AÈB
{1, 2, 4, 6, 8, 10, 12}
AÇB
{2, 6, 10}
Случайная величина Х имеет распределение Пуассона с параметром l = 4. Ее числовые характеристики равны
MX = 4; DX = 16 σX = 4
MX = 4; DX = 4 σX = 2
MX = 2; DX = 2 σX =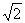 
MX = 2; DX = 4 σX = 2
Игральный кубик бросают один раз. Вероятность того, что на верхней грани выпадет четное число очков, равна
1/3
0
1/2
2/3
Вероятность появления события А в 40 независимых испытаниях, проводимых по схеме Бернулли, равна 0,7. Тогда дисперсия числа появлений этого события равна
28
8,4
1,75
0,84
Петя сдаст экзамен на отлично с вероятностью 0,9; а Вася – с вероятностью 0,1. Вероятность того, что оба они сдадут экзамен на «отлично», равна
0,9
1
0,91
0,09
Вероятность появления события А в 20 независимых испытаниях, проводимых по схеме Бернулли, равна 0,1. Тогда дисперсия числа появлений этого события равна
0,18
0,05
2
1,8
В урне 10 шаров: 5 красных, 3 белых, 2 чёрных. Студент берёт наугад шар. Рк – вероятность вынуть красный шар, Рб – вероятность вынуть белый шар, Рч – вероятность вынуть чёрный шар
Рб
0,5
Рч
0,2
Рк
0,3
Вероятность наступления некоторого события не может быть равна
0,5
1
0,2
2
Пусть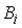 
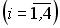- события, заключающиеся в том, что произошел обрыв в цепи сопротивлений 
, 
, 
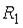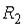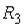или 
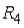
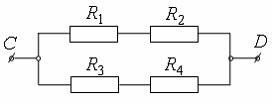Событие 
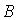- за время 
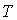произошел обрыв в электрической цепи между точкам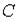и 
и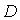 
. Тогда 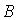представимо через 
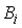следующим образом …
- события, заключающиеся в том, что произошел обрыв в цепи сопротивлений , , или Событие - за время произошел обрыв в электрической цепи между точками и . Тогда представимо через следующим образом …
По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию, равны 0,3 и 0,05. Тогда вероятность банкротства обоих предприятий равна
0,015
0,665
0,15
0,35
Два одноклассника поступают в институт на разные факультеты. Первый одноклассника поступит с вероятностью 0,5; второй – с вероятностью 0,6. Вероятность того, что оба одноклассника поступят, равна
1,1
0,03
0,7
0,3
В квадрат со стороной 9 брошена точка. 
Тогда вероятность того, что она попадет в выделенную область, равна …
Тогда вероятность того, что она попадет в выделенную область, равна …
MX = 5, MY = 2. Используя свойства математического ожидания, найдите M(2X - 3Y). Ответ дайте числом
Послано 6 радиосигналов. Вероятность приёма каждого из них равна 0,9. Вероятность того, что будет принято 5 сигналов, равна
(0,9)5(0,1)(0,9)5
(0,9)5×0,1
(0,9)5(0,1)Среднеквадратическое отклонение непрерывной случайной величины вычисляется по формуле
σ(X) =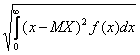 
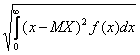
σ(X) =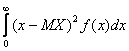 
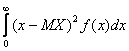
σ(X) =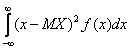 
σ(X) =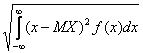 
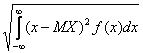
В первой урне 3 белых и 7 черных шаров. Во второй урне 5 белых и 5 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна…
0,8
0,4
0,1
0,45
В урне находятся 3 белых и 2 черных шара. Из урны поочередно вынимают два шара. Тогда вероятность того, что оба шара белые равна …
В первой урне 3 белых и 7 черных шаров. Во второй урне 6 белых и 4 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна…
0,15
0,9
0,5
0,45
В урне из 8 шаров имеется 3 красных. Наудачу берут два шара. Тогда вероятность того, что среди них ровно один красный шар, равна …
По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию, равны 0,3 и 0,35. Тогда вероятность банкротства обоих предприятий равна
0,465
0,095
0,105
0,65
Момент случайной величины Х порядка “n” определяется выражением
– M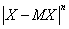
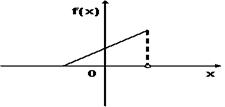
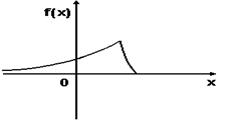
График плотности вероятностей для нормального распределения изображен на рисунке
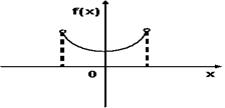
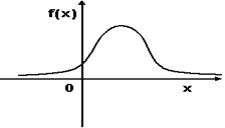
Вероятность стрелку попасть в мишень равна 0,9. Стрелок стреляет три раза. Р1 – вероятность попасть один раз. Р2 – вероятность попасть два раза. Р3 – вероятность попасть три раза
Р2
0,729
Р1
0,027
Р3
0,243
В тире лежат два ружья. Вероятность стрелку попасть из первого ружья 0,9. Вероятность стрелку попасть из второго ружья 0,6. Стрелок заходит в тир, первое ружьё берёт с вероятностью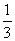 
, второе ружьё берёт с вероятностью 
, два раза стреляет. Р0 – вероятность, что попаданий нет. Р1 – вероятность, что попал один раз. Р2 – вероятность двух попаданий
, второе ружьё берёт с вероятностью 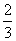, два раза стреляет. Р0 – вероятность, что попаданий нет. Р1 – вероятность, что попал один раз. Р2 – вероятность двух попаданийР2
0,11
Р1
0,38
Р0
0,51
Первый стрелок попадает в мишень с вероятностью 0,9; а второй – с вероятностью 0,5. Каждый стрелок делает по одному выстрелу. Вероятность того, что оба они попадут в мишень, равна
0,45
1,4
0,55
1
По выборке объема n=100 построена гистограмма частот: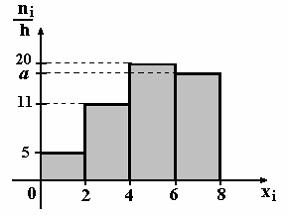 
Тогда значение а равно
Тогда значение а равно15
64
14
13
Фирма планирует выпуск двух новых изделий. По оценкам эксперта, хороший спрос на первое изделие будет с вероятностью 0,9; на второе – с вероятностью 0,8. Вероятность хорошего спроса на оба изделия равна
1,7
0,8
0,072
0,72
Игральный кубик бросают один раз. Вероятность того, что на верхней грани выпадет число очков, меньшее чем пять, равна
1/3
2/3
0
5/6
На некоторой фабрике машина А производит 40% продукции, а машина B - 60%. В среднем 9 из 1000 единиц продукции, произведенных машиной А, и 1 из 250, произведенных машиной B, оказываются бракованными. Какова вероятность, что случайно выбранная единица продукции окажется бракованной? Ответ дайте десятичной дробью
Стрелок попадает в цель с вероятностью 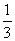. Стрелок стреляет три раза. Р3 – вероятность попасть три раза. Р2 – вероятность попасть два раза, один раз смазать. Р1 – вероятность попасть один раз, два раза смазать. Р0 – вероятность все три раза смазать. Выберите верные утверждения
. Стрелок стреляет три раза. Р3 – вероятность попасть три раза. Р2 – вероятность попасть два раза, один раз смазать. Р1 – вероятность попасть один раз, два раза смазать. Р0 – вероятность все три раза смазать. Выберите верные утвержденияР2 =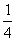 
Р0 =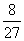 
Р3 =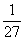 
Р1 =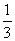
Вероятность появления события А в 40 независимых испытаниях, проводимых по схеме Бернулли, равна 0,8. Тогда дисперсия числа появлений этого события равна
6,4
0,64
0,02
32
Петя сдаст экзамен на отлично с вероятностью 0,9; а Вася – с вероятностью 0,1. Вероятность того, что оба они сдадут экзамен на «отлично», равна
0,9
0,09
1
0,91
Вероятность появления события А в 20 независимых испытаниях, проводимых по схеме Бернулли, равна 0,4. Тогда дисперсия числа появлений этого события равна
4,8
0,48
8
0,02
Дан закон распределения вероятностей дискретной случайной величины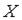 
: 
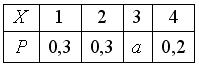Тогда значение 
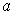равно…
: Тогда значение равно…0,2
– 0,8
0,1
0,8
С первого станка на сборку поступает 60%, со второго – 40% всех деталей. Среди деталей первого станка 80% стандартных, второго – 90%. Взятая наудачу деталь оказалась стандартной. Тогда вероятность того, что она изготовлена на втором станке, равна …
Случайная величина Х распределена показательно с параметром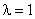 
, тогда P(X > 0) равна
, тогда P(X > 0) равна0
0,25
1
0,5
Случайная величина распределена показательно с параметром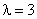 
, тогда P(X > - 3) равна
, тогда P(X > - 3) равна0,5
1
0,4
0
Работают 8 ламп. Вероятность перегорания лампы в течение некоторого времени равна 0,02. Вероятность того, что за это время перегорит только одна из восьми ламп, равна
×(0,02)(0,02)×(0,98)7
×(0,02)×(0,98)7(0,98)7
В урне 4 билета. Из них 2 выигрышных. Вынимаем три билета случайным образом. Р3 – вероятность вынуть три выигрышных билета. Р2 – вероятность вынуть два выигрышных билета. Р1 – вероятность вынуть один выигрышный билет. Р0 – вероятность, что все билеты не выиграли. Выберите верные утверждения
Р3 = 0,1
Р1 = 0,5
Р2 = 0,4
Р0 = 0
Математическое ожидание непрерывной случайной величины MX - это
MX = 
MX =
MX =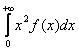 
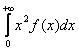
MX =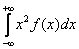
Пусть X – дискретная случайная величина, заданная законом распределения вероятностей: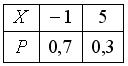 
Тогда математическое ожидание этой случайной величины равно…
Тогда математическое ожидание этой случайной величины равно…2
0,8
2,2
1,5
Два события А и В называются независимыми, если
Р(А×2. = Р(1. + Р(2.
Р(А×2. =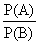 
Р(А×2. = Р(1. ×Р(2.
Р(А×2. = Р(1. - Р(2.
Дан закон распределения вероятностей дискретной случайной величины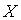 
: 
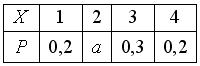Тогда значение 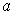равно…
: Тогда значение равно…0,3
0,7
0,2
– 0,7
По выборке объема n=100 построена гистограмма частот: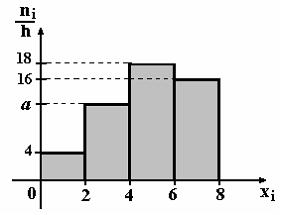 
Тогда значение а равно
Тогда значение а равно12
11
62
13
Петя сдаст экзамен на отлично с вероятностью 0,9; а Вася – с вероятностью 0,1. Вероятность того, что оба они сдадут экзамен на «отлично», равна
0,91
0,9
1
0,09
Дискретная случайная величина Х имеет закон распределения вероятностей
4,4
2,6
7
1
По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию, равны 0,1 и 0,25. Тогда вероятность банкротства обоих предприятий равна…
0,25
0,35
0,675
0,025
Два стрелка стреляют по мишени. Вероятность попадания в цель у одного стрелка 0,6, у другого – 0,7. Найти вероятность того, что цель будет по ражена обоими стрелками. Ответ дайте десятичной дробью