Теория вероятностей, математическая статистика и случайные процессы
Дискретная случайная величина Х задана законом распределения вероятностей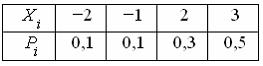 
Тогда значение интегральной функции распределения вероятностей 
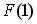равно …
Тогда значение интегральной функции распределения вероятностей равно …0,9
0,2
0,6
0,8
F(x) - функция распределения. F(+ ¥) равна
F(+¥) = 0,5
F(+¥) = 0
F(+¥) = -1
F(+¥) = 1
Вероятность стрелку попасть в мишень равна 0,6. Стрелок стреляет два раза. Р0 – вероятность, что попаданий нет. Р1 – вероятность, что попал один раз Р2 – вероятность двух попаданий.
Р2
0,16
Р1
0,48
Р0
0,36
Возводятся два жилых дома. Вероятность сдачи в срок одного из них 0,8, а другого – 0,9. Тогда вероятность сдачи в срок хотя бы одного дома равна
0,8 + 0,9
0,6
0,8×0,9
0,8 + 0,9 – 0,72
Автоматическая телефонная станция получает в среднем 3 вызова в минуту. Вероятность того, что станция получит точно 6 вызовов за данную минуту, равна
e-60,5
0,4
e-3По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию, равны 0,5 и 0,35. Тогда вероятность банкротства обоих предприятий равна
0,185
0,175
0,85
0,325
В урне 5 билетов. Из них 2 выигрышных. Вынимаем три билета случайным образом. Р3 – вероятность вынуть три выигрышных билета. Р2 – вероятность вынуть два выигрышных билета. Р1 – вероятность вынуть один выигрышный билет. Р0 – вероятность, что все билеты не выиграли. Выберите верные утверждения
Р3 = 0,1
Р2 = 0,2
Р1 = 0,6
Р0 = 0,1
Вероятность билету быть выигрышным равна 0,2. Вероятность того, что среди пяти купленных наудачу билетов хотя бы один выигрышный, равна
1 – (0,8)5
0,2
(0,2)5
(0,8)5
Два события будут несовместными, если
Р(А2. = 1
Р(А2. = 0
Р(А2. = Р(1.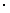 
Р(2.
Р(2.Р(А2. = Р(1. + Р(2.
Среднеквадратическое отклонение дискретной случайной величины вычисляется по формуле
σ(X) =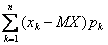 
σ(X) =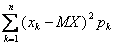 
σ(X) =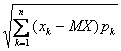 
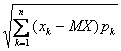
σ(X) =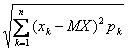 
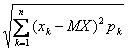
В урне находится 5 белых и 5 черных шаров. Из урны вынимаются четыре шара. Вероятность того, что два шара будут белыми, а два черными, равна …
Вероятность стрелку попасть в мишень равна 0,7. Стрелок стреляет два раза. Р0 – вероятность, что попаданий нет. Р1 – вероятность, что попал один раз Р2 – вероятность двух попаданий.
Р0
0,42
Р2
0,49
Р1
0,09
Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет не более трех очков, равна…
Вероятность появления события А в 40 независимых испытаниях, проводимых по схеме Бернулли, равна 0,5. Тогда дисперсия числа появлений этого события равна
10
1,25
20
1
Формула Байеса имеет вид
Р(Нi/A) =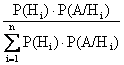 
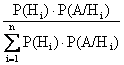
Р(Нi/A) = P(Hi)×P(A/Hi)
Р(Нi/A) =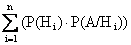 
Р(Нi/A) = P(A)×P(Hi)
Стрелок попадает в цель с вероятностью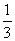 
. Стрелок стреляет три раза. Р3 – вероятность попасть три раза. Р2 – вероятность попасть два раза, один раз смазать. Р1 – вероятность попасть один раз, два раза смазать. Р0 – вероятность все три раза смазать. Выберите верные утверждения
. Стрелок стреляет три раза. Р3 – вероятность попасть три раза. Р2 – вероятность попасть два раза, один раз смазать. Р1 – вероятность попасть один раз, два раза смазать. Р0 – вероятность все три раза смазать. Выберите верные утвержденияР2 =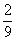 
Р0 =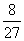 
Р1 =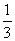
Р3 =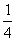 
Два стрелка стреляют по мишени. Вероятность попадания в цель у одного стрелка 0,8, у другого – 0,9. Найти вероятность того, что цель не будет поражена ни одной пулей. Ответ дайте десятичной дробью
X и Y - независимы. DX = 5, DY = 2. Используя свойства дисперсии, найдите D(2X + 3Y). Ответ дайте числом
Случайная величина X принимает значения 7, -2, 1, -5, 3 с равными вероятностями. Найдите MX. Ответ дайте десятичной дробью
Игральный кубик бросают один раз. Вероятность того, что на верхней грани выпадет число очков, большее чем четыре, равна
1/3
2/3
1
1/2
С первого станка на сборку поступает 40%, остальные 60% со второго станка. Вероятность изготовления бракованной детали для первого и второго станка соответственно равны 0,01 и 0,04. Найдите вероятность того, что наудачу пос тупившая на сборку деталь окажется бракованной. Ответ дайте десятичной дробью
Изделия изготовляются независимо друг от друга. В среднем одно изделие из ста оказывается бракованным. Чему равна вероятность того, что оба взятых наугад изделия окажутся неисправными? Ответ дайте десятичной дробью
Дан закон распределения вероятностей дискретной случайной величины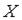 
: 
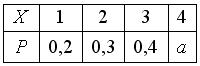Тогда значение 
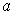равно…
: Тогда значение равно…0,7
0,2
0,1
– 0,7
Даны два множества А = {1, 2, 4, 6, 8, 10} и B = {1, 3, 6, 9}. Укажите соответствие между операциями и множествами
AÇB
{1, 2, 3, 4, 6, 8, 9, 10}
A\B
{2, 4, 8, 10}
AÈB
{1, 6}
Дискретная случайная величина Х имеет закон распределения вероятностей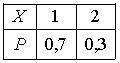 
. Математическое ожидание М(Х) этой случайной величины равно
. Математическое ожидание М(Х) этой случайной величины равно1,3
1
1,7
3
Игральный кубик бросают один раз. Вероятность того, что на верхней грани выпадет нечетное число очков, равна
1/3
1
2/3
1/2
Дискретная случайная величина Х имеет закон распределения вероятностей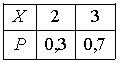 
. Математическое ожидание М(Х) этой случайной величины равно
. Математическое ожидание М(Х) этой случайной величины равно2,7
5
2,3
1
Выберите верные утверждения
0! не существует
2! = 2
0! = 1
0! = 0
Случайная величина имеет показательное распределение с плотностью { f(x) = e-x при x ³ 0; f(x) = 0 при x < 0 }. Тогда функция распределения равна
{ F(x) = 1 - e-2x при x ³ 0; F(x) = 0 при x < 0 }
{ F(x) = 1 - e-x при x ³ 0; F(x) = 0 при x < 0 }
F(x) = 1 - e-x при любом х }
{ F(x) = e-x при x ³ 0; F(x) = 0 при x < 0 }
По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию, равны 0,5 и 0,15. Тогда вероятность банкротства обоих предприятий равна
0,65
0,425
0,075
0,75
Вероятность появления события А в 40 независимых испытаниях, проводимых по схеме Бернулли, равна 0,6. Тогда дисперсия числа появлений этого события равна
24
0,96
9,6
0,15
Если Е – достоверное событие и события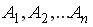 
образуют полную систему, то выполнено(ы) соотношение(я)
образуют полную систему, то выполнено(ы) соотношение(я)
= для 
для Вероятность появления события А в 20 независимых испытаниях, проводимых по схеме Бернулли, равна 0,3. Тогда дисперсия числа появлений этого события равна
0,42
0,15
6
4,2
Вероятность появления события А в 40 независимых испытаниях, проводимых по схеме Бернулли, равна 0,4. Тогда дисперсия числа появлений этого события равна
16
9,6
0,01
0,96
Вероятность наступления некоторого события не может быть равна
1
0,6
0,4
1,6
Первый студент не сдаст сессию с вероятностью 0,2; а второй - с вероятностью 0,3. Вероятность того, что они оба не сдадут сессию, равна
0,6
0,06
0,5
0,05
Два стрелка стреляют по одной мишени. Вероятность попадания первым стрелком равна 0,9. Вероятность попадания вторым стрелком равна 0,8. Р2 – вероятность попасть обоим стрелкам. Р1 – вероятность, что попал только один стрелок. Р0 – вероятность смазать обоим стрелкам. Р0,1 – вероятность первый смазал, второй попал. Выберите верные утверждения
Р0 = 0,1,
Р1 = 0,26
Р2 = 0,72
Р0,1 = 0,3
Из урны, в которой находятся 3 белых и 7 черных шаров, вынимают одновременно 2 шара. Тогда вероятность того, что оба шара будут белыми, равна…
Случайная величина имеет показательное распределение с параметром 2. Тогда ее плотность распределения
{ f(x) = 1 - e-2x при x ³ 0; f(x) = 0 при x < 0 }
{ f(x) = e-2x при x ³ 0; f(x) = 0 при x < 0 }
{ f(x) = 2e-2x при x ³ 0; f(x) = 0 при x < 0 }
{ f(x) = 2e-2x }
Случайная величина Х имеет показательное распределение с параметром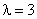 
. Тогда ее функция распределения F(x) равна
. Тогда ее функция распределения F(x) равна{ F(x) = 1 - e-3x при любом х }
{ F(x) = e-3x при x ³ 0; F(x) = 0 при x < 0 }
{ F(x) = 1 - e-x при x ³ 0; F(x) = 0 при x < 0 }
{ F(x) = 1 - e-3x при x ³ 0; F(x) = 0 при x < 0 }
В тире лежат два ружья. Вероятность стрелку попасть из первого ружья 0,6. Вероятность стрелку попасть из второго ружья 0,5. Стрелок заходит в тир, наугад берёт ружьё, три раза стреляет. Р3 – вероятность попасть три раза. Р2 – вероятность попасть два раза, один раз смазать. Р1 – вероятность попасть один раз, два раза смазать. Р0 – вероятность все три раза смазать. Выберите верные утверждения
Р3 = 0,4035
Р0 = 0,0945
Р1 = 0,3315
Р2 = 0,5035
На каждой из 4 карточек написаны по одной различной букве: Б, Е, Н, О. Из этих букв ребенок, не умеющий читать, складывает четырехзначные буквосочетания. Вероятность, того, что у него получится слово «небо», равна
0,01
Дискретная случайная величина Х задана законом распределения вероятностей 
Тогда значение интегральной функции распределения вероятностей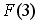 
равно …
Тогда значение интегральной функции распределения вероятностей равно …0,5
0,6
0,9
0,8
В ящике 10 лотерейных билетов. Из них два выигрышных. Наугад вынимаются два билета. Вероятность того, что оба окажутся выигрышными, равна
0,1
0,2
Вероятность наступления некоторого события не может быть равна
0,4
4
1
0
Стрелок попадает в цель с вероятностью 0,5. Стрелок стреляет три раза. Р3 – вероятность попасть три раза. Р2 – вероятность попасть два раза, один раз смазать. Р1 – вероятность попасть один раз, два раза смазать. Р0 – вероятность все три раза смазать. Выберите верные утверждения
Р1 = 0,375
Р2 = 0,375
Р0 = 0,475
Р3 = 0,1
Укажите соответствие между формулами и их значениями
1!
6
4!
24
3!
1
Имеются две одинаковые на вид урны. В первой урне находятся два белых и два черных шара. Во второй урне - четыре белых и один черный шар. Из наудачу взятой урны взяли один шар. Тогда вероятность того, что этот шар белый равна …
В урне находятся 2 белых, 1 красный, 2 зеленых и 1 черный шар. Из урны поочередно вынимают три шара, но после первого вынимания шар возвращается в урну, и шары в урне перемешиваются. Тогда значение вероятности того, что все извлеченные шары белые, равно…
Первый студент получит стипендию с вероятностью 0,9; второй – с вероятностью 0,8. Вероятность того, что оба студента будут получать стипендию, равна
0,72
0,072
1,7
0,9