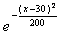Теория вероятностей, математическая статистика и случайные процессы
Абсолютный момент случайной величины Х порядка “n” определяется выражением
M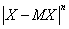
ç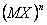
– 
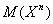ï
– ï
Дискретная случайная величина задана законом распределения вероятностей: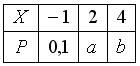 
Тогда её математическое ожидание равно 2,9 если …
Тогда её математическое ожидание равно 2,9 если …a = 0,5; b = 0,5
a = 0,3; b = 0,6
a = 0,4; b = 0,5
a = 0,6; b = 0,3
Вероятность невозможного события равна
0,0002
1
– 1
0
Условную вероятность события А при условии, что произошло событие B, можно вычислить по формуле: P(A/B) =
1 – Р(1.
1 – Р(2.
Случайная величина Х распределена по нормальному закону, её плотность вероятности f(x) =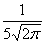 
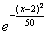. Тогда ее числовые характеристики таковы
. Тогда ее числовые характеристики таковыMX = 2; DX = 10; σX =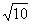 
MX = 5; DX = 2; σX =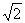 
MX = 2; DX = 25; σX = 5
MX = 5; DX = 25; σX = 2
Дискретная случайная величина Х имеет закон распределения вероятностей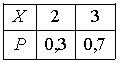 
. Математическое ожидание М(Х) этой случайной величины равно
. Математическое ожидание М(Х) этой случайной величины равно1
2,7
5
2,3
Случайная величина Х равномерно распределена на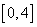 
. Тогда вероятность попасть в интервал 
будет равна
. Тогда вероятность попасть в интервал 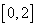будет равна0,25
0.5
0,66
0,33
Вероятность того, что при бросании одного игрального кубика выпадет число очков, кратное четырем, составляет …
4
Прибор состоит из двух элементов, работающих независимо. Вероятность вы хода из строя первого элемента при включении прибора – 0,03, второго – 0,06. Найти вероятность того, что после включения прибора исправным окажется хотя бы один элемент. Ответ дайте десятичной дробью
В урне 4 билета. Из них 2 выигрышных. Вынимаем три билета случайным образом. Р3 – вероятность вынуть три выигрышных билета. Р2 – вероятность вынуть два выигрышных билета. Р1 – вероятность вынуть один выигрышный билет. Р0 – вероятность, что все билеты не выиграли. Выберите верные утверждения
Р0 = 0,1
Р3 = 0,1
Р1 = 0,5
Р2 = 0,5
Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет не менее пяти очков, равна…
Точечная оценка математического ожидания нормального распределения равна 15. Тогда его интервальная оценка может иметь вид...
(13,8; 15)
(15; 16,2)
(13,8; 14,1)
(13,8; 16,2)
Игральный кубик бросают один раз. Вероятность того, что на верхней грани выпадет число очков, равное двум или трем, равна
2/3
1/3
1/6
1/2
В течение дня первый рыбак поймает щуку с вероятностью 0,6; а второй – с вероятностью 0,8. Вероятность того, что оба рыбака поймают по щуке, равна
1,4
0,48
0,52
0,2
Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет более трех очков, равна…
Вероятность появления события А в 20 независимых испытаниях, проводимых по схеме Бернулли, равна 0,95. Тогда математическое ожидание числа появлений этого события равно …
18,05
19
1
0,95
Вероятность стрелку попасть в мишень равна 0,9. Стрелок стреляет четыре раза. Р1 – вероятность попасть точно один раз. Р2 – вероятность попасть точно два раза. Р3 – вероятность попасть точно три раза
Р2
0,2916
Р1
0,0036
Р3
0,0486
В квадрат со стороной 13 брошена точка. 
Тогда вероятность того, что она попадет в выделенную область, равна …
Тогда вероятность того, что она попадет в выделенную область, равна …
Вероятность стрелку попасть в мишень равна 0,8. Стрелок стреляет два раза. Р0 – вероятность, что попаданий нет. Р1 – вероятность, что попал один раз Р2 – вероятность двух попаданий.
Р2
0,32
Р0
0,04
Р1
0,64
Игральный кубик бросают один раз. Вероятность того, что на верхней грани выпадет число очков, меньшее чем два, равна
5/6
1/6
1/3
2/3
Стрелок попадает в цель с вероятностью 0,5. Стрелок стреляет три раза. Р3 – вероятность попасть три раза. Р2 – вероятность попасть два раза, один раз смазать. Р0 – вероятность все три раза смазать. Выберите верные утверждения Р1 – вероятность попасть один раз, два раза смазать.
Р1 = 0,475
Р3 = 0,125
Р0 = 0,125
Р2 = 0,1
Лампочки изготовляются независимо друг от друга. В среднем одна лам почка из тысячи оказывается бракованной. Чему равна вероятность того, что из двух взятых наугад лампочек окажутся исправными обе? Ответ дайте десятичной дробью (с точностью до трех знаков после запятой)
Дискретная случайная величина Х задана законом распределения вероятностей: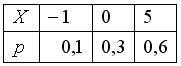 
Тогда математическое ожидание случайной величины 
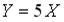равно…
Тогда математическое ожидание случайной величины равно…14,5
15,5
20
7,9
Выберите верные утверждения
0! = 0;
n! = n;
n! = n×(n-1)×(n-2)×××2×1
4! = 24
Вероятность безотказной работы каждой из 5 однотипных машин в течение заданного времени равна 0,8. Вероятность того, что по истечении заданного времени безотказно проработают две машины, а откажут три, равна
(0,8)2(0,2)3
(0,8)2(0,2)3
(0,8)2
Прибор состоит из двух элементов, работающих независимо. Вероятность выхода из строя первого элемента при включении прибора – 0,05, второго – 0,08. Найти вероятность того, что при включении прибора оба элемента будут работать Ответ дайте десятичной дробью
Вероятность стрелку попасть в мишень равна 0,9. Стрелок стреляет пять раз. Р0 – вероятность ни разу не попасть. Р1 – вероятность попасть точно один раз. Р2 – вероятность попасть точно два раза
Р0
0,0081
Р1
0,00045
Р2
0,00001
Дискретная случайная величина Х имеет закон распределения вероятностей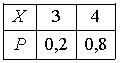 
. Математическое ожидание М(Х) этой случайной величины равно
. Математическое ожидание М(Х) этой случайной величины равно1
7
3,2
3,8
Из колоды в 32 карты извлекают одну карту. Вероятность того, что она будет красной масти, равна
0,75
0,4
0,25
0,5
В этом году хороший урожай пшеницы будет с вероятностью 0,7; а ячменя – с вероятностью 0,9. Вероятность того, что уродятся и пшеница, и ячмень, равна
0,9
0,063
0,63
1,6
В лотерее 1 000 билетов. На один билет выпадает выигрыш 5000 рублей, на десять билетов – выигрыши по 1 000 рублей, на пятьдесят билетов – выигрыши по 200 рублей, на сто билетов – выигрыши по 50 рублей; остальные билеты проигрышные. Покупается один билет. Тогда вероятность выигрыша не менее 50, но не более 200 рублей равна …
0,025
0,1
0,15
В урне находятся 2 белых, 2 красных, 2 зеленых и 4 черных шара. Из урны поочередно вынимают три шара, но после первого вынимания шар возвращается в урну, и шары в урне перемешиваются. Тогда значение вероятности того, что все извлеченные шары белые, равно …
Рулетка размечается с помощью меток – 00, 0, 1, ...36. ( Всего 38 меток). Метки при игре не имеют преимуществ друг перед другом. Игрок делает 114 попыток. Какова вероятность ни разу не выиграть? е-3 = 0,0498. Ответ дайте десятичной дробью
Из урны, в которой находятся 4 черных и 6 белых шаров, вынимают одновременно 2 шара. Тогда вероятность того, что оба шара будут черными, равна...
Центральный момент случайной величины Х порядка “n” определяется выражением
М(Х – МХ)n
(МХ)n – МХn
МХn
(МХ)n
Событие А может наступить лишь при условии появления одного из двух несовместных событи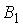й 
и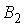 
, образующих полную группу событий. Известны вероятность 
и условные вероятности 
. Тогда вероятность 
равна …
и , образующих полную группу событий. Известны вероятность 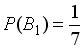и условные вероятности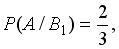 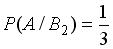. Тогда вероятность 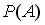равна …
Вратарь парирует в среднем 0.3 всех одиннадцатиметровых штрафных ударов. Какова вероятность того, что он возьмет ровно 2 из 4 одиннадцатиметровых? Ответ дайте десятичной дробью
Случайная величина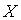 
распределена равномерно на отрезке
.. Тогда случайная величина 
имеет…
распределена равномерно на отрезке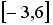.. Тогда случайная величина 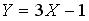имеет…равномерное распределение на отрезке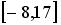 
равномерное распределение на отрезке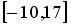 
нормальное распределение на отрезке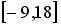 
другой (кроме равномерного и нормального) вид распределения
Два стрелка производят по одному выстрелу. Вероятность попадания в цель для первого и второго стрелков равны 0,8 и 0,9 соответственно. Тогда вероятность того, что цель будет поражена, равна …
0,28
0,98
0,72
0,998
Пусть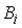 
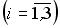- события, заключающиеся в том, что произошел обрыв в цепи сопротивлений 
, 
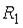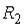или 
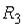
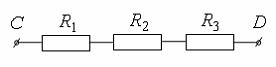Событие 
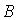- за время 
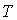произошел обрыв между точкам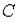и 
и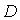 
. Тогда 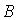представимо через 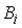следующим образом …
- события, заключающиеся в том, что произошел обрыв в цепи сопротивлений , или Событие - за время произошел обрыв между точками и . Тогда представимо через следующим образом …
В первой урне 5 белых и 5 черных шаров. Во второй урне 3 черных и 7 белых шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна…
0,12
0,65
0,1
0,6
Из каждой из двух колод вынимают по одной карте. События А – «карта из первой колоды – красной масти» и В – «карта из второй колоды – бубновой масти» являются:
Совместными
зависимыми
несовместными
независимыми
Имеются две одинаковые на вид урны. В первой урне находятся один белый и два черных шара. Во второй урне - два белых и два черных шара. Из наудачу взятой урны взяли один шар. Тогда вероятность того, что этот шар белый равна …
Стрелок попадает в цель с вероятностью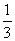 
. Стрелок стреляет три раза. Р3 – вероятность попасть три раза. Р2 – вероятность попасть два раза, один раз смазать. Р1 – вероятность попасть один раз, два раза смазать. Р0 – вероятность все три раза смазать. Выберите верные утверждения
. Стрелок стреляет три раза. Р3 – вероятность попасть три раза. Р2 – вероятность попасть два раза, один раз смазать. Р1 – вероятность попасть один раз, два раза смазать. Р0 – вероятность все три раза смазать. Выберите верные утвержденияР2 =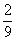 
Р3 =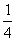 
Р0 =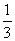
Р1 =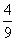 
Укажите соответствие между формулами и их значениями
3
1
2
В круг радиусом 20 вписан меньший круг радиусом 10 так, что их центры совпадают. Найти вероятность того, что точка, наудачу брошенная в большой круг, попадет также и в кольцо, образованное построенными окружностями. Предполагается, что вероятность попадания точки в круг пропорциональна площади круга и не зависит от его расположения Ответ дайте десятичной дробью
Футбольная команда выиграет первый матч с вероятностью 0,9; а второй – с вероятностью 0,4. Вероятность того, что команда выиграет оба матча, равна
0,5
0,36
1,3
0,64
В урне находятся 4 белых и 8 красных шаров. Наугад извлекается один шар. Вероятность того, что он красного цвета, равна
0,5
0,125
В группе 25 студентов, из которых отлично учится 5 человек, хорошо - 12, удовлетворительно - 6 и плохо - 2. Преподаватель вызывает студента. Ка кова вероятность того, что вызванный студент или отличник или хорошист? Ответ дайте в виде обыкновенной дроби a/b
Случайная величина Х распределена по нормальному закону. Математическое ожидание и среднеквадратическое отклонение этой случайной величины соответственно равны 30 и 10. Плотность распределения Х имеет вид
f(x) =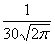 
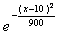
f(x) =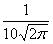 
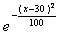
f(x) =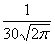 
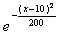
f(x) = 