Теория вероятностей, математическая статистика и случайные процессы
Игральный кубик бросают один раз. Вероятность того, что на верхней грани выпадет число очков, кратное четырем, равна
0
5/6
1/2
1/6
В среднем каждое сотое изделие, производимое предприятием, дефектное. Если взять 2 изделия, какова вероятность, что оба окажутся исправными? Ответ дайте десятичной дробью (с точностью до трех знаков после запятой)
Даны два множества А = {1, 2, 4, 6, 8, 10} и B = {1, 5, 10, 15}. Укажите соответствие между операциями и множествами
A È B
{2, 4, 6, 8}
A Ç B
{1, 10}
A \ B
{1, 2, 4, 5, 6, 8, 10, 15}
Функция распределения случайной величины F(x) выражается через ее плотность распределения f(x) следующим образом
F(x) =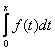 
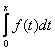
F(x) =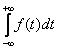
F(x) =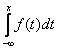 
F(x) =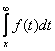
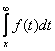
Тогда математическое ожидание случайной величины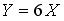 
равно…
равно…7,8
6,6
6
7,1
Вероятность наступления некоторого события не может быть равна
0,2
0
1,2
0,8
Первый завод выпускает качественные станки с вероятностью 0,9; а второй – с вероятностью 0,8. На каждом заводе купили по одному станку. Вероятность того, что оба они качественные, равна
1
0,28
0,72
1,6
Вероятность появления события А в 40 независимых испытаниях, проводимых по схеме Бернулли, равна 0,9. Тогда дисперсия числа появлений этого события равна
0,36
3,6
36
2,25
Вероятность появления события А в 20 независимых испытаниях, проводимых по схеме Бернулли, равна 0,5. Тогда дисперсия числа появлений этого события равна
10
5
2,5
0,5
Вероятность попадания непрерывной случайной величины в интервал (a, b) выражается через плотность распределения следующей формулой
P (a < X < b) = f(b) – f(a)
P (a < X < b) =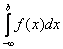 
P (a < X < b) =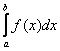 
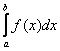
P (a < X < b) =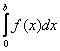 
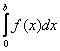
Если события А и В несовместны, то для них справедливо равенство
Р(А + 2. = Р(1. + Р(2.
Р(1. + Р(2. = 1
Р(А + 2. = Р(1. ×Р(2.
Р(А/B) = 1
На первой полке 12 книг, из которых 4 на русском языке. На второй полке 10 книг, из которых 5 на русском языке. С каждой полки выбирается по одной книге. Вероятность того, что хотя бы одна из книг будет на русском языке, равна
+ 
+ – 
0,5
0,6
Вероятность того, что студент сдаст экзамен, равна 0,8. Тогда вероятность того, что студент сдаст хотя бы один из 3 экзаменов сессии, равна …
0,128
0,008
0,333
0,992
Игральный кубик бросают один раз. Вероятность того, что на верхней грани выпадет число очков, кратное четырем, равна
5/6
1/2
1/6
0
По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию, равны 0,5 и 0,05. Тогда вероятность банкротства обоих предприятий равна
0,25
0,55
0,475
0,025
Квантиль распределения Кр уровня Р непрерывной случайной величины с функцией распределения F(x) определяется как решение уравнения
F(p) = p×Kp
F(Kp) = P
F(p) = Kp
F(Kp) = P2
Дискретная случайная величина задана законом распределения вероятностей: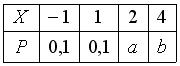 
Её математическое ожидание равно 2,2 если …
Её математическое ожидание равно 2,2 если …a = 0,3, b = 0,5
a = 0,5, b = 0,3
a = 0,6, b = 0,2
a = 0,9, b = 0,2
В квадрат со стороной 7 вписан круг.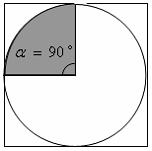 
Тогда вероятность того, что точка, брошенная в квадрат, попадет в выделенный сектор, равна …
Тогда вероятность того, что точка, брошенная в квадрат, попадет в выделенный сектор, равна …
Баскетболист попадает в корзину мячом с вероятностью 0,7. Вероятность из пяти бросков три раза попасть и два раза смазать равна
(0,7)3
(0,7)3×(0,3)2
×(0,7)3×(0,3)2Математическое ожидание дискретной случайной величины – это
По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию, равны 0,5 и 0,25. Тогда вероятность банкротства обоих предприятий равна
0,75
0,125
0,375
0,105
Вероятность невозможного события равна
0,002
1
– 1
0
Дискретная случайная величина Х задана законом распределения вероятностей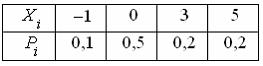 
Тогда значение интегральной функции распределения вероятностей 
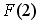равно …
Тогда значение интегральной функции распределения вероятностей равно …0,1
0,6
0,5
0,8
В квадрат со стороной 6 брошена точка. 
Тогда вероятность того, что она попадет в выделенную область, равна …
Тогда вероятность того, что она попадет в выделенную область, равна …
3
Случайная величина Х называется центрированной, если
DX = 1
MX = 1
DX = MX
МХ = 0
Случайная величина имеет показательное распределение с математическим ожиданием, равным 7. Плотность вероятности такой величины равна
{ f(x) = 0 при x < 0; f(x) =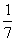 
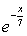при х ³ 0 }
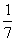
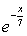при х ³ 0 }{ f(x) = при любых х }
при любых х }{ f(x) = 0 при x < 0; f(x) = 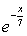при х ³ 0 }
при х ³ 0 }{ f(x) = 0 при x < 0; f(x) = 7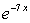
при х > 0 }
при х > 0 }В колоде 32 карты. Вынимаем две карты. Р0 – вероятность, что тузов нет. Р1 – вероятность, что вынут один туз. Р2 – вероятность, что вынуты два туза
Р2
Р1
Р0
Три шарика случайным образом помещают в трех ящиках. Вероятность того, что в каждом ящике окажется по одному шарику, равна
0,5
Два стрелка стреляют по одной мишени. Вероятность попадания первым стрелком равна 0,9. Вероятность попадания вторым стрелком равна 0,8. Р2 – вероятность попасть обоим стрелкам. Р1 – вероятность, что попал только один стрелок. Р0 – вероятность смазать обоим стрелкам. Р0,1 – вероятность первый смазал, второй попал. Выберите верные утверждения
Р0,1 = 0,3
Р2 = 0,72
Р0 = 0,02
Р1 = 0,17
В ящике лежит 8 деталей из которых 2 бракованных. Наудачу берут две. Тогда вероятность того, что среди них ровно одна бракованная, равна …
Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет менее трех очков, равна…
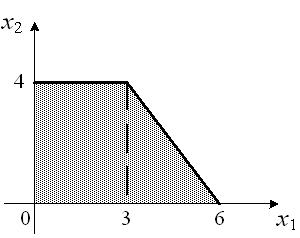Тогда максимальное значение функции 
равно…20
26
28
23
Вероятность достоверного события равна
0,997
– 1
1
0
Область допустимых решений задачи линейного программирования имеет вид: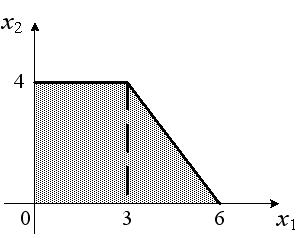 
Тогда максимальное значение функции 
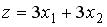равно…
Тогда максимальное значение функции равно…18
23
21
20
Стрелок попадает в цель с вероятностью 0,5. Стрелок стреляет три раза. Р3 – вероятность попасть три раза. Р2 – вероятность попасть два раза, один раз смазать. Р1 – вероятность попасть один раз, два раза смазать. Р0 – вероятность все три раза смазать. Выберите верные утверждения
Р1 = 0,375
Р2 = 0,1
Р0 = 0,475
Р3 = 0,125
Пусть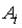 
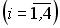- события, заключающиеся в том, что в электрической цепи 
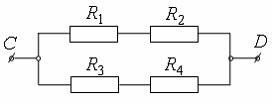сопротивления 
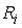не вышли из строя за время 
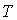, событие 
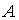- цепь из строя не вышла за время 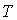. Тогда 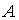представимо через 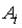следующим образом …
- события, заключающиеся в том, что в электрической цепи сопротивления не вышли из строя за время , событие - цепь из строя не вышла за время . Тогда представимо через следующим образом …
Если события А, В, С независимы, то
Р(А×В×3. = Р(1. ×Р(2. ×Р(3.
Р(А + В + 3. = Р(1. ×Р(2. ×Р(3.
Р(А×В×3. = Р(1. + Р(2. + Р(3.
Р(А + В + 3. = Р(1. + Р(2. + Р(3.
График плотности вероятностей для нормального распределения изображен на рисунке
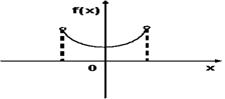
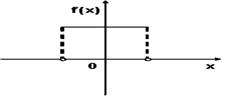
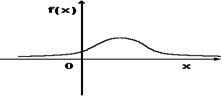
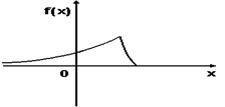
Среднеквадратическое отклонение произведения случайной величины Х на постоянную С равно
σ(CX) = C + σ(X)
σ(CX) = êC ê× σ(X)
σ(CX) = C2×σ(X)
σ(CX) =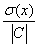 
График плотности распределения вероятностей непрерывной случайной величины Х, распределённой равномерно в интервале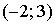 
, имеет вид: 
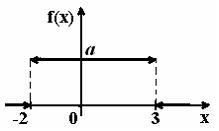Тогда значение а равно
, имеет вид: Тогда значение а равно0,25
1
0,5
0,2
Вероятность невозможного события равна
0,5
любому числу меньше нуля
0,1
0
Дискретная случайная величина Х имеет закон распределения вероятностей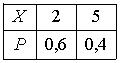 
. Математическое ожидание М(Х) этой случайной величины равно
. Математическое ожидание М(Х) этой случайной величины равно3,2
3,8
7
1
График плотности распределения вероятностей непрерывной случайной величины Х, распределённой равномерно в интервале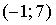 
, имеет вид: 
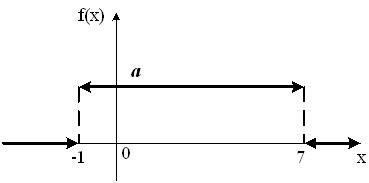Тогда значение a равно
, имеет вид: Тогда значение a равно
1
В квадрат со стороной 14 брошена точка. 
Тогда вероятность того, что она попадет в выделенную область, равна …
Тогда вероятность того, что она попадет в выделенную область, равна …
7
Игральная кость бросается один раз. Тогда вероятность того, что выпадает число очков, равное 3, равна
0,1
0,2
Случайная величина Х имеет распределение Пуассона с параметром l = 9. Ее числовые характеристики равны
MX = 3; DX = 3 σX =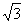 
MX = 3; DX = 9 σX = 3
MX = 9; DX = 81 σX = 9
MX = 9; DX = 9 σX = 3
В урне 20 шаров: 10 красных, 7 белых, 3 чёрных. Студент берёт наугад шар. Рк – вероятность вынуть красный шар, Рб – вероятность вынуть белый шар, Рч – вероятность вынуть чёрный шар
Рч
0,35
Рк
0,5
Рб
0,15
Вероятность стрелку попасть в мишень равна 0,9. Стрелок стреляет четыре раза. Р0 – вероятность ни разу не попасть. Р1 – вероятность попасть один раз. Р2 – вероятность попасть два раза
Р2
0,0036
Р0
0,0001
Р1
0,0486
Вероятность появления события А в 10 независимых испытаниях, проводимых по схеме Бернулли, равна 0,5. Тогда дисперсия числа появлений этого события равна
0,05
0,25
2,5
5
Укажите соответствие между формулами и их значениями
3!
120
4!
24
5!
6