Математический анализ (курс 3)
Общее решение уравнения ut + aux = 0, где С - произвольная функция, записывается в виде
u(x,t) = C(x-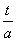 )
)
u(x,t) = C(x+at)
u(x,t) = C1(x-at) + C2(x+at)
u(x,t) = C(x-at)
Главная часть лорановского разложения функции 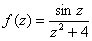 в проколотой окрестности точки 2i
в проколотой окрестности точки 2i
содержит только два члена
содержит только один член
содержит бесконечно много ненулевых членов
отсутствует
Ряд 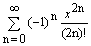 есть разложение в ряд Маклорена функции
есть разложение в ряд Маклорена функции
sin х на всей числовой оси
ех на всей числовой оси
cos x на всей числовой оси
ln (1 + х) на промежутке -1 < x £ 1
Высказывание, которое истинно тогда и только тогда, когда истинны оба составляющих его высказывания, является их
означает их эквивалентность
импликацией
дизъюнкцией
конъюнкцией
При делении числа 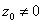 на 2
на 2
модуль числа z0 делится на 2, аргумент уменьшается на 2
модуль числа z0 делится на 2, аргумент не меняется
и модуль, и аргумент числа z0 делятся на 2
аргумент числа z0 делится на 2, а модуль не меняется
Модуль  в некоторой точке равен
в некоторой точке равен
средней кривизне
кривизне кривой в этой точке
единице
кручению в этой точке
Для функции 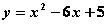 точка М (3, - 4) является точкой
точка М (3, - 4) является точкой
разрыва
минимума
максимума
перегиба
{x: -1 £ х £ 1}, B = {y: 0 £ y £ 1}. Соответствие, заданное формулой : y = x2 является взаимно однозначным при
х Î (-1,1)
х Î [0,1]
х Î (0,1)
х Î [-1,1]
Коэффициент ряда Фурье элемента f(x) = x по ортогональной системе 1, coskx, sinkx, k = 1,2,… пространства L2[-p,p] при sin2x равен
-2
-1
3
2
Коэффициент В(l) в задаче Коши для уравнения теплопроводности Ut = Uxx, U(x,0) = j(x) вычисляется по формуле В(l) = 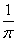
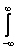 j(x)sinx
j(x)sinx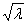 dx Тогда коэффициент B(l) при U(x,0) = j(x) =
dx Тогда коэффициент B(l) при U(x,0) = j(x) = 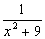 равен
равен
0
1
Бесконечно убывающей геометрической прогрессией называют такую, у которой знаменатель q удовлетворяет условию
|q| <1
q < 1
|q| >1
|q| = 1
Положение точки 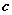 , о которой говорится в теоремах Лагранжа, Ролля, Коши, находится
, о которой говорится в теоремах Лагранжа, Ролля, Коши, находится
в точке 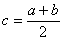
на середине отрезка 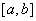
где-то между 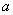 и
и 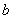 :
: 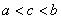
в одном из концов интервала
Последовательность может иметь
только один предел
два различных предела
не больше двух разных пределов
любое количество пределов
Наилучшее линейное приближение функции x3 в пространстве L2[-1,1] равно
0,6x
0,4x
1 + 0,6x
1 + 0,4x
Единичный касательный вектор 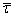 в точке t0 = 0 кривой M(t) = (t2,t,1-t3) будет
в точке t0 = 0 кривой M(t) = (t2,t,1-t3) будет
Решение уравнения колебания струны Utt = a2Uxx с начальным отклонением U(x,0) = j(x) и начальной скоростью Ut(x,0) = y(x) записывается в виде U(x,t) = 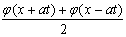 +
+ 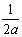
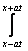 y(x)dx Тогда решение уравнения Utt = 16Uxx при начальном отклонении U(x,0) = х2 и начальной скоростью Ut (x,0) = 0 имеет вид
y(x)dx Тогда решение уравнения Utt = 16Uxx при начальном отклонении U(x,0) = х2 и начальной скоростью Ut (x,0) = 0 имеет вид
U(x,t) = 2x2 + t2 ;
U(x,t) = x2 - 16t2 ;
U(x,t) = x2 + 2t2 ;
U(x,t) = x2 + 16t2 ;
Косинус угла между элементами f(x) и g(x) в пространстве L2 [a,b] определяется по формуле: cos(f(x),g(x)) = 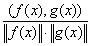 ; (f(x),g(x)) =
; (f(x),g(x)) = 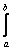 f(x)×g(x)dx ;
f(x)×g(x)dx ; 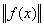 =
= 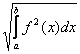 .Тогда косинус угла между элементами x4 и 1 в пространстве L2 [0,2] равен
.Тогда косинус угла между элементами x4 и 1 в пространстве L2 [0,2] равен
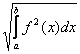 .Тогда косинус угла между элементами x4 и 1 в пространстве L2 [0,2] равен
.Тогда косинус угла между элементами x4 и 1 в пространстве L2 [0,2] равен-0,5
-0,1
0,8
0,6
Уравнение 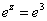
имеет бесконечное множество решений 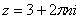 ,
, 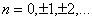
имеет единственное решение 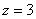
имеет единственное решение 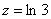
имеет решения, отличные от 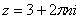 ,
, 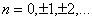 ,
, 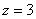 ,
, 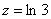
Ряд 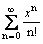 есть разложение функции
есть разложение функции
ех на всей числовой прямой
sin x на всей числовой прямой
ln (1 + x) на промежутке -1 < x £ 1
ех только на интервале (-1,1)
Даны два утверждения: 1) уравнение (Uz)2 - (Uy)2 + U2 = 0 нелинейное, 2) уравнение Uxx + Uуy + Uzz = U однородное. Утверждения
первое неверно, второе верно
оба неверны
первое верно, второе неверно
оба верны
Пространственная кривая задана параметрическими уравнениями 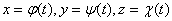 . Ее векторным уравнением будет
. Ее векторным уравнением будет
Площадь области, ограниченной линиями 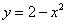 и
и 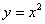 , вычисляется с помощью определенного интеграла
, вычисляется с помощью определенного интеграла
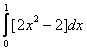
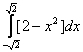
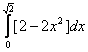
Для функции 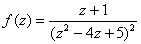 точка
точка 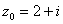
является полюсом четвертого порядка
особой точкой не является
является существенно особой точкой
является полюсом второго порядка
Уравнение 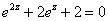
имеет бесконечно много решений
не имеет решений
имеет 2 решения
имеет 1 решение
Предел 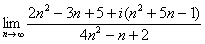
существует и равен 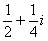
не существует
существует и равен 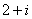
существует и равен 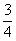
Даны два утверждения: 1) уравнение yUxx + xUyy - z2Uzz = 0 имеет второй порядок, 2) уравнение y2Uxy - x2Uzx + z2Uzy = 0 имеет второй порядок. Утверждения
первое неверно, второе верно
оба неверны
первое верно, второе неверно
оба верны
Функции U1 = x + y2 и U2 = e2xy являются решениями уравнения
yUxx + Uyy - 2Ux = 0
Uxx + Uyy - e-2xUy = 0
Uxx + Uyy - 2Ux = 0
Uxx + Uyy = 0
Если 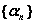 и
и 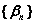 - бесконечно малые последовательности
- бесконечно малые последовательности 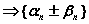 последовательность
последовательность
большего порядка малости
меньшего порядка малости
бесконечно малая
бесконечно большая
Эллиптический тип имеет уравнение
5Uxx + 2Uxy - Uyy = 0
3Uxx + 4Uyy = 0
Uxx + 2Uxy + Uyy = 0
3Uxx - Uyy = 0
Функция 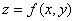 называется дифференцируемой в точке
называется дифференцируемой в точке 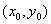 , если
, если
имеет частные производные 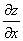 и
и 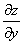
имеет частные производные 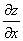 и
и 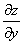 в этой точке
в этой точке
Норма В интегрального оператора Фредгольма с ядром К(t,s) в пространстве L2[a,b] определяется по формуле В = 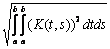 Тогда норма интегрального оператора Фредгольма с ядром К(t,s) = t3s4 в пространстве L2[0,1] равна
Тогда норма интегрального оператора Фредгольма с ядром К(t,s) = t3s4 в пространстве L2[0,1] равна
Кривая L (x = t2 - 2t + 3, y = t2 - 2t + 1) проходит через точку
(2, 3)
(3, 1)
(2, 1)
(3, -1)
Ряд 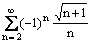
расходится
расходится абсолютно
сходится абсолютно
сходится условно
Действительные числа - это
числа, которые действительно существуют
целые числа
положительные числа
рациональные и иррациональные, положительные и отрицательные числа и число нуль
Преобразование Фурье F[f] функций удовлетворяет свойству линейности
F[K1f × K2g] = K1F[f] × K2F[g]
F[K1f × K2g] = K1F[f] + K2F[g]
F[K1f + K2g] = K1F[f] + K2F[g]
F[K1f + K2g] = K1F[f] × K2F[g]
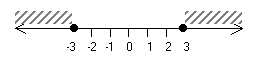
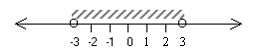

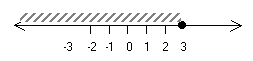
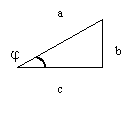 отношение b/a - это:
отношение b/a - это: