Математический анализ (курс 3)
Из функций: 1) 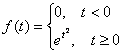 ; 2)
; 2) 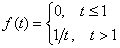 - функциями-оригиналами являются
- функциями-оригиналами являются
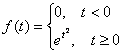 ; 2)
; 2) ни одна из 1), 2)
только 2)
только 1)
и 2)
Уравнение соприкасающейся плоскости к кривой y = y(x), z = z(x) в точке (x0, y0 = y(x0), z0 = z(x0)) определяется по формуле l(x - x0) + m(y - y0) + n(z - z0) = 0 , где l = y¢(x0)z²(x0) - y²(x0)z¢(x0) ; m = - z²(t0) ; n = y²(t0) Тогда уравнение соприкасающейся плоскости к кривой y(х) = 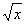 , z(x) = x2 в точке (1,1,1) имеет вид
, z(x) = x2 в точке (1,1,1) имеет вид
7x - 8y - z + 3 = 0 ;
6x - 5y - z + 3 = 0 ;
6x - 8y - z + 3 = 0 ;
6x - 8y - 2z + 3 = 0 ;
Собственными значениями матрицы системы уравнений 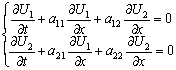 называются корни уравнения второго порядка
называются корни уравнения второго порядка 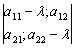 = 0 Тогда собственными значениями матрицы системы уравнений
= 0 Тогда собственными значениями матрицы системы уравнений 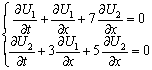 являются значения
являются значения
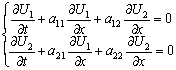 называются корни уравнения второго порядка
называются корни уравнения второго порядка 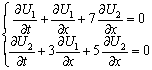 являются значения
являются значенияl1 = -1 ; l2 = 1 ;
l1 = 3 ; l2 = -5 ;
l1 = -2 ; l2 = 8 ;
l1 = -1 ; l2 = 3 ;
Область, в которой уравнение 2Uxx + yUхy - xUyy = 0 имеет гиперболический тип, расположена
внутри параболы у2 = 8х
вне параболы у2 = 8х
вне параболы у2 = - 8х
внутри параболы у2 = - 8х
Решение уравнения колебания струны Utt = a2Uxx с начальным отклонением U(x,0) = j(x) и начальной скоростью Ut(x,0) = y(x) записывается в виде U(x,t) = 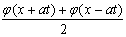 +
+ 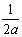
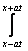 y(x)dx Тогда решение уравнения Utt = а2Uxx при начальном отклонении U(x,0) = 0 и начальной скоростью Ut (x,0) = х имеет вид
y(x)dx Тогда решение уравнения Utt = а2Uxx при начальном отклонении U(x,0) = 0 и начальной скоростью Ut (x,0) = х имеет вид
U(x,t) = xt ;
U(x,t) = xt2 ;
U(x,t) = x2t2 ;
U(x,t) = xt3 ;
Уравнение теплопроводности на плоскости имеет вид
Ut= a2(Uxx + Uyy)
Utt = a2Uxx
Uxx = a2Uyy
Uxx - Ux = 0
Связка высказываний а и b типа «а тогда и только тогда, когда b» называется
конъюнкцией а и b
импликацией а и b
эквиваленцией а и b
дизъюнкцией а и b
Граница множества 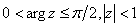 состоит из
состоит из
окружности радиуса 1 с центром в начале координат
интервала 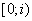 мнимой оси
мнимой оси
отрезка 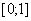 действительной оси и дуги окружности радиуса 1 с центром в начале координат
действительной оси и дуги окружности радиуса 1 с центром в начале координат
отрезка 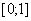 действительной оси, отрезка
действительной оси, отрезка 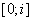 мнимой оси и дуги окружности радиуса 1 с центром в начале координат, расположенной в I четверти
мнимой оси и дуги окружности радиуса 1 с центром в начале координат, расположенной в I четверти
Последовательность  является б.м. потому, что
является б.м. потому, что
Высказывание, которое ложно тогда и только тогда, когда а - истинно, а b - ложно, является их
дизъюнкцией
означает их эквивалентность
конъюнкцией
импликацией
Ряд 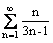
расходится, так как предел общего члена не равен нулю
сходится, так как выполняется необходимое условие сходимости ряда
сходится, так как предел общего члена меньше 1
сходится, так как предел общего члена не равен нулю
Одна из точек пересечения кривых L1 (x = t, y= 1 + t2) и L2 (x = t2, y = t + 1) будет
(0, 3)
(1, 3)
(1, 2)
(1, 0)
Решение уравнения колебания струны Utt = a2Uxx с начальным отклонением U(x,0) = j(x) и начальной скоростью Ut(x,0) = y(x) записывается в виде U(x,t) = 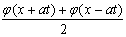 +
+ 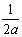
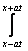 y(x)dx Тогда решение уравнения Utt = 4Uxx при начальном отклонении U(x,0) = х2 и начальной скоростью Ut (x,0) = 0 имеет вид
y(x)dx Тогда решение уравнения Utt = 4Uxx при начальном отклонении U(x,0) = х2 и начальной скоростью Ut (x,0) = 0 имеет вид
U(x,t) = 2x2 + t2 ;
U(x,t) = x2 + 2t2 ;
U(x,t) = x2 - 4t2 ;
U(x,t) = x2 + 4t2 ;
Функция U1 - решение линейного однородного уравнения LU = 0, функция U2 - решение неоднородного уравнения LU = sinxy. Тогда решением второго уравнения будет также функция
U1 - U2
U1 + 2U2
2U1 + U2
2U1 + 2U2
Преобразованием Фурье функции f(x) называется функция вида
F(s) =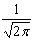
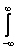 f(x)sinsdx
f(x)sinsdx
F(s) =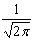
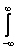 f(x)e-xsdx
f(x)e-xsdx
F(s) =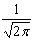
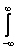 f(x)e-ixsdx
f(x)e-ixsdx
F(s) =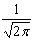
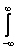 f(x)cos(sx)dx
f(x)cos(sx)dx
Даны два утверждения: 1) уравнение у3Uху + x3Uуz - z3Uzz = U линейное неоднородное, 2) уравнение (Uzz)2 - x2(Uу)2 + y2(Ux)2 = 0 имеет второй порядок. Утверждения
первое верно, второе неверно
оба неверны
оба верны
первое неверно, второе верно
Параметрические уравнения кривой линии L называются натуральными, если
за параметр принимается длина дуги S, отсчитываемая от некоторой зафиксированной точки до текущей по кривой точки M
это векторное уравнение
кривая - годограф векторной функции
за параметр берется длина кривой
Значение вектор - функции 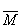 (t) = (
(t) = (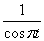 , arc tgt) в точке t0=1 - это вектор, равный
, arc tgt) в точке t0=1 - это вектор, равный
(1, -1)
(-1, 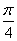 )
)
(1, 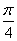 )
)
(-1, 1)
Для следующих из функций 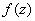 : а)
: а)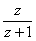 ; b)
; b) 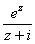 ; с)
; с)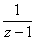 интеграл
интеграл 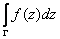 по любому замкнутому контуру
по любому замкнутому контуру 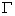 , лежащему в области
, лежащему в области 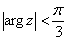 , равен нулю
, равен нулю
для а) и b)
для b) и с)
для а), b) и с)
ни для одной из них
Для системы 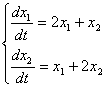 характеристическое уравнение имеет вид
характеристическое уравнение имеет вид
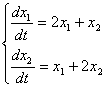 характеристическое уравнение имеет вид
характеристическое уравнение имеет видl2 - 4l - 5 = 0
l2 - 4l + 3 = 0
l2 + 4l + 3 = 0
4l2 - 1 = 0
Переменная величина y есть функция переменной величины x, если
каждому значению y отвечает определенное значение x
между значениями величин x и y установлено взаимно однозначное соответствие
каждому значению x по некоторому правилу поставлено в соответствие определенное значение y
каждому значению x отвечает определенное значение y и каждому значению y отвечает некоторое определенное значение x
Значение вектор - функции 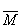 (t) = (
(t) = (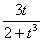 ,
, 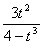 ) в точке t0 = -2 - это вектор, равный
) в точке t0 = -2 - это вектор, равный
(1, 1)
(-1, -1)
(-1, 1)
(1, -1)
Высказывание 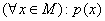 можно прочитать
можно прочитать
существует х из М такое, что р(х)
не существует такого х из М, что р(х)
всякий элемент х множества М обладает свойством р(х)
не для всякого х из М верно р(х)
Множеством истинности для высказывания |x| < 1 является
(-1, 1)
(-¥, -1)
[-1, 1]
(- ¥, 1)
Числовая ось - это прямая, на которой
отсчитываются длины
выбрано начало отсчета, установлены направление и единица измерения длин
установлено направление
выбрано начало отсчета
Уравнение 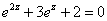
не имеет решений
имеет бесконечно много решений
имеет 1 решение
имеет 2 решения
Площадь параболического сегмента, ограниченного параболой 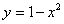 и осью Ox, равна
и осью Ox, равна
2
1
Функция у = sin2px является решением краевой задачи
y¢¢ + 4p2y = 0, y(0) = y¢(1) = 0
y¢¢ + 4y = 0, y(0) = y(2) = 0
y¢¢ + 4p2y = 0, y(0) = y(2) = 0
y¢¢ + 4y = 0, y(0) = y¢(1) = 0
Между точками на числовой оси и действительными числами установлено соответствие
служащее для изображения рациональных чисел
однозначное
взаимно однозначное
служащее для изображения целых чисел
δ -окрестностью точки 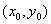 на плоскости называется
на плоскости называется
круг радиуса δ
замкнутый круг радиуса δ
замкнутый круг
круг с центром в 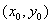 и радиуса δ, причем окружность круга не относится к δ-окрестности
и радиуса δ, причем окружность круга не относится к δ-окрестности
Значение первой производной вектор-функции M(t) = (2t, lnt, t2) в точке t0 = 1 будет
M¢(1) = (2,2,1)
M¢(1) = (1,2,1)
M¢(1) = (2,1,1)
M¢(1) = (2,1,2)