Математический анализ (курс 3)
Производная 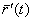 векторной функции
векторной функции 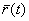 при
при 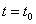 направлена по
направлена по
нормали к линии
касательной прямой в точке 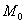
касательной прямой
касательной прямой к годографу функции 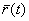 , проведенной в точке
, проведенной в точке 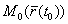
Норма элемента f(x) в пространстве С [a,b] определяется по формуле: 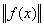 =
= 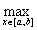
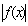 . Тогда норма элемента 2x3 - 9x2 + 12x + 1 в пространстве С [0,2] равна:
. Тогда норма элемента 2x3 - 9x2 + 12x + 1 в пространстве С [0,2] равна:
5
4
6
7
Функция 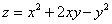
имеет экстремум в точке (0, 0)
имеет минимум, равный 0
не имеет экстремума
имеет максимум, равный 0
Даны два утверждения: 1) уравнение Uху + U2 + xUx = 0 имеет второй порядок, 2) уравнение xUx + yUу + zU - 1 = 0 линейное однородное. Утверждения
оба неверны
первое верно, второе неверно
первое неверно, второе верно
оба верны
Число 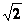 изображается десятичной дробью
изображается десятичной дробью
периодической
бесконечной непериодической
конечной
бесконечной
Наибольшая скорость возрастания функции 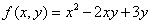 при переходе через точку (1, 2) равна
при переходе через точку (1, 2) равна
1
Теорема существования и единственности решения задачи Коши для дифференциального уравнения 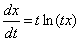 выполняется в области
выполняется в области
{-∞ < t, x <+ ∞}
{tx>0}
{ t, x <+ ∞}
{t>0, x>0}
Функцию 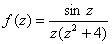 можно разложить в ряд Лорана по целым степеням z
можно разложить в ряд Лорана по целым степеням z
в кольцах 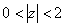 и
и 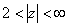
только в кольце 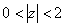
в круге 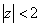
в кольце 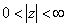
Порядком дифференциального уравнения называется
наивысшая степень функций, входящих в уравнение
наивысшая степень производных, входящих в уравнение
наивысшая степень переменных, входящих в уравнение
наивысший порядок производных, входящих в уравнение
Для того, чтобы функция 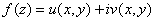 была дифференцируемой в точке
была дифференцируемой в точке 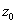 необходимо и достаточно, чтобы функции
необходимо и достаточно, чтобы функции 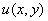 и
и 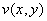 были дифференцируемыми в точке
были дифференцируемыми в точке 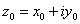 и чтобы в этой точке выполнялись условия
и чтобы в этой точке выполнялись условия
Банк выплачивает по 7% годовых. Клиент этого банка снял со своего счета через год свою прибыль - 140 тыс. рублей. Им было положено в банк _______ руб.
2000000
200000
1000000
2200000
Точка M0(-1,-1) принадлежит кривой
(x = t3 - 2t ; y = t2 - 2)
(x = 1 + 2t3 , y = t2 - t)
(х = t3 ; y = t +1)
(x = t ; y = t2 + 1)
Найти единичный вектор 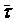 касательной к кривой x = t, y = t2, z = t3 в точке t = 1
касательной к кривой x = t, y = t2, z = t3 в точке t = 1
Изолированная конечная особая точка z0 функции 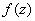 является полюсом тогда и только тогда, когда главная часть лорановского разложения
является полюсом тогда и только тогда, когда главная часть лорановского разложения 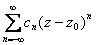
содержит хотя бы один коэффициент, отличный от нуля
имеет бесконечно много отличных от нуля коэффициентов cn
имеет лишь конечное (и положительное) число отличных от нуля коэффициентов cn
отсутствует
Функцию 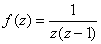 можно разложить в ряд Лорана
можно разложить в ряд Лорана 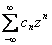
в кольцах 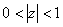 и
и 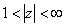
только в кольце 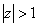
в круге 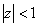
только в кольце 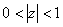
Многочлены Лежандра: Р0 = 1, Р1(х) = х, Р2 = 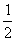 (3х2 - 1) Разложение элемента f(x) = 3x2 +5x +1 по многочленам Лежандра имеет вид:
(3х2 - 1) Разложение элемента f(x) = 3x2 +5x +1 по многочленам Лежандра имеет вид:
f(x) = 5P0 + 2P1 + 5P2
f(x) = 3P0 + 5P1 + P2
А) f(x) = 2P0 + 5P1 + 2P2
f(x) = P0 + 3P1 + 5P2
Число a есть предел функции 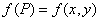 в точке
в точке 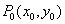 , если
, если
значения функции 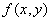 находятся в
находятся в 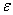 -окрестности a
-окрестности a
выполняется условие 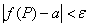
для 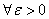 найдется
найдется 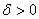 такое, что в любой точке P, принадлежащей области определения функции и попадающей в
такое, что в любой точке P, принадлежащей области определения функции и попадающей в 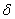 -окрестность
-окрестность 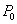 (кроме, быть может, самой точки
(кроме, быть может, самой точки 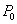 ) выполняется неравенство
) выполняется неравенство 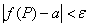 . Запись
. Запись 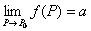
Коэффициенты A и B в формуле для полного приращения дифференцируемой в точке 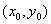 функции
функции 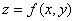 равны
равны
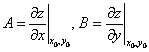
произвольным числам
A и B - б.м. высшего порядка относительно 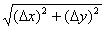
Ряд Тейлора 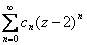 функции
функции 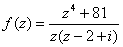 сходится
сходится
в круге 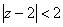
в круге 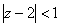
во всей плоскости 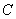 , кроме точек
, кроме точек 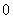 и
и 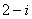
в круге 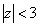
Если 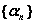 - бесконечно малая последовательность и
- бесконечно малая последовательность и 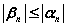 , при
, при 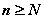
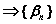 последовательность
последовательность
меньшего порядка малости
бесконечно большая
большего порядка малости
бесконечно малая
Четность тригонометрический функций sinx, cosx, tgx, ctgx следующая:
нечетная, четная, нечетная, нечетная
нечетная, четная, нечетная, четная
нечетная, четная, четная, нечетная
четная, нечетная, нечетная, нечетная
Функция 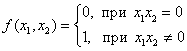 в точке (0, 0) имеет частные производные
в точке (0, 0) имеет частные производные 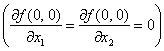 . Следовательно
. Следовательно
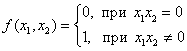 в точке (0, 0) имеет частные производные
в точке (0, 0) имеет частные производные 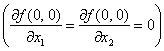 . Следовательно
. СледовательноФункция 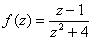
изолированных особых точек не имеет
имеет полюсы первого порядка в точках 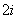 и
и 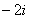
имеет полюсы второго порядка в точках 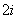 и
и 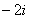
имеет полюс первого порядка в точке 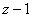
Если 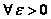
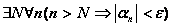 , то
, то 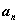
бесконечно большая
меньшего порядка малости 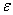
стремится к 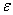
бесконечно малая
Число p изображается десятичной дробью
бесконечной непериодической
периодической
бесконечной
конечной
Многочлены Лежандра: Р0 = 1, Р1(х) = х, Р2 = 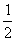 (3х2 - 1) Разложение элемента f(x) = -6x2 +x -5 по многочленам Лежандра имеет вид:
(3х2 - 1) Разложение элемента f(x) = -6x2 +x -5 по многочленам Лежандра имеет вид:
f(x) = -6P0 + 2P1 - 5P2
f(x) = -6P0 + P1 - 5P2
f(x) = -5P0 + P1 - 6P2
f(x) = -7P0 + P1 - 4P2
Написать уравнение касательной плоскости к поверхности шара х2 + у2 + z2 - 14 = 0 в точке Р(1,2,3).
х + 2у + 3z - 14 = 0
2х + 2у + 3z - 14 = 0
х + 2у + 2z - 14 = 0
х + 3у + 3z - 14 = 0
Если ряд 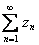 сходится, то
сходится, то
ряд 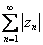 тоже сходится
тоже сходится
предел 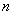 -го члена равен нулю:
-го члена равен нулю: 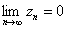
предел частичных сумм существует и равен нулю
ряд 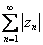 расходится
расходится
Взаимно однозначное соответствие между точками числовой оси и действительными числами означает, что
положительные и отрицательные целые числа являются координатами точек оси
все действительные числа лежат на оси
каждая точка оси изображается действительным числом - своей координатой и каждое действительное число оказывается координатой определенной точки
все рациональные числа изображаются точками оси
Сумма S всех членов бесконечно убывающей геометрической прогрессии, первый член которой равен b1, а знаменатель равен q, вычисляется по формуле
S = b1 · q
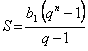
Объем тела, образованного вращением вокруг оси Ox фигуры, ограниченной параболой 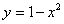 и осью Ox, вычисляется с помощью интеграла
и осью Ox, вычисляется с помощью интеграла

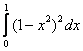
Решением уравнения Uxx + Uyy = 0 является функция
U = x + y2
U = x2y
U = x2 + y2
U = x2 - y2
Кривизна К кривой 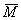 (t) = (acost, bsint, ct) вычисляется по формуле: К =
(t) = (acost, bsint, ct) вычисляется по формуле: К = 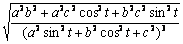 . Тогда кривизна кривой
. Тогда кривизна кривой 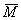 (t) = (5cost, 5sint, 5t) равна
(t) = (5cost, 5sint, 5t) равна
К = 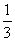
К = 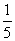
К = 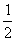
К = 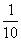
Даны два утверждения: 1) уравнение xUху - xyUz + xyz = 0 линейное неоднородное, 2) уравнение x2Ux - y2Uу + U2 = 0 линейное однородное. Утверждения
оба верны
первое неверно, второе верно
оба неверны
первое верно, второе неверно
для "ε > 0 $N > 0 такое, что при x > N выполняется неравенство |f(x) - ∞| < ε
при "M > 0 будет f(x) > M
для любого M > 0 найдется N > 0 такое, что при x > N выполняется неравенство |f(x)| > M; иначе говоря 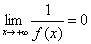
значения f(x) очень велики
Фундаментальным решением уравнения Лапласа на плоскости называется функция
u0 = ln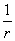 ;
;
u0 = r ;
u0 = 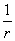 ;
;
u0 = 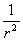 ;
;
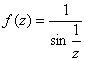 являются точки
являются точки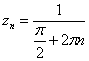
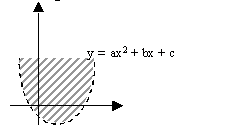
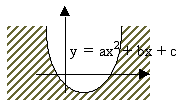

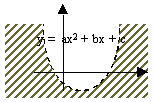
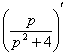 является
является