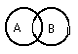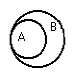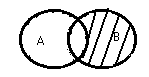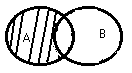Математический анализ (курс 2)
Теорема существования и единственности решения задачи Коши для дифференциального уравнения 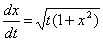 выполняется в области
выполняется в области
{-∞
{t>0, x>0}
{t>0, -∞
{t<0, x<0}
Число 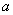 есть предел функции
есть предел функции 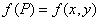 в точке
в точке 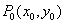 , если
, если
выполняется условие 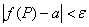
значения функции 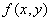 находятся в
находятся в 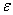 -окрестности
-окрестности 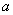
для 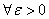 найдется
найдется 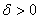 такое, что в любой точке
такое, что в любой точке 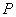 , принадлежащей области определения функции и попадающей в
, принадлежащей области определения функции и попадающей в 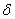 -окрестность
-окрестность 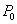 (кроме, быть может, самой точки
(кроме, быть может, самой точки 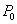 ) выполняется неравенство
) выполняется неравенство 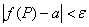 . Запись
. Запись 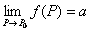
Точка 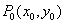 является точкой максимума функции
является точкой максимума функции 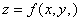 , если
, если
найдется такая 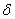 -окрестность
-окрестность 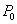 , что значение
, что значение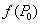 больше любого значения
больше любого значения 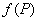 , принятого в этой окрестности
, принятого в этой окрестности
найдется такой интервал, содержащий 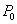 , что значение
, что значение 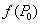 больше любого значения
больше любого значения 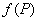 , принятого в этом интервале
, принятого в этом интервале
значение 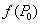 больше всех значений функции
больше всех значений функции 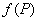
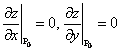
Даны функции: sinx, cosx, x2, x3. Из них четными являются
3
2
2, 4
2, 3
равен 2
не существует
равен 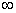 потому, что числитель при больших
потому, что числитель при больших 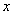 намного больше знаменателя
намного больше знаменателя
равен 1
_______ является дифференциальное уравнение 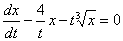
Однородным уравнением первого порядка
Уравнением с разделяющимися переменными
Уравнением с полным дифференциалом
Уравнением Бернулли
_____ является дифференциальное уравнение 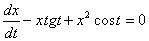
Уравнением с разделяющимися переменными
Однородным уравнением первого порядка
Уравнением с полным дифференциалом
Уравнением Бернулли
Производная 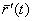 векторной функции
векторной функции 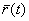 при
при 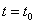 направлена по
направлена по
нормали к линии
касательной прямой к годографу функции 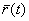 , проведенной в точке
, проведенной в точке 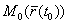
касательной прямой
касательной прямой в точке 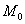
Ряд Фурье функции f(x) = |х| (-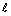 < x <
< x <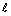 ), Т = 2ℓ, в точке х0 = ℓ сходится к значению
), Т = 2ℓ, в точке х0 = ℓ сходится к значению
расходится в точке х0 = 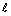
0
ℓ
1
Заданы функции:1) y = x2, 2) y = 2x + 1, 3) y = sinx, 4) y = ex. Взаимно однозначное соответствие между областью определения и областью значений задают функции с номерами
2, 4
3
2
1, 3
_______ является дифференциальное уравнение 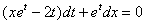
Уравнением с разделяющимися переменными
Уравнением с полным дифференциалом
Уравнением Бернулли
Однородным уравнением первого порядка
Дано множество: A = {x: |x| ³ 1, x ¹ 2}. Этому множеству соотвествует чертеж
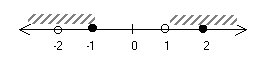
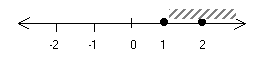
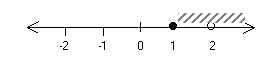
Площадь области, ограниченной линиями 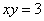 и
и 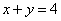 , вычисляется с помощью определенного интеграла
, вычисляется с помощью определенного интеграла
Функция 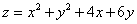 имеет в точке
имеет в точке
(-2, -3) - максимум
(-2, -3) - минимум
(2, 3) - стационарную точку
(2, 3) - максимум
Коэффициенты 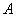 и
и 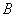 в формуле для полного приращения дифференцируемой в точке
в формуле для полного приращения дифференцируемой в точке 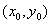 функции
функции 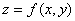 равны
равны
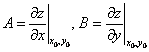
произвольным числам
График функции 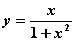
имеет асимптоту: 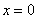
асимптот (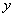 ) не имеет, так как знаменатель не обращается в нуль
) не имеет, так как знаменатель не обращается в нуль
не имеет точек разрыва и асимптот
имеет единственную асимптоту: 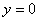
_______ является дифференциальное уравнение 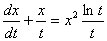
Однородным уравнением первого порядка
Уравнением с полным дифференциалом
Уравнением Бернулли
Уравнением с разделяющимися переменными
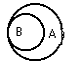
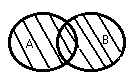
Множество А заданное графически это:
это:
[a; +¥)
(a; +¥)
(a; b) È (b; +¥)
[a; b] È (b; +¥)
Крыша может быть выпуклой (вниз) или вогнутой (выпуклой вверх). При дожде влага скапливается на ... крыше, при этом 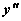 имеет знак ... (
имеет знак ... (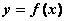 - уравнение крыши)
- уравнение крыши)
вогнутой и 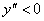 (знак -)
(знак -)
выпуклой и 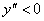 (знак -)
(знак -)
выпуклой и 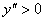 (знак +)
(знак +)
вогнутой и 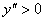 (знак +)
(знак +)
Ряд 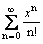 есть разложение функции
есть разложение функции
ех только на интервале (-1,1)
ln (1 + x) на промежутке -1 < x £ 1
ех на всей числовой прямой
sin x на всей числовой прямой
Дифференциальное уравнение (tx2 + sin t) dt + (t2 x + cosx) dx= 0 является
уравнением с полным дифференциалом
уравнением Бернулли
однородным уравнением первого порядка
уравнением с разделяющимися переменными
Геометрический ряд а + aq + aq2 + … сходится, если его знаменатель q
удовлетворяет неравенству |q| >1
равен 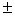 1
1
удовлетворяет неравенству q >1
удовлетворяет неравенству |q| <1
Кривизной 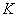 кривой линии в ее точке
кривой линии в ее точке 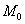 называется
называется
предел угла между касательными при 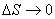
предел абсолютной величины угла между касательными при 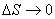
предел средней кривизны 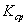 , когда
, когда 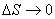 :
: 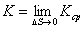
угол между касательными в точке 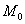
Положение точки 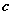 , о которой говорится в теоремах Лагранжа, Ролля, Коши, находится
, о которой говорится в теоремах Лагранжа, Ролля, Коши, находится
где-то между 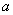 и
и 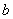 :
: 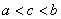
в одном из концов интервала
в точке 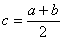
на середине отрезка 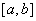
Ряд 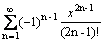 есть разложение в ряд Маклорена функции
есть разложение в ряд Маклорена функции
ln (1 + х)
sin x
ех
cos x
У графика функции 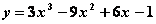
критических точек для 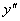 нет
нет
точка перегиба есть - это 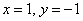
функция возрастает
точки перегиба нет
Предложение «Вам нравится сдавать тест?» ___________
является высказыванием, истинным
является неопределенным высказыванием
не является высказыванием
является высказыванием, ложным
Функция y = logа(х + 1) обращается в 0 в точке:
х = 0
х = 2
х = 1
х = -1
Бинормаль к кривой в некоторой точке - это
прямая в нормальной плоскости
плоскость, перпендикулярная касательной прямой
прямая, перпендикулярная к касательной и к главной нормали
другая нормаль
Множеством истинности для высказывания |x| < 1 является
(- ¥, 1)
(-1, 1)
[-1, 1]
(-¥, -1)
Некто вложил в банк деньги под 50% годовых. Через два года его вклад
увеличился меньше чем в 2 раза
увеличился в 2 раза
увеличился в 1,5 раза
увеличился более чем в 2 раза
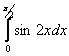 равен
равен равен
равен