Математический анализ (курс 2)
Высказывание 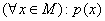 можно прочитать
можно прочитать
не для всякого х из М верно р(х)
существует х из М такое, что р(х)
всякий элемент х множества М обладает свойством р(х)
не существует такого х из М, что р(х)
_______ является дифференциальное уравнение 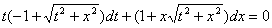
Уравнением с полным дифференциалом
Уравнением с разделяющимися переменными
Уравнением Бернулли
Однородным уравнением первого порядка
Дифференциальное уравнение 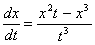 является
является
уравнением с полным дифференциалом
уравнением с разделяющимися переменными
уравнением Бернулли
однородным уравнением первого порядка
Ряды 1 + 1 + 1 + … + 1 + … и 1+ 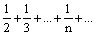
первый - сходится, второй - расходится
оба сходятся
первый - расходится, второй - сходится
оба расходятся
функция от 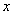
производная сложной функции
сложная функция от 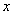 ; функция от функции; суперпозиция функций
; функция от функции; суперпозиция функций 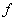 и
и 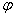
промежуточный аргумент
Объем тела, образованного вращением вокруг оси 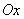 фигуры, ограниченной параболой
фигуры, ограниченной параболой 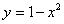 и осью
и осью 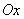 , вычисляется с помощью интеграла
, вычисляется с помощью интеграла
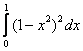

Геометрические ряды 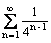 и
и 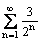
первый - сходится, второй - расходится
оба сходятся
оба расходятся
первый - расходится, второй - сходится
Торговец закупил на все свои деньги на оптовой базе товар и продал его с наценкой 20%. После распродажи он решил повторить столь удачную операцию. Всего он получил прибыли
42%
40%
44%
41%
Даны функции: sinx, cosx, x2, x3. Из них нечетными являются
1
2,3
4
1, 4
Ряд 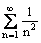
расходится, так как общий член стремится к нулю
расходится в силу интегрального признака сходимости
сходится в силу интегрального признака сходимости
расходится, так как общий член не стремится к нулю
A = {x: 2 £ x < 4, x ¹3}. Данное множество выражается как:
[2; 3) È (3;4)
[2; 3] È [3;4]
(2; 3) È (3;4)
[2; 3] È [3;4)
Ряд Фурье функции f(x) = |х| (-2 < x < 2), Т = 4, в точке х0 = 0 сходится к значению
2
1
расходится в точке х0 = 0
0
Ряд 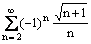
расходится
сходится условно
расходится абсолютно
сходится абсолютно
Теорема существования и единственности решения задачи Коши для дифференциального уравнения 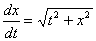 выполнена в области
выполнена в области
{t > -1, -¥ < x < +¥}
{t2 + x2 > 0}
{-¥ < t, x < +¥}
{x > -1, -¥ < t < +¥}
Разложение в ряд Маклорена функции у = cos 4x и область сходимости полученного ряда следующие:
1 + 2x + 4x2 + 6x3 + …(-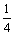 < x <
< x < 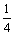 )
)
1 + х + х2 + х3 + … (-1 < x < 1)
Дифференциальное уравнение 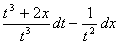 = 0 является
= 0 является
уравнением Бернулли
однородным уравнением первого порядка
уравнением с разделяющимися переменными
уравнением с полным дифференциалом
Ряд Маклорена функции у = cos 3x сходится
на всей числовой оси
только на интервале (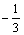 < x <
< x < 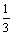 )
)
только на (-1,1)
только при х = 0
Длина дуги кривой 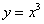 с концами в точках О(0, 0) и А(3, 27) вычисляется с помощью интеграла
с концами в точках О(0, 0) и А(3, 27) вычисляется с помощью интеграла
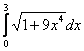
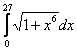
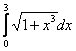
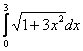
Площадь области, ограниченной линиями 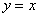 и
и 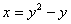 , вычисляется с помощью определенного интеграла
, вычисляется с помощью определенного интеграла
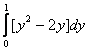
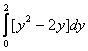
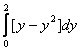
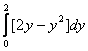
Числовой ряд называется сходящимся, если
предел общего члена ряда равен нулю
существует предел общего члена ряда
существует конечный предел n-й частичной суммы
предел частичной суммы ряда равен бесконечности
Необходимым условием существования экстремума функции 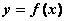 в точке
в точке 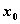 является условие
является условие
________является число 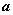 называется пределом последовательности
называется пределом последовательности 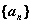 (
(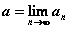 )
)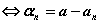
Бесконечно большой
Ограниченной
Бесконечно малой
Предложение «в городе N обитало не меньше 1000 жителей» является
сложным высказыванием
простым высказыванием
не является высказыванием
неопределенным высказыванием
Для дифференциального уравнения 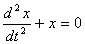 характеристическое уравнение имеет вид
характеристическое уравнение имеет вид
l2 + l + 1= 0
l2 + 1 = 0
l2 + l = 0
l2 - 1 = 0
Числовая ось - это прямая, на которой
выбрано начало отсчета
установлено направление
отсчитываются длины
выбрано начало отсчета, установлены направление и единица измерения длин
Частное решение дифференциального уравнения 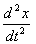 + 9x= cos 3t имеет вид:
+ 9x= cos 3t имеет вид:
c1 sin 3t + c2 cos 3t
c1t cos 3t
c1 cos 3t
(c1 sin 3t + c2 cos 3t) t
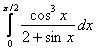 заменой переменной
заменой переменной 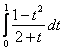
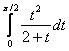
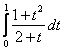

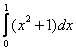 равен
равен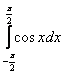 равен
равен