Математический анализ (курс 2)
{x: -1 £ х £ 1}, B = {y: 0 £ y £ 1}. Соответствие, заданное формулой : y = x2 является взаимно однозначным при
х Î [0,1]
х Î (-1,1)
х Î [-1,1]
х Î (0,1)
________является последовательность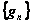 
, при 
, при Неограниченной
Бесконечно большой
Ограниченной
Бесконечно малой
, 
- две б.м. при 
. Тогда ониодного порядка
- высшего порядкаэквивалентны
не сравнимы
Ряд Фурье функции f(x) = х2 (-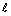
< x <), Т = 2 в точке х0 = 0 сходится к значению
< x <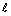), Т = 2 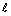в точке х0 = 0 сходится к значениюрасходится в точке х0 = 0
20
Первый член арифметической прогрессии равен двум, десятый - десяти. Сумма первых десяти членов этой прогрессии равна
65
55
50
60
Дифференциальное уравнение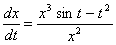 
является
являетсяуравнением с разделяющимися переменными
уравнением с полным дифференциалом
уравнением Бернулли
однородным уравнением первого порядка
Дана геометрическая прогрессия 1, 2, 4, … . Сумма её первых пяти членов равна
63
31
15
127
Ряд Фурье функции f(x) = |х| (-1 < x < 1), Т = 2 в точке х0 = -1 сходится к значению
расходится в точке х0 = -1
-1
1
0
Сумма S всех членов бесконечно убывающей геометрической прогрессии, первый член которой равен b1, а знаменатель равен q, вычисляется по формуле
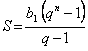
S = b1 · q
Функция y = sinx обладает следующими свойствами:
область определения [-1, 1], область значений (-¥, +¥), нечетная, нули хn = πn, (n - любое число)
область определения (-¥, +¥), область значений (-1, 1), нечетная, нули хn = πn, (n - любое число)
область определения (-¥, +¥), область значений [-1, 1], четная, нули хn = πn, (n - любое число)
область определения (-¥, +¥), область значений [-1, 1], нечетная, нули хn = πn, (n - любое число)
Ряд Фурье функции f(x) = х2 (-1< x < 1), Т = 2 в точке х0 =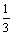 
сходится к значению
сходится к значению
расходится в точке х0 =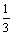
1
Любое действительное число может быть записано как десятичная дробь
конечная и периодическая
конечная или бесконечная (периодическая или непериодическая)
конечная
периодическая
Площадь области, ограниченной линиями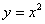 
и 
, вычисляется с помощью определенного интеграла
и 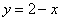, вычисляется с помощью определенного интеграла
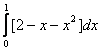
________ является дифференциальное уравнение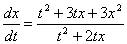 
Уравнением с полным дифференциалом
Уравнением с разделяющимися переменными
Уравнением Бернулли
Однородным уравнением первого порядка