Аналитическая геометрия и линейная алгебра
Уравнение 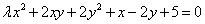 определяет кривую эллиптического типа при
определяет кривую эллиптического типа при 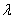
при всех 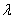
ни при каком 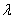
Уравнение 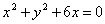 на плоскости ХОУ определяет
на плоскости ХОУ определяет
окружность с центром С (-3, 0)
эллипс с центром С (3, 0)
гиперболу с центром С (-3, 0)
гиперболу с центром С (3, 0)
На плоскости прямая у = 2х - 7 проходит через
точку (10, 13)
начало координат
точку (-1, 0)
точку (1, 1)
Через точку (0, 2, 1) проходит
прямая 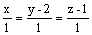
прямая 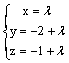
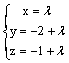
плоскость 2y + z = 0
плоскость 4(y + 2) + 5(z + 1) = 0
В параллелограмме 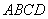 стороны
стороны 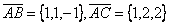 . Проекция
. Проекция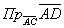 диагонали
диагонали 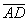 на сторону
на сторону 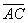 равна
равна
10
0
1
Уравнение прямой, проходящей через точку (1, 1) и перпендикулярной оси ОУ, имеет вид
у-1 = 0
х = у
х+у = 0
х-1 = 0
Центр симметрии гиперболы находится в начале координат. Действительная полуось b = 1, мнимая а = 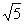 . Уравнение гиперболы имеет вид
. Уравнение гиперболы имеет вид
Квадратичная форма 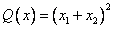 является
является
неположительно определенной
положительно определенной
знаконеопределенной
неотрицательно определенной
Данная поверхность 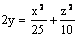 является
является
эллиптическим параболоидом
эллиптическим цилиндром
гиперболическим параболоидом
конусом
Прямые 4х+λу+1 = 0 и λх+у+4 = 0 параллельны, если число λ равно
-1
4
1
Площадь параллелограмма, построенного на векторах 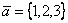 и
и 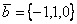 , равна
, равна
9 кв.ед.
27 кв.ед
1 кв.ед.
Координаты вершин параллелограмма 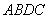 равны А (1,0,1), В (2,1,0), С (2,2,3). Проекция
равны А (1,0,1), В (2,1,0), С (2,2,3). Проекция 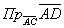 диагонали
диагонали 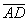 на сторону
на сторону 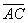 равна
равна
1
0
10
На плоскости прямая 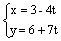
имеет направляющий вектор 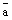 = (-4, 7)
= (-4, 7)
имеет направляющий вектор 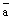 = (3, 6)
= (3, 6)
параллельна оси Оу
параллельна оси Ох
Уравнением y2 = 0 задается вырожденная поверхность второго порядка, представляющая собой
координатную плоскость Oxz
пустое множество
координатную плоскость Oyz
точку
Данная поверхность 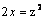 является
является
эллиптическим параболоидом
параболическим цилиндром
гиперболическим цилиндром
гиперболическим параболоидом
Координаты многочлена 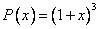 по базису
по базису 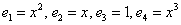 равны
равны
(1, 3, 1, 3)
(3, 3, 1, 1)
(1, 3, 3,1)
(3, 1, 3, 1)
Квадратичная форма 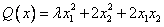 положительно определена при
положительно определена при 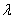
ни при каких 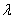
На плоскости прямую, проходящую через точку (-1, 1) и имеющую направляющий вектор 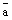 = (-3, 2), можно задать уравнением
= (-3, 2), можно задать уравнением
3(х + 1) - 2(у - 1) = 0
у = 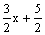
Тригонометрическая форма числа 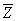 , комплексно сопряженного к
, комплексно сопряженного к 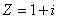 , имеет вид
, имеет вид
Гиперболоид 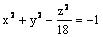 является
является
линейчатой поверхностью
поверхностью вращения вокруг оси Oz
поверхностью вращения вокруг оси Oy
поверхностью вращения вокруг оси Ox
Размерность пространства решений V системы уравнений 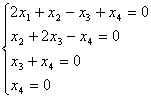
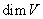 равна
равна
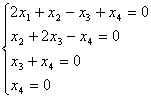
Две системы линейных уравнений эквивалентны, если
множества их решений совпадают
их матрицы совпадают
системы имеют одинаковое число переменных
системы имеют одинаковое число переменных и уравнений
Уравнением первой степени относительно x, y, z называется уравнение вида
F(x, y, z) = 0
Ax + By + Cz + D = 0
Ax + By + Cz + D = 0, A2 + B2 + C2 ¹ 0
Ax + By + Cz + D = 0, D ¹ 0
Прямые 4х+2у+5 = 0 и λх+у-1 = 0 перпендикулярны, если число λ равно
-1
-2
0
В пространстве многочленов степени 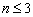 задан оператор дифференцирования
задан оператор дифференцирования 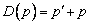 и функция
и функция 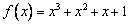 . Координаты образа
. Координаты образа 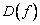 по базису
по базису 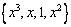 равны
равны
(2, 3, 4, 1)
(1, 2, 3, 4)
(1, 3, 2, 4)
(3, 2, 1, 1)
Из перечисленных прямых: 1) у-х = 1; 2) 3у = 5+3х; 3) 3у+3х+1=0; 4) х-2у-2=0 перпендикулярными к прямой у+х = 2 являются
1, 2
1, 3
только 3
2, 4
Даны два вектора 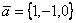 и
и 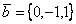 . Острый угол
. Острый угол 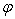 между этими векторами равен
между этими векторами равен
30°
0°
45°
60°
Даны векторы 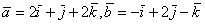 . Вектору
. Вектору 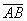 , где точки А (1,0,2) и В (2,1,3) ортогональны векторы
, где точки А (1,0,2) и В (2,1,3) ортогональны векторы
ни один из векторов
Собственный вектор 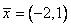 матрицы
матрицы 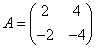 отвечает собственному значению
отвечает собственному значению
Данная поверхность 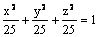 является
является
эллипсоидом
эллиптическим цилиндром
конусом
сферой
Из перечисленных прямых: 1) 2у = х-2; 2) у = 2х+1; 3) у+2х-1=0; 4) 2х+2у-3=0; 5) 4х-2у+3 = 0 перпендикулярными к прямой 2у+х-2 = 0 являются прямые
только 2
4
2, 5
1, 3
Решение системы 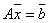 , где А - невырожденная матрица, можно получить по формуле
, где А - невырожденная матрица, можно получить по формуле
Каноническое уравнение прямой, проходящей через точку М0(1, 1) параллельно оси ОХ, имеет вид
х-1 = у-1
х+1 = у+1
Среди векторов 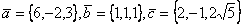 наибольшую длину имеет вектор
наибольшую длину имеет вектор
длины всех векторов равны
Уравнение прямой, проходящей через точки М(1, 2) и N(0, 3), имеет вид
х-у-3 = 0
х+у+3 = 0
у = -х+3
у = х+1
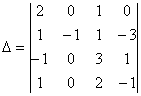 равен
равен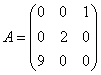 равны
равны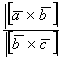 при
при 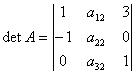 имеет вид
имеет вид