Дискретная математика
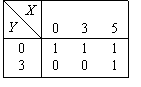
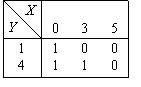
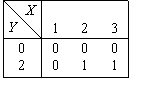
СДНФ булевой функции, задаваемой таблицей 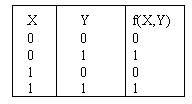 содержит элементарную конъюнкцию
содержит элементарную конъюнкцию
 содержит элементарную конъюнкцию
содержит элементарную конъюнкциюX Y
X 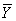
Из двух пар чисел (8, 13) и (13, 11) бинарное отношение R(a, b) = b < a выполняется
только для второй
для обеих
только для первой
ни для одной
Заданы множества 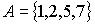 и
и 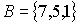 . Верным для них будет утверждение
. Верным для них будет утверждение
«Множества А и В не имеют общих элементов»
«Множества А и В равны»
«Множество А включает в себя множество В»
«Множество А есть подмножество множества В»
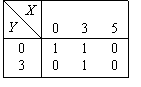
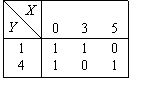
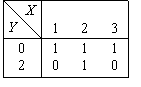
Булева функция, задаваемая таблицей 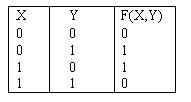 называется
называется
 называется
называетсяимпликацией
суммой по модулю 2
дизъюнкцией
эквивалентностью
Если отношение задано неравенством: 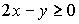 , то данному отношению принадлежит следующая пара чисел
, то данному отношению принадлежит следующая пара чисел
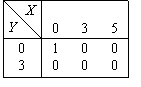
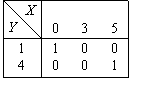
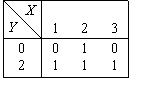
СДНФ булевой функции, задаваемой таблицей 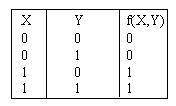 содержит элементарную конъюнкцию
содержит элементарную конъюнкцию
 содержит элементарную конъюнкцию
содержит элементарную конъюнкциюXY
X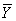
Предикатная формула 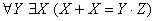 представляет собой
представляет собой
трехместный предикат P(X, Y, Z)
высказывание
одноместный предикат P(Z)
двуместный предикат P(X, Y)
Для функции f(X) = X2 /(3Х-1) суперпозиция f(2-X) равна
Х2 / (3Х –1)
X2 / (4-3X)
(2-Х)2 / (3Х –1)
(2-X)2 / (4-3X)
Если отношение задано неравенством: 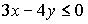 , то данному отношению принадлежит следующая пара чисел
, то данному отношению принадлежит следующая пара чисел
Числовое множество 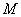 задается порождающей процедурой: (1)
задается порождающей процедурой: (1) 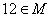 ; (2) если
; (2) если 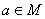 , то
, то 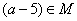 ; (3) если
; (3) если 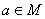 , то
, то 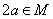 . Элемент
. Элемент 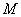 , определяемый последовательностью операций (2) → (3) → (2) → (3), равен ____ (ответ – целое число).
, определяемый последовательностью операций (2) → (3) → (2) → (3), равен ____ (ответ – целое число).
На факультете учатся студенты, обучающиеся платно, и студенты, обучающиеся бесплатно. Пусть А – множество всех студентов факультета; В – множество студентов факультета, обучающихся платно. Тогда пересечением 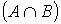 этих множеств будет
этих множеств будет
множество студентов факультета, обучающихся платно
множество всех студентов факультета
пустое множество
множество студентов факультета, обучающихся бесплатно
Предикат (X > 1) & (X < 2) задает множество действительных чисел
-¥ < X < +¥
X Î [1, 2]
X Î (1, 2)
X Ï [1, 2]
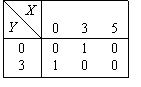
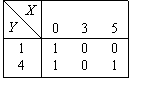
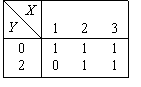
Функция, заданная на двумерном единичном кубе 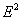 ,
, 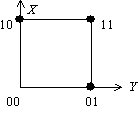 может быть представлена формулой
может быть представлена формулой
 может быть представлена формулой
может быть представлена формулойХÚY
Пусть A и B - множества, изображенные на рисунке: 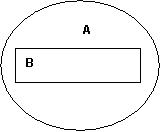 Тогда объединением этих множеств является
Тогда объединением этих множеств является
 Тогда объединением этих множеств является
Тогда объединением этих множеств являетсяА\В
В
А
Функция, заданная на двумерном единичном кубе 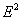 ,
, 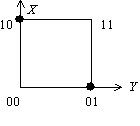 может быть представлена формулой
может быть представлена формулой
 может быть представлена формулой
может быть представлена формулойДаны два высказывания: A – «треугольник равносторонний»; B – «все стороны треугольника равны». Тогда на языке алгебры логики предложение: «Если в треугольнике все стороны равны, то он не равносторонний» имеет вид …
Заданы множества 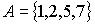 и
и 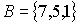 . Верным для них будет утверждение
. Верным для них будет утверждение
«Множества А и В не имеют общих элементов»
«Множество А есть подмножество множества В»
«Множества А и В равны»
«Множество А включает в себя множество В»
Если отношение задано неравенством: 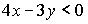 , то данному отношению принадлежит следующая пара чисел
, то данному отношению принадлежит следующая пара чисел
Дано множество элементов вида 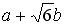 , где a, b –действительные числа, с операцией «
, где a, b –действительные числа, с операцией « » (умножение) и нейтральным элементом 1 (единица). Элемент, симметричный элементу
» (умножение) и нейтральным элементом 1 (единица). Элемент, симметричный элементу 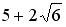 , равен…
, равен…
нет симметричного
Двоичная запись десятичного числа 24 содержит ____ двоичных знаков (ответ – целое число)
Предикатная формула 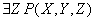 представляет собой
представляет собой
одноместный предикат 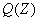
двуместный предикат 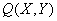
истинное высказывание
ложное высказывание
Булевы функции 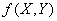 и
и 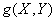 задаются столбцами значений
задаются столбцами значений 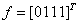 и
и 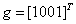 . Столбцом значений функции
. Столбцом значений функции 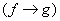 является
является
Булевы функции 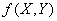 и
и 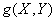 задаются столбцами значений
задаются столбцами значений 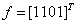 и
и 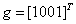 . Столбцом значений функции
. Столбцом значений функции 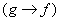 является
является
Число 151 в двоичной системе счисления имеет вид
10010011
10010101
10010110
10010111
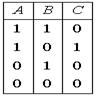
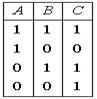
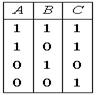
Операции над высказываниями А и В (дизъюнкция, конъюнкция и отрицание) задаются с помощью таблицы истинности 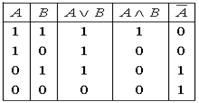 . Тогда, таблицей истинности для сложного высказывания
. Тогда, таблицей истинности для сложного высказывания 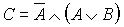 будет таблица
будет таблица
 . Тогда, таблицей истинности для сложного высказывания
. Тогда, таблицей истинности для сложного высказывания 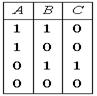
Бинарное отношение P: X < Y на множестве действительных чисел является
антисимметричным
нетранзитивным
транзитивным
симметричным
Предикатная формула $X,Y (X + Y = Z – X) представляет собой
одноместный предикат P(Z)
высказывание
трехместный предикат P(X, Y, Z)
двуместный предикат P(X, Y)
Предикат (X > 1) Ú (X < 2) задает множество действительных чисел
X Ï [1, 2]
-¥ < X < +¥
(X ≤ 1) & (X ≥ 2)
X Î [1, 2]
Множество слов русского языка с алфавитным упорядочением является
линейно упорядоченным
неупорядоченным
неопределенным
частично упорядоченным
На факультете учатся студенты, имеющие домашний персональный компьютер, и студенты, не имеющие домашнего персонального компьютера. Пусть А – множество всех студентов факультета; В – множество студентов факультета, имеющих домашний персональный компьютер. Тогда объединением 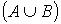 этих множеств будет
этих множеств будет
множество студентов факультета, не имеющих домашнего персонального компьютера
множество студентов факультета, имеющих домашний персональный компьютер
пустое множество
множество всех студентов факультета
Булевы функции 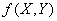 и
и 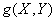 задаются столбцами значений
задаются столбцами значений 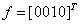 и
и 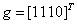 . Столбцом значений функции
. Столбцом значений функции 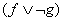 является [ _ ]T.
является [ _ ]T.
Заданы множества 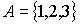 и
и 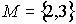 . Верным для них будет утверждение
. Верным для них будет утверждение
«Множество М включает в себя множество А»
«Множества A и M равны»
«Множество A есть подмножество множества M»
«Множество M есть подмножество множества A»
На факультете учатся студенты, принимающие участие в художественной самодеятельности, и студенты, не принимающие участие в художественной самодеятельности. Пусть А – множество всех студентов факультета; В – множество студентов факультета, принимающих участие в художественной самодеятельности. Тогда объединением 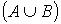 этих множеств будет
этих множеств будет
множество студентов факультета, не принимающих участия в художественной самодеятельности
множество всех студентов факультета
множество студентов факультета, принимающих участие в художественной самодеятельности
пустое множество
Сопоставьте наборы булевых переменных функций трех переменных и соответствующие элементарные конъюнкции:
110
X  Z
Z
011
101
X Y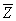
Если в частично упорядоченном множестве М есть наименьший элемент, то в нем
есть ровно один минимальный
нет ни одного максимального элемента
есть наибольший элемент
есть хотя бы два различных минимальных элемента
Бинарное отношение 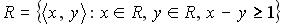 обладает свойствами …
обладает свойствами …
антирефлексивности и антисимметричности
рефлексивности и симметричности
антирефлексивности и транзитивности +
антисимметричности и транзитивности +
Схема из функциональных элементов реализует функцию 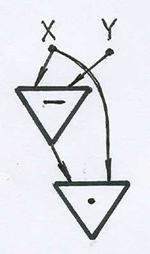

(X-Y) • Y
(X-Y) • X
(Y- X) • X
(Y-X) • Y
Свойством симметричности обладает бинарное отношение ...
«быть подобным»
«быть делителем»
«быть моложе»
«быть выше ростом»
На координатной плоскости изображено декартово произведение А×В множеств (отрезков) А = [2, 6] и B = [1, 4]. 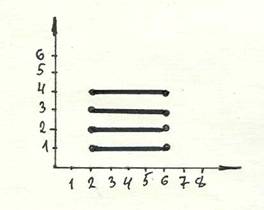

A и В – множества действительных чисел
А - множество действительных чисел, В - множество целых чисел
А и B – множества целых чисел
A - множество целых чисел, В - множество действительных чисел
Из двух пар чисел (8, 14) и (14, 14) бинарное отношение R(a, b) = b > a выполняется
ни для одной
для обеих
только для первой
только для второй
Тождество ¬(X & Y) = ¬X Ú ¬Y называется законом
тождества
де Моргана
Поста
Буля
 , где
, где