Основы математического анализа
Поверхность уровня функции u = x2 + y2 + z2 в точке M0(1,1,1) имеет уравнение
x2 + y2 + z2 = 3
x2 + y2 + z2 = 1
x2 + y2 + z2 = 0
2x + 2y + 2z = 6
Какие утверждения верны? a) общее решение дифференциального уравнения у¢ - у = 0 имеет вид: Cех b) общее решение дифференциального уравнения у¢ + у = 0 имеет вид: Cе-x c) общее решение дифференциального уравнения у¢ - у = 0 имеет вид: Cxех d) общее решение дифференциального уравнения у¢ + у = 0 имеет вид: Cxе-x
d
c
b
a
Область определения функции 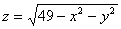 есть множество
есть множество
{(x, y): -7 < x < 7, -7 < y < 7}
{(x, y): x + y £ 7}
{(x, y): x2 + y2 £ 49 }
{(x, y): -¥ < x < ¥, 0 < y < 7}
Полный дифференциал функции z = x2 + y в точке P0(0,0) равен
2dx
2dx + dy
0
dy
Укажите соответствие между дифференциальными уравнениями и их общими решениями
y² - y¢ = 0
С1 + С2e-2x
y² + y¢ = 0
С1 + С2e-x
y² + 2y¢ = 0
С1 + С2ex
Характеристическое уравнение для разностного уравнения y(x + 2) – 4y(x + 1) + 4y(x) = 0 имеет вид
r2 – 4r = 0
r2 – 4r + 4 = 0
r2 + 4 = 0
r2 – 4r – 4 = 0
Какие утверждения верны? a) Задача Коши у² - 2у¢ + у = 0, у(0) = 1, у¢(0) = 0 имеет решение ex b) Задача Коши у² - 2у¢ + у = 0, у(0) = 1, у¢(0) = 0 имеет решение (1 – x)ex c) Задача Коши у² - 2у¢ + у = 0, у(0) = 0, у¢(0) = 1 имеет решение xex d) Задача Коши у² - 2у¢ + у = 0, у(0) = 0, у¢(0) = 1 имеет решение (1+x)ex
a
c
b
d
Область определения функции 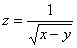 есть множество
есть множество
{(x, y): x – y ³ 0}
{(x, y): x ³ y}
{(x, y): y < x}
{(x, y) : x < y}
Общее решение дифференциального уравнения dy – 3x2dx = 0
y = x4
y = x2 + C
y = x3 + C
y = x + C
Частная производная 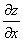 функции z = ln(x + y2) равна
функции z = ln(x + y2) равна
(x + y2) 2y
x + y2
(x + y2) x
Общее решение дифференциального уравнения 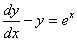
y = (x + C)ex
y = xex + C
y = exC
y = x + C
Укажите соответствие между дифференциальными уравнениями и их характеристическими уравнениями.
y² + y = 0
r2 – r = 0
y² + y¢ + y = 0
r2 + r + 1 = 0
y² - y¢ = 0
r2 + 1 = 0
Какие дифференциальные уравнения являются уравнениями с разделяющимися переменными? a) 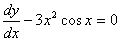 , b)
, b) 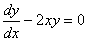 , c)
, c) 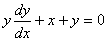 , d)
, d) 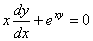
d
a
c
b
Какие утверждения верны? a) частное решение уравнения y(x+2) – 4y(x+1) + 4y(x) = 0, y(0) = 1, y(1) = 2 равно 2x b) частное решение уравнения y(x+2) – 4y(x+1) + 4y(x) = 0, y(0) = 1, y(1) = 2 равно x 2x c) частное решение уравнения y(x+2) – 6y(x+1) + 9y(x) = 0, y(0) = 1, y(1) = 3 равно 3x d) частное решение уравнения y(x+2) – 6y(x+1) + 9y(x) = 0, y(0) = 1, y(1) = 3 равно x3x
d
a
c
b
Укажите соответствие между дифференциальными уравнениями и корнями их характеристических уравнений.
y² + py¢ + q = sinx
r1 = r2 = 1
y² + 2y¢ + y = 1
r1 = r2 = -1
y² - 2y¢ + y = 0
Укажите соответствие между дифференциальными уравнениями и их частными решениями
y² - 2y¢ + y = 2sinx
-x
y² - 2y¢ + y = 5x + 1
5x + 11
y² - 2y¢ + y = -x + 2
cosx
Линия уровня функции z = x2 – y2 в точке P0(1,0) имеет уравнение
2x - 2y = 1
x2 – y2 = 1
x2 – y2 = 0
x2 – y2 = const
Частное решение дифференциального уравнения y² - 2y¢ + y = 0, удовлетворяющее начальным условиям y(0) = 1, y¢(0) = 0, равно
(1 – x)ex
2ex
ex
2x
Решение задачи Коши для дифференциального уравнения y¢ - y = 0, y(0) = 2 равно
2cosx
2
2ex
2 + sinx
Общее решение дифференциального уравнения dy – cosxdx = 0
y = cosx + C
y = tgx
y = sinx + C
y = x + C
Общее решение дифференциального уравнения dy – sinxdx = 0
y = sinx
y = tgx
y = cosx + C
y = - cosx + C
Какие утверждения верны? a) корни характеристического уравнение для разностного уравнения y(x+2) – 4y(x+1) + 4y(x) = 0 равны r1 = r2 = 2 b) корни характеристического уравнение для разностного уравнения y(x+2) + 4y(x+1) + 4y(x) = 0 равны r1 = r2 = -2 c) корни характеристического уравнение для разностного уравнения y(x+2) – 4y(x+1) + 4y(x) = 0 равны r1 = r2 = 1 d) корни характеристического уравнение для разностного уравнения y(x+2) + 4y(x+1) + 4y(x) = 0 равны r1 = r2 = 2
с
d
a
b
Укажите соответствие между дифференциальными уравнениями и их характеристическими уравнениями.
y² - 2y¢ + 5y = 1
r2 = 0
y² + 2y¢ + 5y = 0
r2 + 2r + 5 = 0
y² = sinx
r2 - 2r + 5 = 0
Градиентом функции z = f(x, y) в точке P0(x0,y0) называется
число, равное 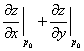
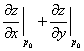
вектор, равный 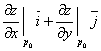
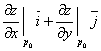
число, равное 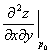
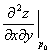
вектор, равный 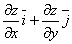
Укажите соответствие между дифференциальными уравнениями и их решениями.
Общее решение дифференциального уравнения y² + py¢ + qy = 0 (p,q – постоянные) в случае равных корней характеристического уравнения r1 = r2 = r имеет вид
C1erx
C2erx
(C1 + C2x)erx
C1erx + C2erx
Какие дифференциальные уравнения первого порядка являются уравнениями Бернулли ? a) 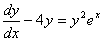 b)
b) 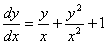 , c)
, c) 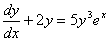 , d)
, d) 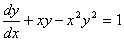
a
b
d
c
Полный дифференциал функции z = x3 + y3 в точке P0(-1,-1) равен
3(dx + dy)
-3dx - 3dy
3dx - 3dy
dx + dy
Область определения функции 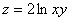 есть множество
есть множество
{(x, y) : xy > 0}
{(x, y) : x > 0, y > 0}
{(x, y) : xy > 1}
{(x, y) : x < 0, y < 0}
Какие утверждения верны? a) характеристическое уравнение для y² + y = 0 имеет корни 1; -1 b) характеристическое уравнение для y² + y = 0 имеет корни i; -i c) характеристическое уравнение для y² - y = 0 имеет корни 1; -1 d) характеристическое уравнение для y² - y = 0 имеет корни i; -i
b
d
a
c
Укажите соответствие между функциями и их частными производными
0
2x
2y
Какие утверждения верны? a) общее решение дифференциального уравнения y² + y = 0 имеет вид С1cosx + С2sinx b) общее решение дифференциального уравнения y² + y = 0 имеет вид С1ex + С2 e-x c) общее решение дифференциального уравнения y² - y = 0 имеет вид С1ex + С2 e-x d) общее решение дифференциального уравнения y² - y = 0 имеет вид С1cosx + С2sinx
a
b
d
c
Частное решение дифференциального уравнения y² - 2y¢ + y = 4e2x равно
4e2x
e-2x
sin2x
e2x
Какие утверждения верны? a) Задача Коши у² - 2у¢ + у = 0, у(0) = 0, у¢(0) = 2 имеет решение 2xex b) Задача Коши у² - 2у¢ + у = 0, у(0) = 0, у¢(0) = 2 имеет решение ex c) Задача Коши у² - 2у¢ + у = 0, у(0) = 0, у¢(0) = 1 имеет решение xex d) Задача Коши у² - 2у¢ + у = 0, у(0) = 0, у¢(0) = 1 имеет решение ex
a
c
d
b
Полный дифференциал функции z = x + y2 в точке P0(1,1) равен
dx + dy
dx + 2dy
2dx + dy
y2 dx + x dy
Полный дифференциал функции z = x4 – y4 в точке P0(1,1) равен
2dx + 2dy
2dx - 2dy
dx - dy
4dx - 4dy
Укажите соответствие между функциями f(x,y) и их векторами-градиентами в точке (1,0)
-x2 + y2
x2 + (y + 5)2
X2 – y2 + 5
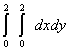 равен Напишите число
равен Напишите число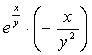
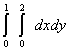 равен
равен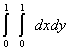 равен
равен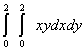 равен
равен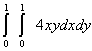 равен Напишите число
равен Напишите число