Элементы теории функций и функциональный анализ
Евклидово, или унитарное, линейное пространство, полное относительно нормы, согласованной со скалярным произведением, называется
гильбертовым
компактным
нормированным
банаховым
Точка х Î А называется предельной для подмножества В Í А, если любая e-окрестность точки х содержит точку множества В, отличную от точки х. Тогда множеством предельных точек множества (-1,+¥) является
[-1,+ ¥]
[-1,+ ¥)
(-1,+ ¥)
(-¥,-1]
Пусть  евклидово, или унитарное, пространство со скалярным произведением
евклидово, или унитарное, пространство со скалярным произведением 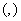 . Рассматривается некоторый оператор
. Рассматривается некоторый оператор 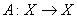 . Он самосопряженный, если: A)
. Он самосопряженный, если: A) 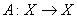 - линейный; B)
- линейный; B) 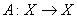 определен на всем
определен на всем  ; С)
; С) 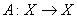 - ограничен; D) для любых
- ограничен; D) для любых 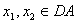
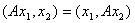 E) для любых
E) для любых 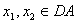
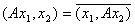 ;
;
все
одновременно A), B) и D)
только A) и D)
одновременно A), B) и C)
Найти норму функционала 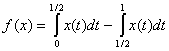 , определенного на пространстве
, определенного на пространстве 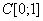 (укажите целое число)
(укажите целое число)
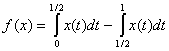 , определенного на пространстве
, определенного на пространстве Косинус угла между элементами f(x) и g(x) в пространстве L2 [a,b] определяется по формуле: cos(f(x),g(x)) = 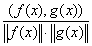 ; (f(x),g(x)) =
; (f(x),g(x)) = 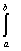 f(x)×g(x)dx ;
f(x)×g(x)dx ; 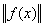 =
= 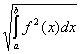 . Тогда косинус угла между элементами x4 и 1 в пространстве L2 [0,2] равен
. Тогда косинус угла между элементами x4 и 1 в пространстве L2 [0,2] равен
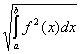 . Тогда косинус угла между элементами x4 и 1 в пространстве L2 [0,2] равен
. Тогда косинус угла между элементами x4 и 1 в пространстве L2 [0,2] равен-0,5
0,6
0,8
-0,1
Коэффициент ряда Фурье элемента f(x) = 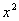 по ортогональной системе 1, coskx, sinkx, k = 1,2,… пространства
по ортогональной системе 1, coskx, sinkx, k = 1,2,… пространства 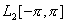 при сos2x равен ___ (укажите целое число)
при сos2x равен ___ (укажите целое число)
Полное линейное нормированное пространство называется
компактным
гильбертовым
евклидовым
банаховым
Многочлены Лежандра: Р0 = 1, Р1(х) = х, Р2 = 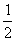 (3х2 - 1). Разложение элемента f(x) = 6x2 +4x +2 по многочленам Лежандра имеет вид:
(3х2 - 1). Разложение элемента f(x) = 6x2 +4x +2 по многочленам Лежандра имеет вид:
f(x) = 6P0 + 4P1 + 2P2
f(x) = 4P0 + 4P2
f(x) = 4P0 + 4P1 + 4P2
f(x) = 2P0 + 4P1 + 6P2
Выберите предложения, справедливые для гильбертова пространства:
вещественное пространство, снабженное скалярным произведением
евклидово пространство с фиксированным скалярным произведением
евклидово, или унитарное, линейное пространство, полное относительно нормы, согласованной со скалярным произведением
любое конечномерное евклидово или унитарное пространство
Пусть 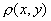 - метрика на множестве
- метрика на множестве  . Образуем некоторую новую функцию, которая может быть, а может и не быть метрикой. Если новая функция
. Образуем некоторую новую функцию, которая может быть, а может и не быть метрикой. Если новая функция 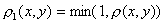 , то она ____________ метрикой (заполните пробел связкой)
, то она ____________ метрикой (заполните пробел связкой)
Укажите регулярные числа оператора А в евклидовом пространстве R2 A = 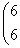
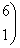 :
:
(-¥;-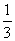 ) È (-
) È (-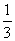 ; 0,1 ) È (0,1;+ ¥)
; 0,1 ) È (0,1;+ ¥)
(-¥,-3) È (-3,10) È (10,+ ¥)
(-¥;-0,1) È (-0,1; 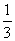 ) È (
) È (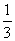 ;+ ¥)
;+ ¥)
(-¥,-10) È (-10,3) È (3,+ ¥)
Применение алгоритма ортогонализации Грама-Шмидта к системе векторов u {0,1,-1}, v {-2,2,4} евклидова пространства R3 дает векторы u,w, причем вектор w равен
{-2,3,3}
{-3,2,2}
{-2,2,3}
{-3,2,3}
В линейном пространстве многочленов, рассматриваемых на отрезке 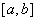 положим
положим 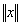 =
=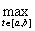
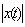 . Верно утверждение: это пространство
. Верно утверждение: это пространство
является нормированным, но не банаховым
нормировано и банахово
не нормировано, но банахово
не нормировано и не банахово
Все комплексные числа, за исключением регулярных, называются ________ линейного оператора (укажите определяемое понятие)
Уравнение х(t) - 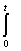 ln(t2s - s3)x(s)ds = et является интегральным уравнением Вольтера _______ (какого?) рода (укажите порядок словом рода)
ln(t2s - s3)x(s)ds = et является интегральным уравнением Вольтера _______ (какого?) рода (укажите порядок словом рода)
Пусть  топологическое пространство. Укажите верные утверждения:
топологическое пространство. Укажите верные утверждения:
объединение открытого множества и произвольного множества - замкнуто
объединение конечного числа замкнутых множеств - замкнуто
пересечение любого числа замкнутых множеств - замкнуто
если 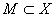 и
и 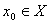 , то
, то 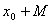 - открыто
- открыто