Элементы теории функций и функциональный анализ
Расстояние от f(x) до g(x) в пространстве С[a,b] определяется по формуле: r(f(x),g(x)) = 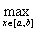
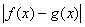 . Тогда расстояние между 2х3 + 2 и 3x2 + 12х в С[-1,3] равно
. Тогда расстояние между 2х3 + 2 и 3x2 + 12х в С[-1,3] равно
19
9
8
18
Норма оператора 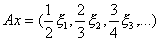 , действующего в
, действующего в 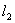 , равна _______ (укажите число)
, равна _______ (укажите число)
Уравнение 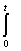 (2t2 - sins)x(s)ds = tgt является интегральным уравнением Вольтера _____ (какого?) рода (укажите порядок словом)
(2t2 - sins)x(s)ds = tgt является интегральным уравнением Вольтера _____ (какого?) рода (укажите порядок словом)
Наилучшее линейное приближение функции 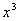 в пространстве
в пространстве 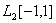 равно ____ (укажите ответ в виде алгебраического выражения)
равно ____ (укажите ответ в виде алгебраического выражения)
Уравнение x(t) -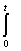 cos(t-s)x(s)ds = lnt является интегральным уравнением Вольтера ______ (какого?) рода (укажите порядок словом)
cos(t-s)x(s)ds = lnt является интегральным уравнением Вольтера ______ (какого?) рода (укажите порядок словом)
В линейном пространстве многочленов, рассматриваемых на отрезке 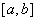 положим
положим 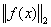 =
= 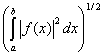 . Верно утверждение: а) это пространство нормировано; b) это пространство банахово
. Верно утверждение: а) это пространство нормировано; b) это пространство банахово
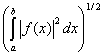 . Верно утверждение: а) это пространство нормировано; b) это пространство банахово
. Верно утверждение: а) это пространство нормировано; b) это пространство банаховоa
b
оба верны
оба неверны
Пусть 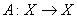 - вполне непрерывный линейный оператор в банаховом пространстве
- вполне непрерывный линейный оператор в банаховом пространстве  , причем
, причем 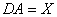 . Тогда: А) неоднородное уравнение
. Тогда: А) неоднородное уравнение 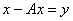 имеет единственное решение для любого
имеет единственное решение для любого 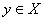 ; В) однородное уравнение
; В) однородное уравнение 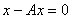 имеет ненулевое решение. Какие выводы возможны:
имеет ненулевое решение. Какие выводы возможны:
только В)
и А), и В)
только А)
либо А), либо В)
Если j(х) является отображением отрезка [a,b] в себя и имеет непрерывную производную j¢(х) на отрезке [a,b], то коэффициент сжатия оценивается по формуле q = 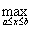 êj¢(х) ê. Тогда отображение j(х) = х2 отрезка [-0,4 ; 0,3] в себя является сжатым с коэффициентом сжатия _______ (укажите ответ в виде десятичной дроби)
êj¢(х) ê. Тогда отображение j(х) = х2 отрезка [-0,4 ; 0,3] в себя является сжатым с коэффициентом сжатия _______ (укажите ответ в виде десятичной дроби)
Известно, что расстояние от точки 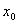 линейного нормированного пространства
линейного нормированного пространства  до гиперплоскости
до гиперплоскости 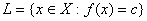 находится по формуле
находится по формуле 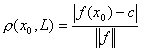 . Если
. Если 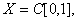
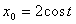 и
и 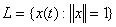 , то
, то 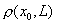 равно
равно
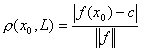 . Если
. Если 1
cos1
sin1
1/3
Рассматривается неоднородное уравнение Вольтерра второго рода в конечномерном пространстве 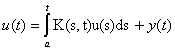 . Для его разрешимости достаточно доказать, что (укажите верное условие):
. Для его разрешимости достаточно доказать, что (укажите верное условие):
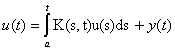 . Для его разрешимости достаточно доказать, что (укажите верное условие):
. Для его разрешимости достаточно доказать, что (укажите верное условие):соответствующее однородное уравнение имеет лишь нулевое решение
его решения есть решения соответствующего однородного уравнения
его единственное решение - нулевое
соответствующее однородное уравнение имеет более одного решения
Если j(х) является отображением отрезка [a,b] в себя и имеет непрерывную производную j¢(х) на отрезке [a,b], то коэффициент сжатия оценивается по формуле q = 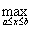 êj¢(х) ê . Тогда отображение j(х) = х2 отрезка [-0,4 ; 0,3] в себя является сжатым с коэффициентом сжатия
êj¢(х) ê . Тогда отображение j(х) = х2 отрезка [-0,4 ; 0,3] в себя является сжатым с коэффициентом сжатия
0,16
0,8
-0,8
0,6
Укажите спектр линейного оператора А в евклидовом пространстве R2 A=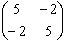 :
:
{- 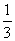 ;
; 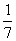 }
}
{-7;-3}
{3;7}
{ 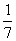 ;
; 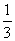 }
}
Если j(х) является отображением отрезка [a,b] в себя и имеет непрерывную производную j¢(х) на отрезке [a,b], то коэффициент сжатия оценивается по формуле q = 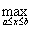 êj¢(х) ê. Тогда отображение j(х) = х3 отрезка [-0,5 ; 0,4] в себя является сжатым с коэффициентом сжатия
êj¢(х) ê. Тогда отображение j(х) = х3 отрезка [-0,5 ; 0,4] в себя является сжатым с коэффициентом сжатия
-0,75
0,48
0,5
0,75
Норма оператора 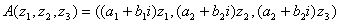 на унитарном пространстве С3 определяется по формуле
на унитарном пространстве С3 определяется по формуле 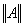 = max{
= max{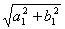 ,
,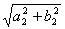 ,
,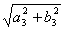 }. Тогда норма оператора
}. Тогда норма оператора 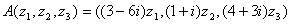 равна
равна
6
5
Для решения интегральных уравнений Фредгольма на практике применяют следующие способы:
сводят исходное уравнение к однородной системе однородной линейных уравнений
используют метод последовательных приближений
используют аппроксимацию ядра вырожденным ядром
сводят исходное уравнение к системе лпнейных уравнений
Норма элемента f(x) в пространстве С [a,b] определяется по формуле: 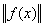 =
= 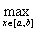
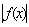 . Тогда норма элемента 2x3 - 9x2 + 12x + 1 в пространстве С[0,2] равна___________ (укажите целое число)
. Тогда норма элемента 2x3 - 9x2 + 12x + 1 в пространстве С[0,2] равна___________ (укажите целое число)
Расстоянием между множествами 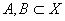 называется число
называется число 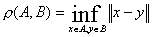 . Замыкание
. Замыкание 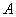 обозначается
обозначается 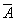 . Укажите верные равенства:
. Укажите верные равенства:
Рассматривается линейный оператор 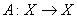 и его характеристические и собственные числа. Укажите верные утверждения:
и его характеристические и собственные числа. Укажите верные утверждения:
характеристическое число не может быть равно нулю
собственное значение может быть равно нулю
любое собственное число обратно некоторому характеристическому числу
характеристические числа суть числа, обратные к собственным значениям оператора A
Норма элемента f(x) в пространстве L2 [a,b] определяется по формуле: 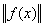 =
= 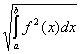 . Тогда норма элемента ex в пространстве L2 [ln2,ln6] равна
. Тогда норма элемента ex в пространстве L2 [ln2,ln6] равна
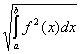 . Тогда норма элемента ex в пространстве L2 [ln2,ln6] равна
. Тогда норма элемента ex в пространстве L2 [ln2,ln6] равна16
6
4
18
Укажите возможные связки в теореме. Пусть оператор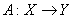 линейный. Тогда он непрерывен в
линейный. Тогда он непрерывен в  : A) тогда и только тогда, когда он ограничен; B) когда
: A) тогда и только тогда, когда он ограничен; B) когда  банахово пространство; С) если он непрерывен в точке
банахово пространство; С) если он непрерывен в точке 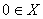 ; D) когда
; D) когда 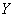 банахово пространство
банахово пространство
А) и С)
В) и D)
С) и D)
A)
Функция, сопоставляющая каждому элементу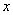 линейного пространства
линейного пространства  число
число 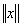 со следующими свойствами: a)
со следующими свойствами: a) 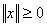 , причем
, причем 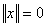
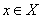 тогда и только тогда, когда
тогда и только тогда, когда 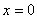 ; b) для любого числа
; b) для любого числа 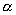 :
: 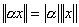 ; c) неравенство треугольника
; c) неравенство треугольника 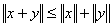 , - называется _______________ (ответ дайте одним словом)
, - называется _______________ (ответ дайте одним словом)
Многочлены Лежандра: Р0 = 1, Р1(х) = х, Р2 = 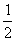 (3х2 - 1). Разложение элемента f(x) = 3x2 -x по многочленам Лежандра имеет вид:
(3х2 - 1). Разложение элемента f(x) = 3x2 -x по многочленам Лежандра имеет вид:
f(x) = 2P0 + 3P2
f(x) = P0 + 2P1 + P2
f(x) = 3P0 + 2P1
f(x) = P0 -P1 + 2P2
Как можно завершить определение: ограниченным оператором метрического пространства называется оператор, который каждое ограниченное подмножество отображает в
ограниченное подмножество
некоторый шар
себя
компактное множество
Норма интегрального оператора Фредгольма с квадратично интегрируемым ядром К(t,s) не превосходит числа В = 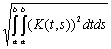 . Тогда норма интегрального оператора Фредгольма с ядром К(t,s) = (ts)6 в пространстве L2[0,1] ] B равна
. Тогда норма интегрального оператора Фредгольма с ядром К(t,s) = (ts)6 в пространстве L2[0,1] ] B равна
Многочлены Лежандра: Р0 = 1, Р1(х) = х, Р2 = 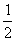 (3х2 - 1). Разложение элемента f(x) = 3x2 +5x +1 по многочленам Лежандра имеет вид:
(3х2 - 1). Разложение элемента f(x) = 3x2 +5x +1 по многочленам Лежандра имеет вид:
f(x) = P0 + 3P1 + 5P2
f(x) = 2P0 + 5P1 + 2P2
f(x) = 3P0 + 5P1 + P2
f(x) = 5P0 + 2P1 + 5P2
Скалярное произведение функций f(x) и g(x) в пространстве 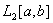 определяется по формуле: (f(x),g(x)) =
определяется по формуле: (f(x),g(x)) = 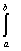 f(x)×g(x)dx. Тогда скалярное произведение элементов
f(x)×g(x)dx. Тогда скалярное произведение элементов 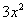 и
и 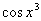 в пространстве
в пространстве 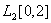 равно ___________ (укажите ответ в виде выражения)
равно ___________ (укажите ответ в виде выражения)
Укажите возможные связки в теореме. Подмножество 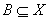 является замкнутым ___________ его дополнение
является замкнутым ___________ его дополнение 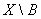 является открытым подмножеством. A) тогда и только тогда, когда …; B) при необходимом и достаточном условии, что…; С) если
является открытым подмножеством. A) тогда и только тогда, когда …; B) при необходимом и достаточном условии, что…; С) если
А) или С)
С)
В) и С)
A) или B)
Даны два множества 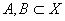 , причем хотя бы одно из них открыто. Тогда их объединение -
, причем хотя бы одно из них открыто. Тогда их объединение -
замкнутое множество, если замкнуто другое множество
открытое множество только, если открыто другое множество
открытое множество, независимо открыто ли другое множество
открытое множество только, если другое является его подмножеством
Неравенству треугольника удовлетворяют функции, определяющие
скалярное произведение
метрику
норму
расстояние между векторами
Уравнение 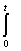 ln(t2+ts+s2)x(s)ds = t + 3 является интегральным уравнением уравнением Вольтера __________ (какого?) рода. Укажите порядок словом рода
ln(t2+ts+s2)x(s)ds = t + 3 является интегральным уравнением уравнением Вольтера __________ (какого?) рода. Укажите порядок словом рода
Точка х Î А называется предельной для подмножества В Í А, если любая e-окрестность точки х содержит точку множества В, отличную от точки х. Тогда множеством предельных точек множества всех рациональных чисел является множество
всех иррациональных чисел
всех рациональных чисел
всех вещественных чисел
Æ - пустое множество
Интегральное уравнение вида 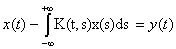 есть интегральное уравнение Фредгольма второго рода, когда ( выберите два верных условия)
есть интегральное уравнение Фредгольма второго рода, когда ( выберите два верных условия)
Укажите верные утверждения. Пусть вектор 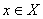 ортогонален к конечномерному подпространству
ортогонален к конечномерному подпространству 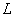 евклидова, или унитарного, пространства
евклидова, или унитарного, пространства  , тогда
, тогда
вектор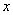 ортогонален каждому вектору подпространства
ортогонален каждому вектору подпространства
скалярное произведение вектора 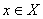 и любого вектора подпространства
и любого вектора подпространства 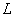 равно нулю
равно нулю
существует 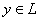 такой, что
такой, что 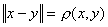
существует единственный 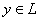 , которому вектор
, которому вектор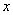 ортогонален
ортогонален
Известно, что расстояние от точки 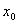 линейного нормированного пространства
линейного нормированного пространства  до гиперплоскости
до гиперплоскости 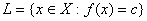 находится по формуле
находится по формуле 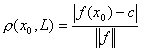 . Если
. Если 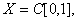
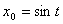 и
и 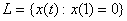 , то
, то 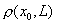 равно
равно
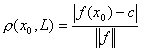 . Если
. Если sin1
cos1
1
1/3
Интегральное уравнение Фредгольма x(t) - l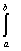 K(t,s)x(s)ds = y(t) c параметром l решается методом последовательных приближений при
K(t,s)x(s)ds = y(t) c параметром l решается методом последовательных приближений при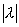 <
< 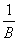 , где В =
, где В = 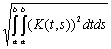 . Тогда интегральное уравнение Фредгольма x(t) - l
. Тогда интегральное уравнение Фредгольма x(t) - l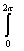 sint×sins×x(s) ds = y(t) решается методом последовательных приближений при l, меньшем
sint×sins×x(s) ds = y(t) решается методом последовательных приближений при l, меньшем
p
Интегральное уравнение 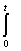 (2t2 - sins)x(s)ds = tgt является интегральным уравнением Вольтерра _____________ (какого? Ответ дайте словом) рода
(2t2 - sins)x(s)ds = tgt является интегральным уравнением Вольтерра _____________ (какого? Ответ дайте словом) рода
Предельными точками спектра самосопряженного вполне непрерывного линейного оператора могут быть
минус бесконечность 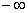
единица 1
ноль 0
плюс бесконечность 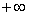
Установите соответствие между названием пространства и равенством, определяющем в нем норму
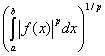
пространство непрерывных функций с равномерной нормой
пространство последовательностей с “p”-нормой
пространство непрерывных функций с интегральной нормой
Рассматриваются линейные уравнения первого рода 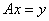 и второго рода
и второго рода 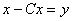 . Укажите верное утверждение:
. Укажите верное утверждение:
уравнение первого рода нельзя свести к уравнению второго рода, а уравнение второго рода можно свести к уравнению первого рода
переход одного вида уравнения в другое возможен лишь для специального класса операторов 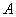 и
и 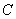
уравнение первого рода можно свести к уравнению второго рода, а уравнение второго рода нельзя свести к уравнению первого рода
уравнение первого рода можно свести к уравнению второго рода и уравнение второго рода можно свести к уравнению первого рода
Пусть  - произвольное множество. Функция
- произвольное множество. Функция 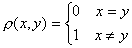 может определять
может определять
Завершите определение: точка 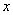 метрического пространства
метрического пространства  называется _________ (какой?) для отображения
называется _________ (какой?) для отображения 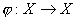 , если
, если 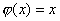
Коэффициент ряда Фурье элемента f(x) = x по ортогональной системе 1, coskx, sinkx, k = 1,2,… пространства L2[-p,p] при sin2x равен
-2
3
2
-1
Имеем линейное нормированное пространство 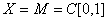 и определенный на
и определенный на 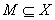 функционал
функционал 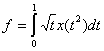 является
является
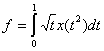 является
являетсяограниченным
непрерывным
линейным
вполне непрерывным
Пусть 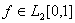 . Уравнение
. Уравнение 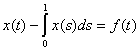 имеет решение, если интеграл
имеет решение, если интеграл 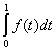 равен ______ (укажите число)
равен ______ (укажите число)
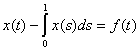 имеет решение, если интеграл
имеет решение, если интеграл 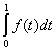 равен ______ (укажите число)
равен ______ (укажите число)Укажите верные утверждения. Формула 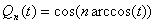 ,
, 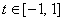 определяет многочлены:
определяет многочлены:
Чебышева
имеющие минимальную равномерную норму, среди многочленов вида 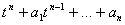
Лежандра
наилучшего приближения функций, непрерывных на отрезке 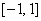
Для решения интегральных уравнений Фредгольма на практике применяют следующие способы:
используют аппроксимации функции рядами Фурье
используют разложение функции в ряд Тейлора
используют аппроксимацию ядра вырожденным ядром
рассматривают уравнение с параметром
Рассматривается линейный самосопряженный вполне непрерывный оператор 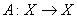 . Укажите верные утверждения:
. Укажите верные утверждения:
собственные значения такого оператора вещественны
оператор имеет по крайней мере одно отличное от нуля собственное значение
среди собственных значений обязательно есть ноль
каждому собственному значению соответствует единственный собственный вектор
Интегральное уравнение Фредгольма x(t) - l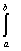 K(t,s)x(s)ds = y(t) c параметром l решается методом последовательных приближений при <
K(t,s)x(s)ds = y(t) c параметром l решается методом последовательных приближений при < 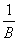 , где В =
, где В = 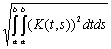 . Тогда интегральное уравнение Фредгольма x(t) - l
. Тогда интегральное уравнение Фредгольма x(t) - l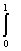 t4s5x(s)ds = y(t) решается методом последовательных приближений при l, меньшем
t4s5x(s)ds = y(t) решается методом последовательных приближений при l, меньшем
2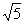
2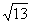
3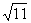
5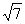
Спектр совпадает с множеством _________________(каких?) чисел (заполните пробел словом)
Пусть 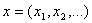 последовательность действительных или комплексных чисел. Тогда равенство
последовательность действительных или комплексных чисел. Тогда равенство 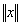 =
= 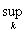
 определяет норму для пространств последовательностей:
определяет норму для пространств последовательностей:
стремящихся к нулю
с неотрицательными членами
сходящихся
ограниченных