Численные методы
Полную проблему собственных значений можно решать методом
вращений
Зейделя
степенным
Ньютона
Функция u(x,y) задана таблицей  Значение частной производной
Значение частной производной 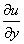 , вычисленное с помощью центральной разности в точке x = 0,6 y = 1,2, равно
, вычисленное с помощью центральной разности в точке x = 0,6 y = 1,2, равно
 Значение частной производной
Значение частной производной 1,4
1,6
1,5
2
Диагональная матрица - это квадратная матрица, у которой
на главной диагонали стоят только нулевые элементы
ненулевые элементы стоят только на главной диагонали
на главной диагонали стоят только положительные элементы
на главной диагонали стоят только единицы
Для задачи Коши 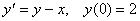 один шаг метода Эйлера с пересчетом с h = 0,2 дает результат для y(0,2), равный
один шаг метода Эйлера с пересчетом с h = 0,2 дает результат для y(0,2), равный
2,05
2,2
2,4
2,1
Заданы системы линейных уравнений 1)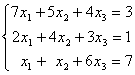 2)
2) 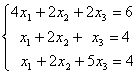 3)
3) 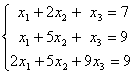 . Свойством диагонального преобладания обладают матрицы систем
. Свойством диагонального преобладания обладают матрицы систем
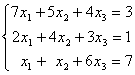 2)
2) 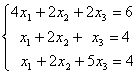 3)
3) 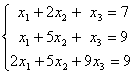 . Свойством диагонального преобладания обладают матрицы систем
. Свойством диагонального преобладания обладают матрицы систем2 и 3
1 и 2
только 2
только 1
Матрица А = 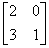 называется
называется
симметричной
диагональной
верхней треугольной
нижней треугольной
Локальная погрешность решения задачи Коши обыкновенного дифференциального уравнения методом Рунге - Кутта имеет порядок, равный
5
3
6
4
Формула метода Ньютона для нелинейного уравнения F( x ) = 0 имеет вид:
xk+1 = xk ( 1 − F( xk ) )
xk+1 = xk + F′( xk ) / F( xk )
xk+1 = xk − F( xk ) / F′( xk )
xk+1 = F( xk )
Задана табличная функция y = f(x) 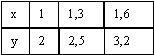 Линейная интерполяция дает значение y (1,4), равное
Линейная интерполяция дает значение y (1,4), равное
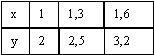 Линейная интерполяция дает значение y (1,4), равное
Линейная интерполяция дает значение y (1,4), равное2,5667
2,733
2,6667
2,8
Рассматривается задача Коши для системы дифференциальных уравнений 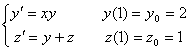 Один шаг метода Эйлера с h = 0,1 дает результат
Один шаг метода Эйлера с h = 0,1 дает результат
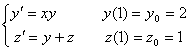 Один шаг метода Эйлера с h = 0,1 дает результат
Один шаг метода Эйлера с h = 0,1 дает результатФормула метода Эйлера для решения задачи Коши обыкновенного дифференциального уравнения имеет вид
Для задачи Коши 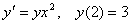 один шаг метода Эйлера с h = 0,1 дает результат для y(2,1), равный
один шаг метода Эйлера с h = 0,1 дает результат для y(2,1), равный
4,2
3,2
3,5
4,1
Якобиан системы нелинейных уравнений в данной точке представляет собой
вектор
число
матрицу
функцию
Ленточная матрица - это квадратная матрица, у которой
ниже главной диагонали все элементы равны единице (образуют «ленту из единиц)
выше главной диагонали все элементы равны нулю (образуют «нулевую ленту)
все ненулевые элементы параллельны главной диагонали, а остальные элементы равны нулю
выше главной диагонали все элементы равны единице (образуют «ленту из единиц)
Задана система линейных уравнений 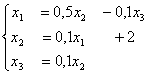 Один шаг метода Зейделя с начальным приближением { 0 ; 1 ; 0 } дает следующее первое приближение
Один шаг метода Зейделя с начальным приближением { 0 ; 1 ; 0 } дает следующее первое приближение
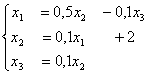 Один шаг метода Зейделя с начальным приближением { 0 ; 1 ; 0 } дает следующее первое приближение
Один шаг метода Зейделя с начальным приближением { 0 ; 1 ; 0 } дает следующее первое приближение{ 0,5 ; 2 ; 0,0205 }
{ 0,5 ; 2,05 ; 0,205 }
{ 0,3 ; 2,05 ; 2 }
{ 0,5 ; 2 ; 0,1 }
При вычислении интеграла 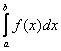 методом Гаусса исходный интервал интегрирования [a, b] необходимо преобразовать к интервалу
методом Гаусса исходный интервал интегрирования [a, b] необходимо преобразовать к интервалу
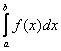 методом Гаусса исходный интервал интегрирования [a, b] необходимо преобразовать к интервалу
методом Гаусса исходный интервал интегрирования [a, b] необходимо преобразовать к интервалу[-1, 0]
[-1, 1]
[-0,5; 0,5]
[0, 1]
Результат вычисления интеграла 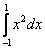 методом Симпсона с разбиением на два интервала (h = 1) равен
методом Симпсона с разбиением на два интервала (h = 1) равен
3∕4
1
0,5
2∕3
Достаточным условием сходимости метода Ньютона для уравнения F( x ) = 0 будет выполнение условия
Функция u(x,y) задана таблицей  Значение частной производной
Значение частной производной 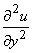 , вычисленное с помощью центральной разности в точке x = 0,6 y = 1,2, равно
, вычисленное с помощью центральной разности в точке x = 0,6 y = 1,2, равно
 Значение частной производной
Значение частной производной 11
9
10,56
10
Для величин x = 2 , y = 1 , z = 2 заданы их относительные погрешности δ(x) = 0,005 ; δ(y) = 0,001 ; δ(z) = 0,002 . Относительная погрешность произведения δ( x ∙ y ∙z) равна
0,0001
0,0000002
0,0002
0,008
Погрешность математической модели является
возрастающей
вычислительной
неустранимой
регулируемой
Дано нелинейное уравнение cos2x - 2x + π ∕ 4 = 0 и начальное условие x0 = π∕4. Первое приближение метода Ньютона x1 будет равно
3π ∕ 4
π ∕ 2
3π ∕ 16
5π ∕ 16
Уравнение нестационарной теплопроводности является
эллиптическим
гиперболическим
смешанным
параболическим
Для величин x = 2 и y = 1 известны относительные погрешности δ(x) = 0,001 и δ(y) = 0,002. Относительная погрешность разности δ( x - y ) равна
0,004
0,0002
0,001
0,003
Задана линейная система 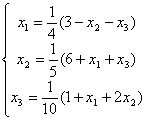 . Начиная с начального значения x1(0) = x2(0) = x3(0) = 0 , один шаг метода Зейделя { x1(1), x2(1), x3(1)} будет равен
. Начиная с начального значения x1(0) = x2(0) = x3(0) = 0 , один шаг метода Зейделя { x1(1), x2(1), x3(1)} будет равен
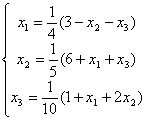 . Начиная с начального значения x1(0) = x2(0) = x3(0) = 0 , один шаг метода Зейделя { x1(1), x2(1), x3(1)} будет равен
. Начиная с начального значения x1(0) = x2(0) = x3(0) = 0 , один шаг метода Зейделя { x1(1), x2(1), x3(1)} будет равен{ 0,75 ; 1,35 ; 0,05 }
{ 0,75 ; 1,2 ; 0,445 }
{ 0,75 ; 1,2 ; 0,1 }
{ 0,75 ; 1,35 ; 0,445 }
Краевую задачу для уравнения Лапласа 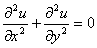 называют задачей Дирихле, если граничные условия имеют вид
называют задачей Дирихле, если граничные условия имеют вид
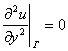
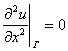
В квадратурном методе Гаусса узловые точки на отрезке интегрирования расположены
в точках, являющихся корнями многочлена Лежандра
в точках, являющихся корнями многочлена Чебышева
неравномерно, со сгущением к середине отрезка
равномерно
Разностный метод для решения задачи Коши, имеющий вид , является
трехшаговым
двухшаговым
многошаговым
одношаговым
Интерполяцией называется такая аппроксимация исходной функции f(x) интерполирующей функцией φ(x), при которой
Рассматривается задача Коши для системы дифференциальных уравнений 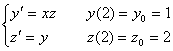 Один шаг метода Эйлера с h = 0,2 дает результат
Один шаг метода Эйлера с h = 0,2 дает результат
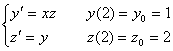 Один шаг метода Эйлера с h = 0,2 дает результат
Один шаг метода Эйлера с h = 0,2 дает результатАппроксимация называется непрерывной, если аппроксимирующая функция φ(x)
аппроксимирует исходную непрерывную функцию f(x)
является непрерывной
строится на отрезке [a, b]
является многочленом
Задано нелинейное уравнение вида x = x3 - 2x и начальное приближение x0 = 2. Один шаг метода простой итерации дает
x1 = 4
x1 = 10
x1 = 2,5
x1 = 1
Явная разностная схема для решения уравнения теплопроводности является
абсолютно неустойчивой
условно устойчивой
абсолютно устойчивой
устойчивой при 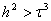
При вычислении интеграла 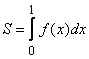 подынтегральная функция задана таблицей
подынтегральная функция задана таблицей 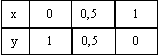 Метод трапеций с h = 0,5 дает значение интеграла
Метод трапеций с h = 0,5 дает значение интеграла
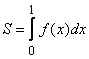 подынтегральная функция задана таблицей
подынтегральная функция задана таблицей 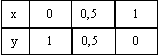 Метод трапеций с h = 0,5 дает значение интеграла
Метод трапеций с h = 0,5 дает значение интеграла0,5
1
2∕3
1,5
Разностное уравнение 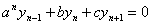 является уравнением
является уравнением
с переменными коэффициентами
с постоянными коэффициентами
n-го порядка
первого порядка
Собственные значения матрицы А расположены в порядке убывания λ1 > λ2 ≥ λ3 ≥ … ≥ λn . Степенной метод нахождения λ1 сходится, если
Интегральное уравнение 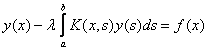 является
является
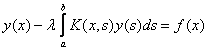 является
являетсяуравнением Гаусса первого рода
интегральным уравнением Фредгольма второго рода
интегральным уравнением Фредгольма первого рода
уравнением Ньютона
Достаточные условия сходимости метода Зейделя для системы линейных уравнений с матрицей A заключаются в том, что
aii ≠ 0 ( i = 1, 2, . . . n )
Для таблично заданной функции 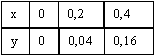 вычисление y(0,1) с помощью линейной интерполяции дает результат
вычисление y(0,1) с помощью линейной интерполяции дает результат
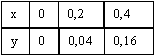 вычисление y(0,1) с помощью линейной интерполяции дает результат
вычисление y(0,1) с помощью линейной интерполяции дает результат0,03
0,22
0,02
0,01
При вычислении интеграла 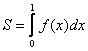 подынтегральная функция задана таблицей
подынтегральная функция задана таблицей 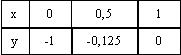 Метод Симпсона с h = 0,5 дает значение интеграла
Метод Симпсона с h = 0,5 дает значение интеграла
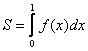 подынтегральная функция задана таблицей
подынтегральная функция задана таблицей 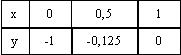 Метод Симпсона с h = 0,5 дает значение интеграла
Метод Симпсона с h = 0,5 дает значение интеграла-0,25
-0,3125
-0,375
-0,3
Дано уравнение x = sinx + 1 и начальное приближение x0 = π ⁄ 2 . Первое приближение x1 метода итераций равно
2
1
π
0
Даны линейные системы 1)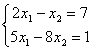 2)
2)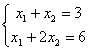 3)
3)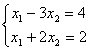 4)
4)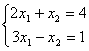 Свойством диагонального преобладания обладают системы
Свойством диагонального преобладания обладают системы
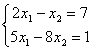 2)
2)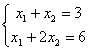 3)
3)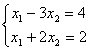 4)
4)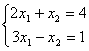 Свойством диагонального преобладания обладают системы
Свойством диагонального преобладания обладают системы1 и 4
1 и 2
1, 3 и 4
3 и 4
Рассматривается задача Коши для системы дифференциальных уравнений 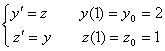 Один шаг метода Эйлера с h = 0,1 дает результат
Один шаг метода Эйлера с h = 0,1 дает результат
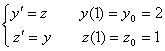 Один шаг метода Эйлера с h = 0,1 дает результат
Один шаг метода Эйлера с h = 0,1 дает результат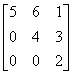 называется
называется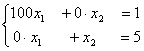 будет равна
будет равна