Теория вероятностей, математическая статистика и случайные процессы
Вероятность наступления некоторого события не может быть равна
0,7
1
0,3
1,7
Вероятность того, что дом может сгореть в течение года, равна 0,01. Застраховано 300 домов. Для вычисления вероятности того, что сгорит не более 4 домов, следует использовать …
формулу Пуассона
формулу полной вероятности
таблицу плотности нормального распределения
локальную формулу Муавра-Лапласа
В первом игровом автомате можно выиграть с вероятностью 0,6; а во втором – с вероятностью 0,3. Вероятность выиграть одновременно в обоих автоматах равна
0,3
0,82
0,9
0,18
Случайная величина распределена равномерно на отрезке [0;5]. Найти вероятность, что случайно брошенная точка попадёт на отрезок [1;3]. Ответ дайте десятичной дробью
Выберите верные утверждения
3! = 3
2! = 2
1! = 1
0! = 0
В урне находятся 5 белых, 4 зеленых и 3 красных шара. Наугад извлекается один шар. Вероятность того, что он будет цветным, равна
0,5
1
Из колоды в 32 карты извлекают одну карту. Вероятность того, что извлеченная карта – туз, равна
0,125
0,2
0,4
0,25
В урне 4 билета. Из них 2 выигрышных. Вынимаем три билета случайным образом. Р3 – вероятность вынуть три выигрышных билета. Р2 – вероятность вынуть два выигрышных билета. Р1 – вероятность вынуть один выигрышный билет. Р0 – вероятность, что все билеты не выиграли. Выберите верные утверждения
Р1 = 0,5
Р0 = 0,1
Р2 = 0,4
Р3 = 0
Вероятность того, что студент сдаст экзамен по математике, равна 0,5, а экзамен по иностранному языку – 0,6. Вероятность того, что он сдаст хотя бы один экзамен, равна
0,5×0,6
1 – 0,5×0,6
0,5 + 0,6 – 0,3
0,5 + 0,6
На отрезке длиной 20 см помещен меньший отрезок L длиной 10 см. Найти вероятность того, что точка, наудачу брошенная на большой отрезок, попа дет также и на меньший отрезок. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его располо жения Ответ дайте десятичной дробью
Игральная кость брошена 3 раза. Тогда вероятность того, что «шестерка» выпадет хотя бы один раз, равна …
В первом ящике 7 красных и 11 синих шаров, во втором – 5 красных и 9 синих. Из произвольного ящика достают один шар. Вероятность того, что он синий, равна…
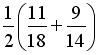
По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию, равны 0,1 и 0,05. Тогда вероятность банкротства обоих предприятий равна
0,855
0,05
0,15
0,005
Вероятность появления события А в 20 независимых испытаниях, проводимых по схеме Бернулли, равна 0,6. Тогда дисперсия числа появлений этого события равна
0,48
4,8
0,03
12
Случайная величина Х называется нормированной, если
МХ = 0; DX = МX2
МХ = 1; DX = МХ
МХ = 0; DX =1
МХ = 1; DX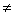 
0
0Игральный кубик бросают один раз. Вероятность того, что на верхней грани выпадет число очков, равное трем или пяти, равна
2/3
1/6
1/3
1/2
В урне 4 билета. Из них 2 выигрышных. Вынимаем три билета случайным образом. Р3 – вероятность вынуть три выигрышных билета. Р2 – вероятность вынуть два выигрышных билета. Р1 – вероятность вынуть один выигрышный билет. Р0 – вероятность, что все билеты не выиграли. Выберите верные утверждения
Р0 = 0
Р1 = 0,4
Р2 = 0,4
Р3 = 0
Вероятность попадания в десятку для некоторого стрелка равна 0,7. Стрелок стреляет дважды по мишени. Вероятность того, что стрелок попадёт дважды, равна
0,3
0,21
0,5
0,49
В тире лежат два ружья. Вероятность стрелку попасть из первого ружья 0,9. Вероятность стрелку попасть из второго ружья 0,6. Стрелок заходит в тир, наугад берёт ружьё, два раза стреляет. Р0 – вероятность, что попаданий нет. Р1 – вероятность, что попал один раз. Р2 – вероятность двух попаданий
Р0
0,585
Р1
0,33
Р2
0,085
Дан закон распределения вероятностей дискретной случайной величины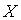 
: 
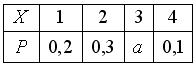Тогда значение 
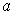равно…
: Тогда значение равно…0,6
0,4
0,3
– 0,6
В партии из 10 деталей 8 стандартных. Наугад выбирается две детали. Вероятность того, что обе детали будут стандартными, равна
0,9
0,8
Случайная величина Х распределена равномерно на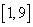 
, тогда вероятность попасть в интервал [4,5] равна
, тогда вероятность попасть в интервал [4,5] равна0,25
0,125
0,2
0,1
Вероятность достоверного события равна
0
1
0,996
– 1
Стрелок попадает в цель с вероятностью 0,5. Стрелок стреляет три раза. Р3 – вероятность попасть три раза. Р2 – вероятность попасть два раза, один раз смазать. Р1 – вероятность попасть один раз, два раза смазать. Р0 – вероятность все три раза смазать. Выберите верные утверждения
Р2 = 0,475
Р0 = 0,125
Р3 = 0,1
Р1 = 0,375
Дискретная случайная величина Х имеет закон распределения вероятностей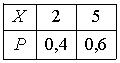 
. Математическое ожидание М(Х) этой случайной величины равно
. Математическое ожидание М(Х) этой случайной величины равно3,8
3,2
7
1
Монета брошена 7 раз. Тогда вероятность того, что «герб» выпадет ровно 6 раз, равна…
Стрелок попадает в цель с вероятностью 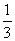. Стрелок стреляет три раза. Р3 – вероятность попасть три раза. Р2 – вероятность попасть два раза, один раз смазать. Р1 – вероятность попасть один раз, два раза смазать. Р0 – вероятность все три раза смазать. Выберите верные утверждения
. Стрелок стреляет три раза. Р3 – вероятность попасть три раза. Р2 – вероятность попасть два раза, один раз смазать. Р1 – вероятность попасть один раз, два раза смазать. Р0 – вероятность все три раза смазать. Выберите верные утвержденияР3 =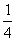 
Р1 =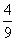 
Р2 =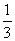
Р0 =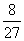 
График плотности распределения вероятностей непрерывной случайной величины Х, распределённой равномерно в интервале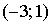 
, имеет вид: 
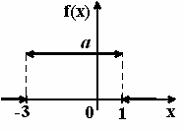Тогда значение а равно
, имеет вид: Тогда значение а равно0,4
0,2
1
0,25
Непрерывная случайная величина X задана плотностью распределения вероятностей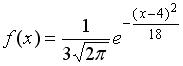 
.Тогда математическое ожидание этой нормально распределённой случайной величины равно …
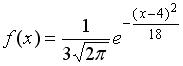.Тогда математическое ожидание этой нормально распределённой случайной величины равно …4
18
3
9
Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет не более трех очков, равна…
Бросаются 2 кубика. Вероятность, что сумма выпавших очков равна 3, равна. Ответ дайте в виде обыкновенной дроби a/b
В колоде 32 карты. Вынимаем две карты. Р0 – вероятность, что червей нет. Р1 – вероятность, что вынута одна черва. Р2 – вероятность, что вынуты две червы
Р1
Р0
Р2
Число опечаток на одной странице – случайная величина, распределенная по закону Пуассона c l = 0,5. Вероятность того, что на случайно выбранной странице будет 2 опечатки, равна
0,05
e-0,50,5
(0,5)2
Бросают 2 монеты. События А – «цифра на первой монете» и В – «цифра на второй монете» являются:
несовместными
независимыми
совместными
зависимыми
В аквариуме плавают рыбки: 10 меченосцев и 6 вуалехвостов. Наугад ловится одна рыбка. Вероятность того, что это будет меченосец, равна
0,9
0,5
Вероятность невозможного события равна…
1
0
0,001
– 1
Игральный кубик бросают один раз. Вероятность того, что на верхней грани выпадет число очков, равное двум или четырем, равна
2/3
1/3
1/2
1/6
Футбольная команда выиграет первый матч с вероятностью 0,9; а второй – с вероятностью 0,4. Вероятность того, что команда выиграет оба матча, равна
0,5
1,3
0,64
0,36
Укажите соответствие между формулами и их значениями
0!
2
3!
6
2!
1
Вероятность невозможного события равна
1
– 1
0
0,01
Первый студент успешно ответит на данный тест с вероятностью 0,5; второй – с вероятностью 0,7. Вероятность того, что оба студента ответят успешно, равна
0,035
0,7
1,2
0,35
Случайная величина имеет плотность распределения { f(x) = a при x Î [1,3]; f(x) = 0 при x Ï [1,3]}. Тогда параметр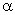 
равен
равен2
0,5
3
1
По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию, равны 0,4 и 0,15. Тогда вероятность банкротства обоих предприятий равна
0,51
0,55
0,06
0,60
Дискретная случайная величина Х имеет закон распределения вероятностей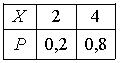 
Математическое ожидание М(Х) этой случайной величины равно
Математическое ожидание М(Х) этой случайной величины равно3,6
1
2,4
6
Если вероятность события А равна Р(1. , то вероятность противоположного события Р(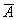
) определяется как
) определяется как1 – Р(1.
1 – 2Р(1.
1 – 0,5×Р(1.
2Р(1.
Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет менее шести очков, равна…
1
Два одноклассника поступают в институт на разные факультеты. Первый одноклассника поступит с вероятностью 0,5; второй – с вероятностью 0,6. Вероятность того, что оба одноклассника поступят, равна
0,03
0,3
1,1
0,7
Из 30 экзаменационных билетов студент хорошо выучил 8 билетов. Он вытаскивает один билет, вероятность того, что билет будет счастливым, равна
0,5
0,2
В первой урне 2 белых и 8 черных шаров. Во второй урне 5 белых и 5 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна…
0,7
0,4
0,35
0,15
График плотности распределения вероятностей непрерывной случайной величины Х, распределённой равномерно в интервале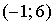 
, имеет вид: 
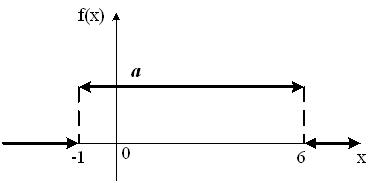Тогда значение a равно
, имеет вид: Тогда значение a равно1
