Теория вероятностей, математическая статистика и случайные процессы
В урне 100 шаров: 40 красных, 35 белых, 25 чёрных. Студент берёт наугад шар. Рк – вероятность вынуть красный шар, Рб – вероятность вынуть белый шар, Рч – вероятность вынуть чёрный шар
Рч
0,35
Рк
0,4
Рб
0,25
Вероятность вытащить качественную деталь из первого ящика равна 0,7; а из второго – 0,6. Из каждого ящика взяли по одной детали. Вероятность того, что обе они качественные, равна
1,3
0
0,42
0,58
Вероятность невозможного события равна…
1
0,002
0
– 1
В квадрат со стороной 6 вписан круг. 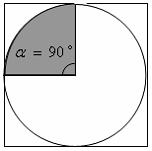 Тогда вероятность того, что точка, брошенная в квадрат, попадет в выделенный сектор, равна …
Тогда вероятность того, что точка, брошенная в квадрат, попадет в выделенный сектор, равна …
 Тогда вероятность того, что точка, брошенная в квадрат, попадет в выделенный сектор, равна …
Тогда вероятность того, что точка, брошенная в квадрат, попадет в выделенный сектор, равна …Изделия изготовляются независимо друг от друга. В среднем одно изделие из ста оказывается бракованным. Чему равна вероятность того, что из 200 взятых наугад изделий 2 окажутся неисправными? е-2 = 0,1353. Ответ дайте десятичной дробью
На ткацком станке нить обрывается в среднем 0,3 раза в течение часа работы станка. Вероятность того, что нить оборвется трижды за час, равна
0,3
e-0,3
В квадрат со стороной 12 брошена точка.  Тогда вероятность того, что она попадет в выделенную область, равна …
Тогда вероятность того, что она попадет в выделенную область, равна …
 Тогда вероятность того, что она попадет в выделенную область, равна …
Тогда вероятность того, что она попадет в выделенную область, равна …6
Из каждой из двух колод вынимают по одной карте. События А – «карта из первой колоды - туз» и В – «карта из второй колоды - дама» являются:
независимыми +
зависимыми
Совместными +
несовместными
В пирамиде 5 винтовок, 3 из которых снабжены оптическим прицелом. Вероятность попадания для стрелка при выстреле из винтовки с оптическим прицелом равна 0,95, из обычной винтовки – 0,7. Стрелок наудачу берет винтовку и стреляет. Найти вероятность того, что мишень будет поражена. Ответ дайте десятичной дробью
Два стрелка стреляют по одной мишени. Вероятность попадания первым стрелком равна 0,6. Вероятность попадания вторым стрелком равна 0,5. Р2 – вероятность попасть обоим стрелкам. Р1 – вероятность, что попал только один стрелок. Р0 – вероятность смазать обоим стрелкам. Р0,1 – вероятность первый смазал, второй попал. Выберите верные утверждения
Р2 = 0,3
Р1 = 0,4
Р0,1 = 0,3
Р0 = 0,2
Вероятность наступления некоторого события не может быть равна
0,3
1,3
0,2
1
Игральная кость бросается один раз. Тогда вероятность того, что выпадает четное число очков, равна
0,4
0,35
0,6
По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию, равны 0,2 и 0,15. Тогда вероятность банкротства обоих предприятий равна
0,03
0,35
0,68
0,3
Студент Иванов придет на лекцию с вероятностью 0,2; а студент Петров – с вероятностью 0,8. Вероятность того, что оба студента будут на лекции, равна
0,6
1
0,84
0,16
В колоде 36 карт. Вынимаем две карты. Р0 – вероятность, что тузов нет. Р1 – вероятность, что вынут один туз. Р2 – вероятность, что вынуты два туза
Р2
Р1
Р0
Стрелок попадает в цель с вероятностью 0,5. Стрелок стреляет три раза. Р3 – вероятность попасть три раза. Р2 – вероятность попасть два раза, один раз смазать. Р1 – вероятность попасть один раз, два раза смазать. Р0 – вероятность все три раза смазать. Выберите верные утверждения
Р1 = 0,475
Р3 = 0,1
Р0 = 0,125
Р2 = 0,375
А и В – случайные события. Верным является утверждение…
По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию, равны 0,2 и 0,25. Тогда вероятность банкротства обоих предприятий равна
0,05
0,5
0,6
0,45
Случайная величина 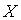 распределена равномерно на отрезке
распределена равномерно на отрезке 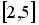 . Распределение случайной величины
. Распределение случайной величины 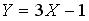 имеет...
имеет...
нормальное распределение на отрезке 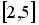
равномерное распределение на отрезке 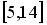
равномерное распределение на отрезке 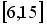
другой (кроме равномерного и нормального) вид распределения
В урне находится 5 белых и 5 черных шаров. Из урны вынимаются четыре шара. Вероятность того, что один шар будет белым, а 3 черными, равна …
По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию, равны 0,4 и 0,35. Тогда вероятность банкротства обоих предприятий равна
0,14
0,39
0,76
0,12
Дискретная случайная величина Х имеет закон распределения вероятностей 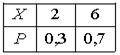 . Математическое ожидание М(Х) этой случайной величины равно
. Математическое ожидание М(Х) этой случайной величины равно
 . Математическое ожидание М(Х) этой случайной величины равно
. Математическое ожидание М(Х) этой случайной величины равно8
4,8
3,2
1
По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию, равны 0,3 и 0,25. Тогда вероятность банкротства обоих предприятий равна
0,75
0,075
0,55
0,525
Белый шар из первой урны можно вытащить с вероятностью 0,2; из второй – с вероятностью 0,7. Вытащили по одному шару из каждой урны. Вероятность вытащить два белых шара равна
0,86
0,9
0,14
1
Стрелок попадает в цель в среднем в 8 случаях из 10. Какова вероятность, что, сделав 3 выстрела, он 2 раза попадет, один раз промахнётся? Ответ дайте десятичной дробью
Пусть 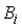
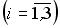 - события, заключающиеся в том, что произошел обрыв в цепи сопротивлений
- события, заключающиеся в том, что произошел обрыв в цепи сопротивлений 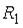 ,
, 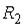 или
или 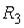
 Событие
Событие  - за время
- за время  произошел обрыв между точками
произошел обрыв между точками 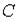 и
и 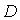 . Тогда
. Тогда 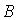 представимо через
представимо через 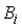 следующим образом …
следующим образом …
 Событие
Событие Выберите верные утверждения
В урне из 8 шаров имеется 3 красных. Наудачу берут два шара. Тогда вероятность того, что среди них ровно один красный шар, равна …
Вероятность наступления некоторого события не может быть равна
0
1,9
0,9
1
Укажите соответствие между формулами
n!
n×(n-1)×(n-2)×××3×2×1
Два стрелка стреляют по одной мишени. Вероятность попадания первым стрелком равна 0,6. Вероятность попадания вторым стрелком равна 0,5. Р2 – вероятность попасть обоим стрелкам. Р1 – вероятность, что попал только один стрелок. Р0 – вероятность смазать обоим стрелкам. Р0,1 – вероятность первый смазал, второй попал. Выберите верные утверждения
Р0,1 = 0,3
Р1 = 0,5
Р0 = 0,4
Р2 = 0,3
Студент Иванов придет на лекцию с вероятностью 0,2; а студент Петров – с вероятностью 0,8. Вероятность того, что оба студента будут на лекции, равна
1
0,84
0,16
0,6
Вероятность события может быть равна
любому числу из отрезка [0,1]
любому положительному числу
любому числу
любому числу отрезка [-1,1]
Игральный кубик бросают один раз. Вероятность того, что на верхней грани выпадет число очков, меньшее чем два, равна
2/3
1/6
1/3
5/6
График плотности распределения вероятностей непрерывной случайной величины Х, распределённой равномерно в интервале 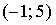 , имеет вид:
, имеет вид: 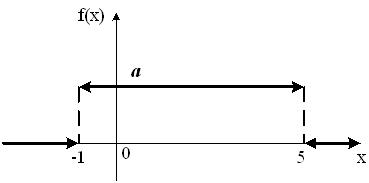 Тогда значение a равно
Тогда значение a равно
 Тогда значение a равно
Тогда значение a равно1
В колоде 36 карт. Вынимаем две карты. Р0 – вероятность, что червей нет. Р1 – вероятность, что вынута одна черва. Р2 – вероятность, что вынуты две червы.
Р2
Р0
Р1
Вероятность наступления некоторого события не может быть равна
0,6
1
3
0
Случайная величина распределена по нормальному закону, ее математическое ожидание равно 2, а дисперсия 16. Тогда ее плотность распределения имеет вид
f(x) = 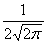
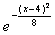
f(x) = 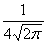
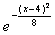
f(x) = 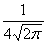
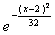
f(x) = 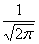
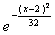
Вероятность попадания непрерывной случайной величины в интервал (a, b) выражается через функцию распределения следующей формулой
P (a < X < b) = F(b) – F(a)
P (a < X < b) = 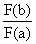
P (a < X < b) = 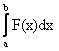
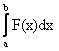
P (a < X < b) = 1 [F(b) – F(a)]
[F(b) – F(a)]
Вероятность вытащить бракованную деталь из первого ящика равна 0,2; а из второго – 0,3. Из каждого ящика взяли по одной детали. Вероятность того, что обе они бракованные, равна
0,94
0,06
0,5
0
Вероятность невозможного события равна
1
– 1
0
0,0001
Апостериорные вероятности Р(Нi/A) – это вероятности
гипотез после реализаций события
гипотез
полной группы событий до реализации опыта
группы событий
С первого станка на сборку поступает 60%, со второго – 40% всех деталей. Среди деталей первого станка 90% стандартных, второго – 80%. Взятая наудачу деталь оказалась стандартной. Тогда вероятность того, что она изготовлена на первом станке, равна …
Бросается 5 монет. Какова вероятность того, что выпадет 3 герба? Ответ дайте числом в виде обыкновенной дроби a/b
Функция распределения вероятностей дискретной случайной величины 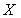 имеет вид
имеет вид 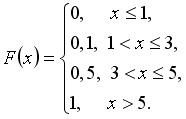 Тогда вероятность
Тогда вероятность 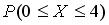 равна …
равна …
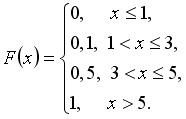 Тогда вероятность
Тогда вероятность 1
0,5
0,6
0,4
Для математического ожидания суммы случайной величины Х и постоянной С имеет место
M (X + C) = C
M (X + C) = MX
M (X + C) = MX – C
Монета брошена 7 раз. Тогда вероятность того, что «герб» выпадет ровно 3 раза, равна…
Выберите верные утверждения
5! = 120
2! = 2
4! = 4
3! = 3
В лотерее 1 000 билетов. На один билет выпадает выигрыш 5000 рублей, на десять билетов – выигрыши по 1 000 рублей, на пятьдесят билетов – выигрыши по 200 рублей, на сто билетов – выигрыши по 50 рублей; остальные билеты проигрышные. Покупается один билет. Тогда вероятность выигрыша 250 рублей равна …
1
0
0,15
Бросаются две симметричные монеты. Вероятность того, что выпадут и герб, и решка равна. Ответ дайте десятичной дробью