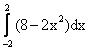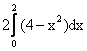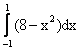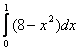Математический анализ (курс 3)
Ряды 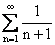 и
и 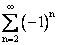
первый - расходится, второй - сходится
оба расходятся
первый - сходится, второй - расходится
оба сходятся
Для функции z=6x-x2-2y2+10
в точке (0,3) максимум
нет экстремума
в точке (3,0) максимум
в точке (3,0) минимум
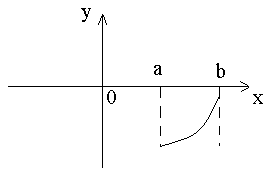
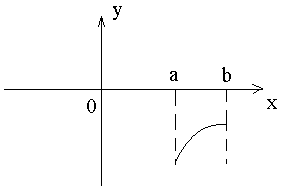
Укажите вид график функции, для которой на всём отрезке [a,b] одновременно выполняются три условия: у<0, y'>0,y''<0
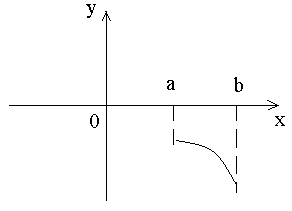
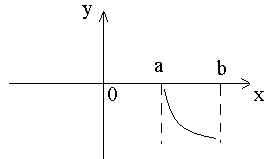
Функция f(x)=xlnx в точке x0=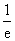 имеет
имеет
максимум
не имеет экстремума
не определена
минимум
При умножении числа 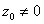 на число z радиус-вектор точки
на число z радиус-вектор точки 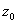 поворачивается на угол
поворачивается на угол
Длина дуги параболы y=x2 с концами в точках A(1,1) и B(2,4) вычисляется по формуле
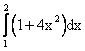
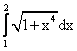
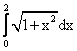
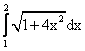
Точкой перегиба функции y=x3+3x является точка с координатами __________ (указать координаты)
Функция y=f(x) является убывающей на интервале, если на этом интервале
f´(x)=1
f´(x)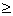 0
0
f´(x)<0
f´(x)= -1
Укажите правильные утверждения относительно сходимости числовых рядов А) 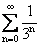 В)
В) 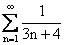
А и В - расходятся
А - сходится, В - расходится
А и В - сходятся
А - расходится, В - сходится
Комплексное число можно представить в следующих формах: _______________ формы
степенная
показательная
алгебраическая
тригонометрическая
Производная 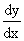 неявной функции 9x2+4y2=36 в точке P0(-1,8) равна ____/____ (указать число)
неявной функции 9x2+4y2=36 в точке P0(-1,8) равна ____/____ (указать число)
Расставить пределы интегрирования в двойном интеграле 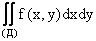 где D - прямоугольник с вершинами О(0,0), А(2,0), В(2,1), С(0,1)
где D - прямоугольник с вершинами О(0,0), А(2,0), В(2,1), С(0,1)
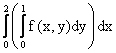
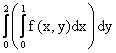
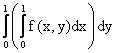
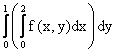
Частное решение линейного неоднородного дифференциального уравнения второго порядка y´´-y=x с начальными условиями y(0)=1, y´(0)=2 имеет вид ___________
2ex-e-x-x
ex-e-x
ex(1-2x)
1+2x
Объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями y=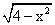 и x+y=2, равен разности интегралов
и x+y=2, равен разности интегралов
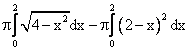
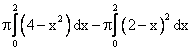
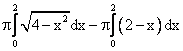
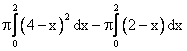
Установить соответствие между линейным однородным дифференциальным уравнением и видом его общего решения
y´´-2y´+3y=0
y=c1cos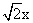 +c2sin
+c2sin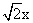
y´´-2y´=0
y=c1+c2e2x
y´´+2y=0
y=ex(c1cos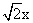 +c2sin
+c2sin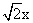 )
)
Уравнение нормали к поверхности В точке (4,3,4) имеет вид
3(x-4)+4(y-3)-6(z-4)=0
нельзя провести нормаль
Стационарной точкой функции z=x2+y2-xy+x+y+7 будет
М0(-1,-1)
М0(0,0)
М0(-1,0)
не существует стационарной точки
Область определения функции z=ln(x-y) - это
полуплоскость, расположенная под прямой y=x, причем сама прямая при рассмотрении не учитывается
прямая y=x
вся плоскость XoY
часть плоскости XoY, для которой y
Градиент скалярного поля u=x2-4xy5+3xy в произвольной точке имеет вид
Укажите соответствие между функциями и их точками экстремума
y=x2
нет
y=(x-1)2
x=1
y=x3
x=0
Полный дифференциал dz функции z=xy в точке P0(1,0) равен ___________ (указать число)
Для заданных функций указать точки, в которых имеются полюсы, и определить их порядок
полюсы первого порядка в точках 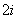 и
и 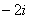
полюсы первого порядка в точках 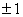
полюсы второго порядка в точках 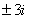
Функция y=arctgx на всей числовой оси
имеет максимум
монотонно возрастает
монотонно убывает
имеет минимум
Область определения функции 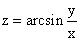 - это
- это
часть плоскости, удовлетворяющую условию 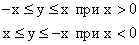
часть плоскости, удовлетворяющая условию 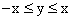
часть плоскости, удовлетворяющая условию 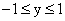
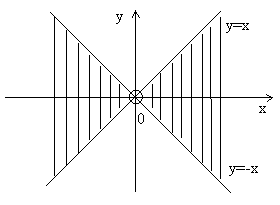
Функция 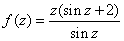 обладает свойствами:
обладает свойствами:
точка z1=π есть полюс первого порядка
точка z1= π является устранимой особой точкой
точка z0=0 является устранимой особой точкой
в области 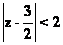 имеет две особые точки z0=0 и z1=π
имеет две особые точки z0=0 и z1=π
точка z0=0 является полюсом первого порядка
Наибольшая скорость возрастания скалярного поля z=x2+3xy-y2 при переходе через точку P0(1,2) равна
1
Следующие свойства справедливы для функции sinz:
функция sinz ограничена при всех z
функция разлагается в ряд Тейлора 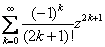
этот ряд сходится при любом значении z
Площадь четверти круга с центром в точке О(0,0) и радиуса 3 вычисляется по формуле
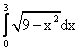
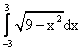
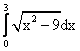
Установить соответствие между интегралами
-ctgx+c
-cosx+c
tgx+c
ln|sinx|+c
Укажите соответствие между уравнениями и их названиями
уравнение нормали к поверхности F(x,y,z)=0 в точке M0(x0,y0,z0)
уравнение нормали к поверхности z=f(x,y) в точке P0(x0,y0)
уравнение касательной плоскости к поверхности z=f(x,y) в точке P0(x0,y0)
Производная скалярного поля z=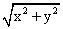 в точке (x0,y0) по направлению вектора
в точке (x0,y0) по направлению вектора 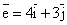 равна
равна
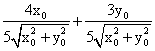
1
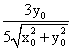
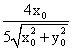
Коэффициент a3 разложения функции f(x)=3x+1 при 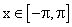 в ряд Фурье равен ____________ (указать число).
в ряд Фурье равен ____________ (указать число).
Множество первообразных функции 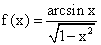 имеет вид
имеет вид
2arcsin2x+c
2arcsinx+c
Предел 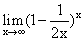 равен е в степени (укажите число в виде числа с точностью до десятой)
равен е в степени (укажите число в виде числа с точностью до десятой)
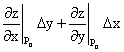
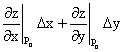
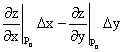
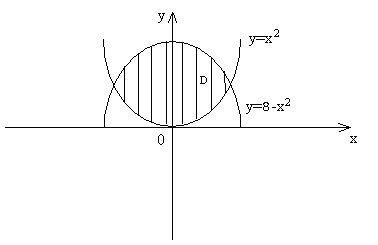 определяется интегралом
определяется интегралом