Математический анализ (курс 3)
Система дифференциальных уравнений 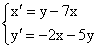
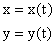 эквивалентна уравнению вида
эквивалентна уравнению вида
x´´-12x´+37x=0
x´´+37x=0
x´´+12x´+37x=0
x´´-12x´=0
Ряды 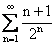 и
и 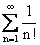
первый - расходится, второй - сходится
первый - сходится, второй - расходится
оба расходятся
оба сходятся
Производная скалярного поля z=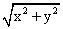 в точке (-1,1) по направлению вектора
в точке (-1,1) по направлению вектора 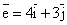 равна
равна
1
Найти частное комплексных чисел в алгебраической форме и указать соответствие между числами и их частным
Решением дифференциального уравнения 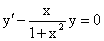 при начальном условии y(0)=1 будет функция ____________
при начальном условии y(0)=1 будет функция ____________
y=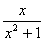
y=1+x2
y=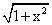
y=1-x
Модуль градиента скалярного поля z=arcсos(xy) в точке P0(0,1) равен _________ (указать число)
Производная скалярного поля z=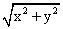 в точке (1,1) по направлению биссектрисы первого координатного угла равна
в точке (1,1) по направлению биссектрисы первого координатного угла равна
не существует
-1
0
1
«а» и «в» - высказывания, «а» - ложно, «в» - истинно. Высказывание «а» и «в» истинно или ложно? Какая операция использована?
истинно, конъюнкция
ложно, конъюнкция
ложно, дизъюнкция
истинно, дизъюнкция
Следующие свойства справедливы для функции ez
функция непериодична
функция ez в точке z=iπ равна -1
функция периодична
Объем тела, образованного вращением фигуры, ограниченной одной полуволной синусоиды y=sinx 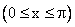 и отрезком
и отрезком 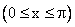 оси Ох, вокруг оси Ох равен ___________
оси Ох, вокруг оси Ох равен ___________
3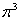
Установите соответствие между функциями z=f(x,y) и значениями градиентов
z=sin(2x-3y)
gradz=cos(2x+3y)( 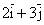 )
)
z=ln(3x-y+1)
gradz=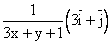
z=ln(3x+y+1)
gradz=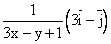
z=sin(2x+3y)
gradz=cos(2x-3y)(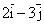 )
)
Уравнение касательной плоскости к сфере x2+y2+z2=27 в точке M0(3,3,3) имеет вид
(x-3)+(y-3)=z-3
x+y+z-9=0
в точке M0 нельзя провести касательную плоскость
6(x-3)+6(y-3)+6(z-3)=0
Производная функции y=3-xarctg(1-x) в точке x=1 равна
3 arctg 0
-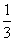
-3 ln 3
-3 (ln3 + 1)
Областью определения функции 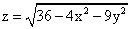 является множество
является множество
совокупность точек плоскости, лежащих внутри и на границе эллипса с центром в точке О(0,0) и полуосями 3 и 2
Область определения функции 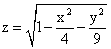 есть
есть
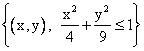
2 и 3
внутренность окружности центром в точке (2,3) и радиуса 1.
внутренность окружности с центром в точке (1,0) и радиуса 2.
внутренность эллипса (включая границу) с центром в точке О(0,0) и полуосями
Производная 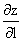 скалярного поля z=2x3-5y2 в точке (1,1) в направлении, задаваемом вектором
скалярного поля z=2x3-5y2 в точке (1,1) в направлении, задаваемом вектором 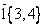 , равна
, равна
-22
-26
0
Установите соответствие между функциями и значениями частных производных в данной точке
z=ln(x2+y2), P1(-1,2)

z=tgxy, P0(0,1)
z=tgxy, P0(1,1)
Частная производная функции z=xy по переменной х в точке P0(2,1) равна
0
не существует
1
2
Горизонтальной асимптотой графика функции y=xe-x является прямая ______________ (написать уравнение)
Достаточным условием экстремума функции z=f(x,y) в точке P0(x0,y0) является



Даны множества А и В. Тогда множество С, изображенное на рисунке 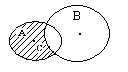 является
является
 является
являетсяУстановить соответствие между функциями комплексного переменного и их особенностями в точке 0
существенная особенность
устранимая особенность
sin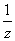
полюс
Производная скалярного поля u=3xy2+3yz2 в точке P0(1,0,-1) в направлении единичного вектора 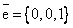 равна
равна
1
0
-6
12
Линией уровня функции Z=ln(x2+y2) является
окружность с центром в начале координат и радиусом с
точка О(0,0)
круг с центром в начале координат и радиусом с.
Решение задачи Коши y´´-4y´+4y=0, y(0)=1, y´(0)=3 имеет вид ________________
e(1+x)
e2x(1+x)
e2x
(1+x)
При x®0 бесконечные малые 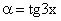 и
и 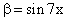
эквивалентны
β более высокого порядка, чем α
одного порядка
α более высокого порядка, чем β
Свободный член а0 ряда Фурье функции f(x)=-3x(-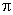
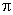 ), T=2
), T=2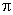 равен __________ (вставить число)
равен __________ (вставить число)
Если f(x)=x3-1, то коэффициент а4 разложения данной функции в ряд Тейлора по степеням (х+1) равен __________ (указать число).
Необходимым условием существования экстремума функции f(x) в точке x0 является условие
x0- стационарная точка функции f(x)
f´(x0)=0
f´(x0)>0
f´(x0)=1
Расставить пределы интегрирования в двойном интеграле где D - треугольник с вершинами О(0,0), А(1,0), В(1,1)
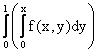 dx
dx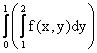 dx
dx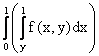 dy
dy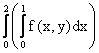 dy
dyРяд Фурье функции f(x)=|x| (-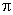
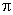 ), T=2
), T=2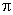 , в точке x0= -
, в точке x0= -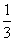 сходится к значению
сходится к значению
0
- 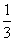
1
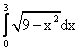 равен _________
равен _________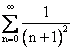
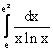 равен__________ (указать число)
равен__________ (указать число)