Математический анализ (курс 3)
Точка P0(x0,y0) называется точкой максимума функции z=f(x,y), если
существует 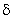 -окрестность
-окрестность 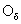 (P0) точки P0 такая, что значение функции f(P0) меньше любого значения f(P),
(P0) точки P0 такая, что значение функции f(P0) меньше любого значения f(P), 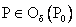
существует 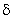 -окрестность
-окрестность 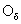 (P0) точки P0 такая, что значение функции f(P0) больше любого значения f(P),
(P0) точки P0 такая, что значение функции f(P0) больше любого значения f(P), 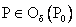
значение функции f(P0) больше всех значений функции f(P)
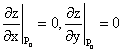
Областью определения функции z=ln(x2+y2) является множество
вся плоскость XoY, кроме точки О(0,0)
вся плоскость XoY
Общее решение уравнения y´´+y=x+2 имеет вид
c1cosx+c2sinx-x+2
ccosx+x+2
c1cosx+c2sinx+x+2
c1sinx+c2ex+x+2
Необходимым условием существования экстремума функции y=f(x) в точке x0 является условие
f´´(x0)=0
f´(x0)=1
f´(x0)>0
f´(x0)=0
Минимальные значения функции z=2x2-2xy+2y2-2x-2y+1 равно ___________ (указать число)
Частная производная функции z=ln(x2+y3) по переменной y в точке M0(1,-2) равна ________ (вставить число в виде …/…)
Установить соответствие между аналитичностью функции f(z)=w и областями на плоскости
аналитична в области 1<|z|<2
аналитична в области 0<|z-3|<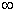
аналитична в области 2<|z|<4
Частная производная функции z=xy по переменной y в точке P0(2,1) равна
1
2ln2
2
0
Укажите правильное утверждение относительно сходимости числовых рядов А) 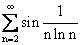 В)
В) 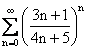
А - сходится, В - расходится
оба ряда сходятся
оба ряда расходятся
А - расходится, В - сходится
При x®0 бесконечно малые α=ln(1+2x) и β=arcsin2x
эквивалентны
несравнимы
α более высокого порядка, чем β
β более высокого порядка, чем α
Область определения функции z=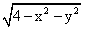 есть круг с центром в точке О(0,0) и радиуса ________ (указать число)
есть круг с центром в точке О(0,0) и радиуса ________ (указать число)
Общее решение дифференциального уравнения xy´´=y´ имеет вид
с1x+c2
с1x2+c2
x2+c
x+c1
Минимальное значение функции z=x2+xy+y2-2x-y равно ________ (указать число)
Стационарная точка функции z=x3+3x-5y2+4
(1,1)
(0,0)
(-1,0)
не существует
Найти область определения функции: 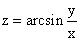
часть плоскости, удовлетворяющая условию y>x
часть на плоскости, удовлетворяющая условию -x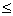 y
y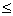 x
x
часть плоскости, примыкающая к оси Ох и заключенная между прямыми y=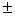 x, включая эти прямые и исключая начало координат
x, включая эти прямые и исключая начало координат
Производная 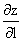 скалярного поля z=exy в точке P0(0,1) в направлении y=x равна
скалярного поля z=exy в точке P0(0,1) в направлении y=x равна
0
Функция y=2xe-x в точке x=1 имеет
возрастает на [0,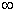 )
)
максимум
минимум
убывает на [0,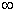 )
)
Из функций: А) 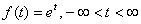 ; В)
; В) 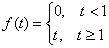 - функциями-оригиналами являются
- функциями-оригиналами являются
ни одна из А), В)
А)и В)
только В)
только А)
Производная скалярного поля z=ln(x+2y) в точке (1,2) по направлению биссектрисы первого координатного угла равна
0
Для функции z=2x+4y-2xy
функция имеет максимум в точке (0,0)
экстремум отсутствует
функция имеет максимум в точке (2,1)
функция имеет минимум в точке (0,0)
Найти соответствие между алгебраическими формами комплексных чисел и их модулями и аргументами
Уравнение касательной плоскости к поверхности 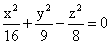 в точке (4,3,4) имеет вид
в точке (4,3,4) имеет вид
3x+4y-6z=0
9x+16y-18z+5=0
3x+4y-6z+4=0
Площадь, заключенная между кривыми y=2-x2 и y3=x2, вычисляется при помощи определенного интеграла
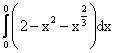
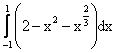
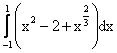
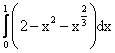
Уравнение касательной плоскости к поверхности z=xy в точке M0(-2,2,-4) имеет вид
2x-2y-z+12=0
x-y-z+8=0
2(x+2)-2(y-2)-(z-4)=0
Точка Z=0 является _____________ особой точкой функции 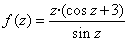 (вставить определение)
(вставить определение)
Установить соответствие между линейным однородным дифференциальным уравнением и его характеристическим многочленом
y´´+4y=0
k2-4k=0
y´´-4y´+4y=0
(k-2)2=0
y´´-4y´=0
k2+4=0
Модуль градиента скалярного поля u=x+2y+2z в произвольной точке равен ___________ (вставить число)
Общее решение линейного однородного дифференциального уравнения y´´-16y=0 имеет вид
c1e4x+c2e4x
e4x+e-4x
ce4x
c1e4x+c2e-4x
Функция f(x)=xlnx на промежутке (0,e] имеет наименьшее значение, равное
1
e
Укажите соответствие между функциями и значениями частной производной 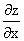 соответствующей функции в точке P0(1,1)
соответствующей функции в точке P0(1,1)
z=xy2
3
z=sinπxy
2
z=x2+y2
-π
x=3ex-y
1
Стационарная точка функции z=xy(9-x-y) (x>0, y>0) есть ___________ (указать координаты точки)
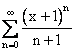 равен
равен
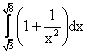
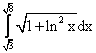
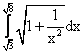
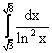
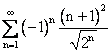 сходится ___________ (вставить слово)
сходится ___________ (вставить слово)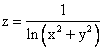 является множество
является множество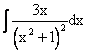 равен
равен