Алгебра и геометрия (курс 1)
Укажите верные соответствия:
система линейных уравнений
множество решений
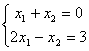
система несовместима
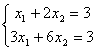
единственное решение
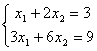
число решений
Установите соответствие между матрицами А и суммами элементов 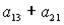 .
.
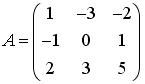
- 1
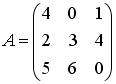
0
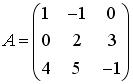
3
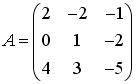
- 3
Матрицы 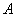 и
и 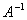 взаимно обратные Тогда произведение (det
взаимно обратные Тогда произведение (det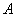 )(det
)(det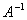 ) равно:
) равно:
зависит от определителя detA
1
зависит от порядка матрицы А
0
Даны матрицы 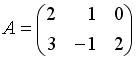 и
и 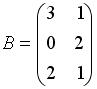 . Сумма элементов матрицы
. Сумма элементов матрицы 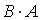 , расположенных на ее главной диагонали, равна …
, расположенных на ее главной диагонали, равна …
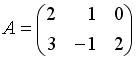 и
и 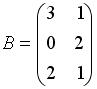 . Сумма элементов матрицы
. Сумма элементов матрицы Формула вычисления определителя третьего порядка  содержит следующие произведения: …
содержит следующие произведения: …
 содержит следующие произведения: …
содержит следующие произведения: …bfk
ceg
cdh
ach
Для системы уравнений 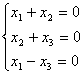 справедливы утверждения:
справедливы утверждения:
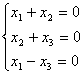 справедливы утверждения:
справедливы утверждения:решение системы единственно, 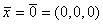
фундаментальная система решений состоит из 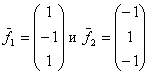
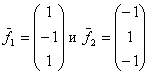
система имеет множество решений V и dim V = 2
Матрица 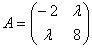 является вырожденной при
является вырожденной при 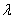 , равном:
, равном:
ни при каком значении 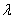
только при 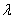 = 4
= 4
при всех вещественных 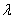
Общее решение системы уравнений 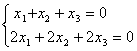 имеет вид:
имеет вид:
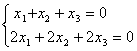 имеет вид:
имеет вид:
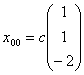 , где с – константа
, где с – константасистема имеет единственное решение (0, 0, 0)
Ранг вырожденной матрицы четвертого порядка:
равен 0
меньше 4
равен
равен 4
Система уравнений 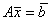 , где
, где 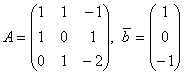 :
:
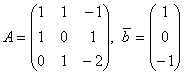 :
:несовместима
имеет решение 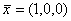
не может быть решена методом Крамера
имеет решение 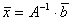
Теорема, определяющая критерий совместности системы линейных уравнений, носит название ________ (вставить название теоремы)
Если detA 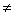 0, то:
0, то:
r(A) равен порядку матрицы А
строки матрицы линейно независимы
столбцы матрицы линейно зависимы
r(A) меньше порядка матрицы А
Общее решение уравнения с тремя неизвестными 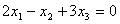 имеет вид:
имеет вид:
фундаментальная система решений состоит из 2-х векторов 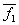 = (0, 0, 0),
= (0, 0, 0), 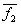 = (1, -1, -1)
= (1, -1, -1) 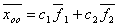
система имеет единственное нулевое решение 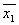 = (0, 0, 0)
= (0, 0, 0)
Система уравнений 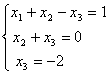 имеет:
имеет:
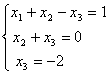 имеет:
имеет:множество решений
три решения
система несовместима
единственное решение
Одно уравнение с тремя неизвестными 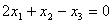 имеет:
имеет:
множество решений, общий вид решения 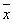 = С(1, 1, 3), где С – константа
= С(1, 1, 3), где С – константа
два решения 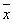 = (0, 0, 0) и
= (0, 0, 0) и 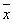 = (1, 1, 3)
= (1, 1, 3)
единственное тривиальное решение 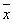 = (0, 0, 0)
= (0, 0, 0)
подпространство решений V и его размерность dimV = 2
Укажите систему линейных уравнений, подготовленную для обратного хода метода Гаусса.
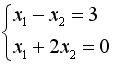
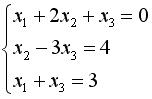
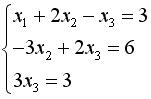
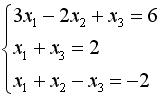
Система уравнений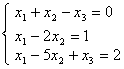 :
:
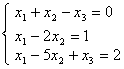 :
:решением системы является вектор 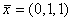
имеет множество решений
несовместима
имеет единственное решение
Элементарные преобразования над строками матрицы __________ ее ранга (слово)
Результатом выполнения действий в выражении 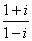 является число Z
является число Z
arg Z = 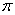
тригонометрическая форма Z имеет вид: 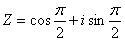
алгебраическая форма которого имеет вид Z = i
Квадратная матрица 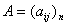 , для которой
, для которой 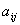 =
=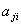 (для всех i, j) называется __________ матрицей
(для всех i, j) называется __________ матрицей
Система линейных уравнений совместима тогда и только тогда, когда ранг матрицы А __________ рангу расширенной матрицы 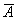 (вставить слово)
(вставить слово)
Пусть матрица 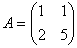 , тогда определитель матрицы, составленной из алгебраических дополнений матрицы А, равен:
, тогда определитель матрицы, составленной из алгебраических дополнений матрицы А, равен:
-3
-10
10
3
Общее решение системы линейных уравнений 
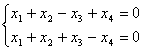 в векторной форме имеет вид:
в векторной форме имеет вид:
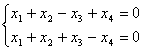 в векторной форме имеет вид:
в векторной форме имеет вид: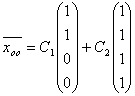
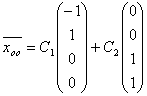
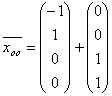
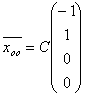
Общее решение системы 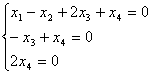 имеет вид:
имеет вид:
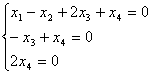 имеет вид:
имеет вид:система несовместима
система имеет единственное нулевое решение
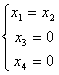 х2 свободная переменная
х2 свободная переменная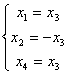 х3 свободная переменная
х3 свободная переменнаяОднородное уравнение с тремя переменными 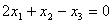 имеет решения в виде:
имеет решения в виде:
система имеет единственное решение 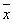 = (0, 0, 0)
= (0, 0, 0)
фундаментальная система решений состоит из одного вектора 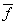 = (-1, 2, 0)
= (-1, 2, 0)
общее решение системы имеет вид 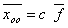 , где
, где 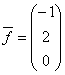
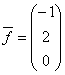
Дана матрица 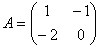 , вектор – столбец
, вектор – столбец 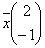 и вектор – строка
и вектор – строка 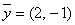 Укажите верные соответствия:
Укажите верные соответствия:
(4, - 2)
умножение невозможно
Система уравнений 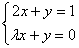 имеет единственное решение при значении
имеет единственное решение при значении 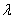 :
:
система имеет множество решений при любом 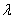
система несовместна при любом 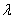
Дана система 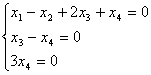 :
:
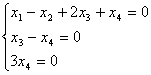 :
:размерность подпространства решений равна 1
разномерность подпространства решений равна
система имеет только нулевое решение
фундаментальная система решений содержит один вектор
Матрица 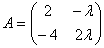 является вырожденной при
является вырожденной при 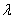 , равном:
, равном:
только при 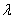 = 0
= 0
только при 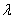 = 2
= 2
ни при каком значении 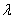
при всех 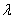
В системе уравнений 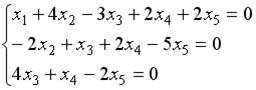 базисными (несвободными) переменными можно считать…
базисными (несвободными) переменными можно считать…
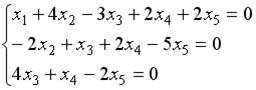 базисными (несвободными) переменными можно считать…
базисными (несвободными) переменными можно считать…Матрица В перестановочная с матрицей А и такая, что ее произведение с матрицей А дает единичную матрицу, называется _________ к матрице А (вставить слово)
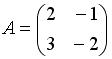 , имеет вид …
, имеет вид …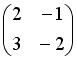
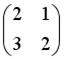
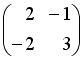
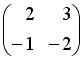
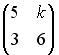 не имеет обратной при k, равном …
не имеет обратной при k, равном …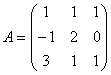 равен:
равен: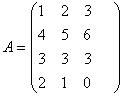 равен:
равен: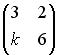 не имеет обратной при k, равном …
не имеет обратной при k, равном …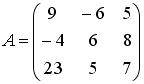 ,
,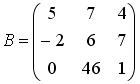
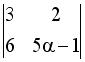 равен 0, если
равен 0, если 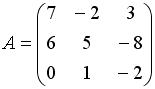 . Тогда алгебраическое дополнение элемента
. Тогда алгебраическое дополнение элемента 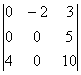 равен:
равен: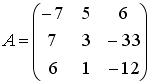 ,
,