Элементы теории функций и функциональный анализ
Укажите предложения, относящиеся к функции Грина задачи Штурма-Лиувилля :
эта функция отвечает собственному значению задачи Штурма -Лиувилля
эта функция является ядром интегрального оператора Фредгольма
эта функция определяет интегральный оператор Фредгольма, являющийся обратным к оператору Штурма-Лиувилля
эта функция существует и единственна тогда и только тогда, когда соответствующая однородная задача имеет только нулевое решение
Вполне непрерывный оператор отображает каждое ограниченное подмножество в _____________ (какое?)
Пусть 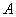 линейный оператор в линейном пространстве,
линейный оператор в линейном пространстве, 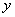 - заданный элемент. Установите соответствие между равенством и его названием
- заданный элемент. Установите соответствие между равенством и его названием
линейное однородное уравнение
линейное уравнение первого рода
линейное уравнение второго рода
Найдите норму линейного ограниченного оператора 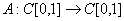 ,
, 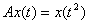 (укажите число)
(укажите число)
Скалярное произведение функций f(x) и g(x) в пространстве L2 [a,b] определяется по формуле: (f(x),g(x)) = 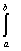 f(x)×g(x)dx.Тогда скалярное произведение элементов sinх и cosx в пространстве L2 [0,
f(x)×g(x)dx.Тогда скалярное произведение элементов sinх и cosx в пространстве L2 [0,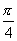 ] равно
] равно
0,5
0,2
0,25
0,45
Косинус угла между элементами f(x) и g(x) в пространстве L2 [a,b] определяется по формуле: cos(f(x),g(x)) = 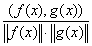 ; (f(x),g(x)) =
; (f(x),g(x)) = 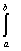 f(x)×g(x)dx ;
f(x)×g(x)dx ; 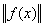 =
= 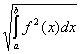 . Тогда косинус угла между элементами x и x3 в пространстве L2 [0,3] равен
. Тогда косинус угла между элементами x и x3 в пространстве L2 [0,3] равен
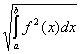 . Тогда косинус угла между элементами x и x3 в пространстве L2 [0,3] равен
. Тогда косинус угла между элементами x и x3 в пространстве L2 [0,3] равен-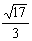
-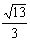
Уравнение 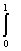
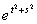 x(s)ds = 2t2 является интегральным уравнением Фредгольма _____ (какого?) рода (укажите порядок словом)
x(s)ds = 2t2 является интегральным уравнением Фредгольма _____ (какого?) рода (укажите порядок словом)
Укажите соответствие между интегральным уравнением и его видом
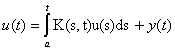
уравнение Абеля
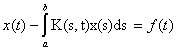
интегральное уравнение Фредгольма второго рода
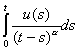 ,
, интегральное уравнение Вольтерра второго рода
Если j(х) является отображением отрезка [a,b] в себя и имеет непрерывную производную j¢(х) на отрезке [a,b], то коэффициент сжатия оценивается по формуле q = 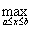 êj¢(х) ê. Тогда отображение j(х) = х3 отрезка [-0,5 ; 0,4] в себя является сжатым с коэффициентом сжатия _______ (укажите ответ в виде десятичной дроби)
êj¢(х) ê. Тогда отображение j(х) = х3 отрезка [-0,5 ; 0,4] в себя является сжатым с коэффициентом сжатия _______ (укажите ответ в виде десятичной дроби)
Норма элемента f(x) в пространстве 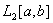 определяется по формуле:
определяется по формуле: 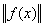 =
= 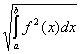 . Тогда норма элемента x
. Тогда норма элемента x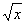 в пространстве
в пространстве 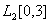 равна ___________ (укажите ответ в виде десятичной дроби)
равна ___________ (укажите ответ в виде десятичной дроби)
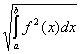 . Тогда норма элемента x
. Тогда норма элемента xПрименение алгоритма ортогонализации Грама-Шмидта к системе векторов u {2,1,3,-1}, v {7,4,3,-3} евклидова пространства R3 дает векторы u,w, причем вектор w равен
{3,2,-3,-1}
{1,1,1,1}
{-2,-1,-3,1}
{-7,-4,-3,3}
Скалярное произведение функций f(x) и g(x) в пространстве L2 [a,b] определяется по формуле: (f(x),g(x)) = 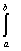 f(x)×g(x)dx. Тогда скалярное произведение элементов 3x2 и cosx3 в пространстве L2 [0,2] равно
f(x)×g(x)dx. Тогда скалярное произведение элементов 3x2 и cosx3 в пространстве L2 [0,2] равно
cos8
sin8
cos2
sin2
Точка х Î А называется предельной для подмножества В Í А, если любая e-окрестность точки х содержит точку множества В, отличную от точки х. Тогда множеством предельных точек множества решений неравенства ex + 3x2y4 > 1 является множество решений
ex + 3x2y4 £ 1
ex + 3x2y4 ³ 1
ex + 3x2y4 = 1
ex + 3x2y4 < 1
Неравенство Коши-Буняковского 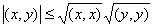 обращается в равенство, если векторы
обращается в равенство, если векторы 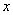 и
и 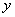
ортогональны
коллинеарны
являются базисными
линейно-независимы
Применение алгоритма ортогонализации Грама-Шмидта к системе векторов u {-1,0,-1}, v {1,-2,1} евклидова пространства R3 дает векторы u,w, причем вектор w равен
{0,-2,0}
{1,0,-1}
{2,0,1}
{-1,2,-1}
Рассмотрим пару систем 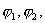 … и
… и 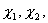 …элементов гильбертова пространства
…элементов гильбертова пространства  . Укажите условия, определяющие биортогональную систему:
. Укажите условия, определяющие биортогональную систему:
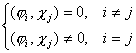
Косинус угла между элементами f(x) и g(x) в пространстве 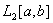 определяется по формуле: cos(f(x),g(x)) =
определяется по формуле: cos(f(x),g(x)) = 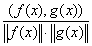 ; (f(x),g(x)) =
; (f(x),g(x)) = 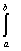 f(x)×g(x)dx ;
f(x)×g(x)dx ; 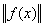 =
= 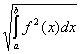 . Тогда косинус угла между элементами
. Тогда косинус угла между элементами 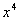 и 1 в пространстве
и 1 в пространстве 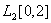 равен ______ (укажите ответ в виде десятичной дроби)
равен ______ (укажите ответ в виде десятичной дроби)
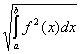 . Тогда косинус угла между элементами
. Тогда косинус угла между элементами Укажите условия, определяющие собственный вектор 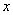 линейного оператора
линейного оператора 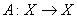 :
:
такой ненулевой вектор 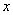 , что
, что 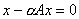 , где
, где 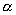 комплексное число
комплексное число
такой ненулевой вектор 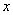 , что
, что 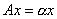 , где
, где 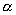 - комплексное число
- комплексное число
такой вектор 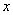 , что
, что 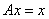
вектор, являющийся корнем уравнения 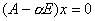 и
и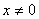 , для некоторого комплексного числа
, для некоторого комплексного числа 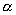
Норма оператора 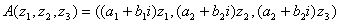 на унитарном пространстве С3 определяется по формуле
на унитарном пространстве С3 определяется по формуле 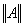 = max{
= max{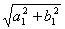 ,
,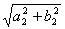 ,
,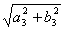 }. Тогда норма оператора
}. Тогда норма оператора 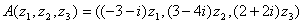 равна
равна
4
5
Наилучшее линейное приближение функции cosx в пространстве L2[-1,1] равно
sin1
cos1
2sin1
2cos1
Пусть 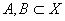 - замкнутые множества. Известно, что
- замкнутые множества. Известно, что 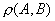 =0. Тогда возможны случаи:
=0. Тогда возможны случаи:
множества их предельных точек совпадают
одно множество содержит другое
дополнения этих множеств совпадают
их пересечение пусто
Установите соответствие между неравенством и его названием:
неравенство Минковского
неравенство Коши-Буняковского
неравенство Бесселя
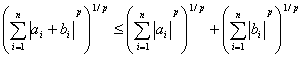
Подмножество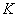 метрического пространства
метрического пространства  называется _________, если из каждой последовательности его элементов можно выделить фундаментальную подпоследовательность
называется _________, если из каждой последовательности его элементов можно выделить фундаментальную подпоследовательность
нормированным
компактным
банаховым
гильбертовым
Норма В интегрального оператора Фредгольма с ядром К(t,s) в пространстве L2[a,b] определяется по формуле В = 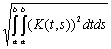 . Тогда норма интегрального оператора Фредгольма с ядром К(t,s) = (ts)6 в пространстве L2[0,1] равна _____ (укажите ответ в виде обыкновенной дроби)
. Тогда норма интегрального оператора Фредгольма с ядром К(t,s) = (ts)6 в пространстве L2[0,1] равна _____ (укажите ответ в виде обыкновенной дроби)
Пусть 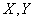 - линейные пространства. Тогда линейный оператор
- линейные пространства. Тогда линейный оператор 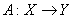 переводит линейно независимую систему
переводит линейно независимую систему 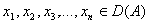 в ___________ (какую?)
в ___________ (какую?)
Укажите решение интегрального уравнения в пространстве непрерывных функций 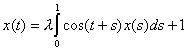
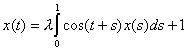
Скалярное произведение любых двух векторов ортогональной системы векторов равно _______ (укажите целое число)
Установите соответствие между названием пространства и его обозначением
пространство непрерывных функций с интегральной нормой
пространство непрерывных функций с равномерной нормой
пространство последовательностей
Точка х Î А называется предельной для подмножества В Í А, если любая e-окрестность точки х содержит точку множества В, отличную от точки х. Тогда множеством предельных точек множества {1;2;3;…} является
{1;2;3;…}
{0}
{0;1;-1;2;-2;…}
Æ - пустое множество
Линейный оператор 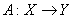 отображает каждое ограниченное подмножество в
отображает каждое ограниченное подмножество в  компактное подмножество
компактное подмножество 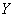 . Оператор
. Оператор 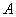 называется
называется
самосопряженным
непрерывным
вполне непрерывным
ограниченным
Укажите регулярные числа оператора А в евклидовом пространстве R2 A = 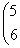
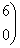 :
:
(-¥,9) È (-9,4) È (4,+ ¥)
(-¥,-4) È (-4,9) È (9,+ ¥)
(-¥;-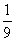 ) È (-
) È (-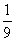 ; 0,25) È (0,25;+ ¥)
; 0,25) È (0,25;+ ¥)
(-¥;0,25) È (- 0,25; 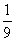 ) È (
) È (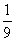 ;+ ¥)
;+ ¥)
Выберите вариант для верного утверждения : Расстояние от точки 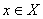 до множества
до множества 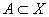 определяется равенством
определяется равенством 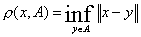 и _________ расстояния(ю) от этой точки до замыкания множества
и _________ расстояния(ю) от этой точки до замыкания множества 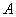
равно
не превосходит
больше
меньше
Расстоянием от точки 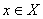 до множества
до множества 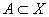 называется число
называется число 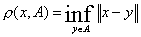 . Замыкание
. Замыкание 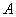 обозначается
обозначается 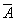 . Если
. Если 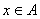 , то
, то
Уравнение 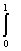 ( t6+s6)x(s)ds = sint является интегральным уравнением Фредгольма рода _____ (какого?) (укажите порядок словом)
( t6+s6)x(s)ds = sint является интегральным уравнением Фредгольма рода _____ (какого?) (укажите порядок словом)
В пространстве 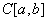 найдите решение интегрального уравнения
найдите решение интегрального уравнения 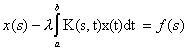 , если
, если 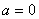 ,
, 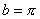 ,
, 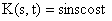 ,
, 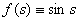 (укажите ответ алгебраических выражением)
(укажите ответ алгебраических выражением)
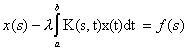 , если
, если Укажите, какие условия выполняются для интегрального оператора Фредгольма с ядром 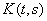 :
:
он неограничен
его норма не превосходит 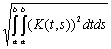
он вполне непрерывен
он непрерывен
Неравенство 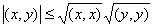 называют неравенством
называют неравенством
Коши-Буняковского
Бесселя
треугольника
Минковского
Применение алгоритма ортогонализации Грама-Шмидта к системе векторов u {-1,0,1}, v {5,4,-3} евклидова пространства R3 дает векторы u,w, причем вектор w равен
{4,1,1}
{1,4,1}
{1,1,4}
{1,4,4}
Известно, что расстояние от точки 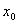 линейного нормированного пространства
линейного нормированного пространства  до гиперплоскости
до гиперплоскости 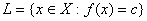 находится по формуле
находится по формуле 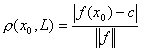 . Если
. Если 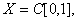
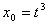 и
и 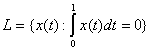 , то
, то 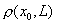 равно
равно
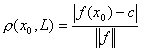 . Если
. Если 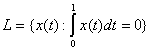 , то
, то 0
1/3
1/4
1
Точка х Î А называется предельной для подмножества В Í А, если любая e-окрестность точки х содержит точку множества В, отличную от точки х. Множеством предельных точек множества {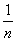 : n = 1;2;3;…} является
: n = 1;2;3;…} является
{0;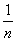 : n = 1;2;3;…}
: n = 1;2;3;…}
{0}
{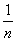 : n = 1;2;3;…}
: n = 1;2;3;…}
Æ - пустое множество
Укажите соответствие между интегральным уравнением и его видом
x(t) -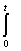 cos(t-s)x(s)ds = lnt
cos(t-s)x(s)ds = lnt
уравнение Фредгольма второго рода
уравнение Фредгольма первого рода
x(t) - 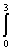
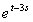 x(s)ds = et
x(s)ds = et
уравнение Вольтерра второго рода
Функция, сопоставляющая каждой паре элементов 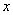 ,
,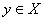 число
число 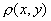 , обладающего следующими свойствами: a)
, обладающего следующими свойствами: a) 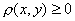 , причем
, причем 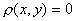
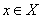 тогда и только тогда, когда
тогда и только тогда, когда 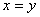 ; b)
; b) 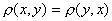 ; c)
; c) 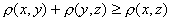 , называется _________ на множестве
, называется _________ на множестве  (ответ дайте одним словом)
(ответ дайте одним словом)
Коэффициент ряда Фурье элемента f(x) = x по ортогональной системе 1, coskx, sinkx, k = 1,2,… пространства L2[-p,p] при sinx равен
2
1
0
4
Имеем линейное нормированное пространство 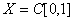 и определенный на
и определенный на 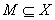 функционал
функционал 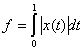 является
является
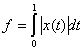 является
являетсяограниченным
вполне непрерывным
непрерывным
линейным
Вещественное линейное пространство, снабженное скалярным произведением, называется
банаховым
компактным
гильбертовым
евклидовым
Наилучшее линейное приближение функции 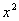 в пространстве
в пространстве 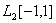 равно _______ (укажите ответ в виде обыкновенной дроби)
равно _______ (укажите ответ в виде обыкновенной дроби)
Целью процесса ортогонализации Грамма-Шмидта является построение
системы векторов, скалярное произведение любых двух векторов которой, равно нулю
системы линейно-независимых векторов
ортогонального базиса пространства
системы векторов с единичным модулем
Пусть 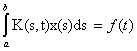 - интегральное уравнение Фредгольма первого рода,
- интегральное уравнение Фредгольма первого рода, 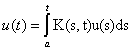 - интегральное уравнение Вольтерра первого рода,
- интегральное уравнение Вольтерра первого рода, 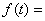
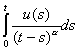 ,
, 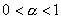 ,
, 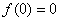 - уравнение Абеля. Укажите верные утверждения:
- уравнение Абеля. Укажите верные утверждения:
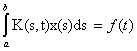 - интегральное уравнение Фредгольма первого рода,
- интегральное уравнение Фредгольма первого рода, 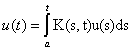 - интегральное уравнение Вольтерра первого рода,
- интегральное уравнение Вольтерра первого рода, 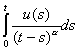 ,
, уравнение Абеля является частным случаем уравнений Фредгольма
уравнения Вольтерра являются частным случаем уравнений Фредгольма
уравнение Абеля является частным случаем уравнений Вольтерра
уравнения Фредгольма являются частным случаем уравнений Вольтерра
Функция, сопоставляющая каждой паре векторов 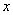 ,
,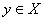 комплексное число
комплексное число 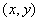 , обладающее следующими свойствами: a)
, обладающее следующими свойствами: a) 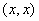 вещественно,
вещественно, 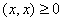 , причем
, причем 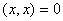 тогда и только тогда, когда
тогда и только тогда, когда 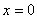 ; b)
; b) 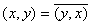 ; c)
; c) 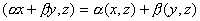 , для любых комплексных
, для любых комплексных 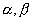 , называется
, называется
скалярным произведением на 
эрмитовым скалярным произведением на комплексном линейном пространстве 
метрикой на множестве 
нормой на множестве 
Найти норму функционала 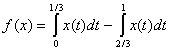 , определенного на пространстве
, определенного на пространстве 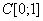 (укажите ответ в виде обыкновенной дроби)
(укажите ответ в виде обыкновенной дроби)
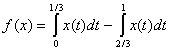 , определенного на пространстве
, определенного на пространстве