Теория вероятностей, математическая статистика и случайные процессы
Математическое ожидание функции Y = g(X) от непрерывной случайной величины Х вычисляется по формуле
MY =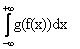 
MY =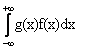 
MY =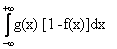
MY =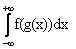
Игральный кубик бросают один раз. Вероятность того, что на верхней грани выпадет число очков, равное двум или четырем, равна
1/6
1/2
1/3
2/3
Вероятность того, что при бросании игрального кубика выпадет 0 очков , составляет …
0
1
По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию, равны 0,3 и 0,15. Тогда вероятность банкротства обоих предприятий равна
0,045
0,45
0,35
0,595
В урне лежит 2 белых и 3 черных шара. Последовательно, без возвращения и наудачу извлекают 3 шара. Тогда вероятность того, что первый и второй шары будут белыми, а третий шар - черный, равна …
Дискретная случайная величина Х имеет закон распределения вероятностей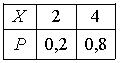 
. Математическое ожидание М(Х) этой случайной величины равно
. Математическое ожидание М(Х) этой случайной величины равно3,6
2,4
6
1
Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,5 и 0,4 соответственно. Тогда вероятность того, что в цель попадут оба стрелка, равна…
0,2
0,9
0,3
0,16
В урне находится 5 белых и 5 черных шаров. Из урны вынимаются четыре шара. Вероятность того, что два шара будут белыми, а два черными, равна …
Функция распределения случайной величины
не убывает
убывает
постоянна
не возрастает
Дискретная случайная величина Х задана законом распределения вероятностей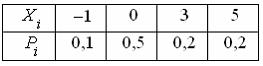 
Тогда значение интегральной функции распределения вероятностей 
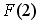равно …
Тогда значение интегральной функции распределения вероятностей равно …0,8
0,6
0,1
0,5
С первого станка на сборку поступает 60%, со второго – 40% всех деталей. Среди деталей первого станка 70% стандартных, второго – 80%. Взятая наудачу деталь оказалась стандартной. Тогда вероятность того, что она изготовлена на втором станке, равна …
Некий спортсмен выиграет чемпионат Европы с вероятностью 0,9; а чемпионат мира – с вероятностью 0,8. Вероятность выиграть оба чемпионата равна
0,8
0,72
0,85
1,7
Игральный кубик бросают один раз. Вероятность того, что на верхней грани выпадет число очков, меньшее чем два, равна
5/6
2/3
1/6
1/3
Вероятность того, что дом может сгореть в течение года, равна 0,01. Застраховано 400 домов. Для вычисления вероятности того, что сгорит больше 5 домов, следует использовать …
формулу Пуассона
таблицу плотности нормального распределения
локальную формулу Муавра-Лапласа
формулу полной вероятности
В первой урне 1 черный и 9 белых шаров. Во второй урне 4 белых и 6 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна…
0,65
0,25
0,7
0,13
В течение часа коммутатор получает в среднем 30 вызовов. Вероятность того, что на коммутатор не поступит ни одного вызова в течение часа, равна
e-30
30×e-30
1 – e-30
Устройство представляет собой параллельное соединение элементов S1, S2, S3;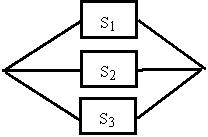 
каждый из них может выйти из строя с вероятностью 0,12. Функционирование схемы нарушается, если все они выходят из строя. Тогда вероятность правильной работы устройства равна…
каждый из них может выйти из строя с вероятностью 0,12. Функционирование схемы нарушается, если все они выходят из строя. Тогда вероятность правильной работы устройства равна…
0,123
В урне лежит 2 белых и 3 черных шара. Последовательно, без возвращения и наудачу извлекают 3 шара. Тогда вероятность того, что все они будут черными, равна …
Дисперсия произведения случайной величины Х и постоянной С равна
D(CX) =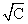 
DX
DXD(CX) = C×DX
D(CX) = |C| ×DX
D(CX) = C2DX
Вероятность появления события А в 20 независимых испытаниях, проводимых по схеме Бернулли, равна 0,7. Тогда дисперсия числа появлений этого события равна
14
0,35
0,42
4,2
Вероятность того, что студент сдаст экзамен, равна 0,8. Тогда вероятность того, что студент сдаст хотя бы один из 3 экзаменов сессии, равна …
0,008
0,992
0,128
0,333
Дискретная случайная величина Х имеет закон распределения вероятностей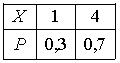 
. Математическое ожидание М(Х) этой случайной величины равно
. Математическое ожидание М(Х) этой случайной величины равно1,3
3,1
1
5
Дискретная случайная величина Х имеет закон распределения вероятностей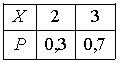 
. Математическое ожидание М(Х) этой случайной величины равно
. Математическое ожидание М(Х) этой случайной величины равно2,3
2,7
5
1
Вероятность появления события А в 20 независимых испытаниях, проводимых по схеме Бернулли, равна 0,2. Тогда дисперсия числа появлений этого события равна
0,32
3,2
4
0,01
В урне 4 билета. Из них 2 выигрышных. Вынимаем три билета случайным образом. Р3 – вероятность вынуть три выигрышных билета. Р2 – вероятность вынуть два выигрышных билета. Р1 – вероятность вынуть один выигрышный билет. Р0 – вероятность, что все билеты не выиграли. Выберите верные утверждения
Р1 = 0,4
Р0 = 0,1
Р3 = 0
Р2 = 0,5
Вероятность достоверного события равна
0,75
любому числу
1
0,5
В квадрат со стороной 3 брошена точка. 
Тогда вероятность того, что она попадет в выделенную область, равна …
Тогда вероятность того, что она попадет в выделенную область, равна …
Вероятность стрелку попасть в мишень равна 0,9. Стрелок стреляет два раза. Р0 – вероятность, что попаданий нет. Р1 – вероятность, что попал один раз Р2 – вероятность двух попаданий.
Р1
0,81
Р0
0,01
Р2
0,18
Выпущено 500 лотерейных билетов. 40 с выигрышем по 1 руб., 10 – по 5 руб., 5 – по 10 руб. Вам подарили 1 билет. Найдите математическое ожидание выигрыша. Ответ дайте десятичной дробью
В урне 5 билетов. Из них 2 выигрышных. Вынимаем три билета случайным образом. Р3 – вероятность вынуть три выигрышных билета. Р2 – вероятность вынуть два выигрышных билета. Р1 – вероятность вынуть один выигрышный билет. Р0 – вероятность, что все билеты не выиграли. Выберите верные утверждения
Р2 = 0,3
Р3 = 0,1
Р1 = 0,2
Р0 = 0,1
Игральный кубик бросают один раз. Вероятность того, что на верхней грани выпадет число очков, кратное четырем, равна
5/6
1/6
0
1/2
Вероятность того, что при бросании одного игрального кубика выпадет число очков, кратное четырем, составляет …
4
Два стрелка стреляют по мишени. Вероятность попадания в цель у одного стрелка 0,7, у другого – 0,8. Найти вероятность того, что цель будет пора жена Ответ дайте десятичной дробью
Для математического ожидания произведения случайной величины Х и постоянной С справедливо свойство
М(СХ) = C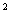
МХ
МХМ(СХ) = С×МХ
М(СХ) = |C| МХ
М(СХ) =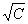 
×MX
×MXДва стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,7 и 0,2 соответственно. Тогда вероятность того, что в цель попадут оба стрелка, равна…
0,14
0,24
0,9
0,12
Вероятность появления события А в 10 независимых испытаниях, проводимых по схеме Бернулли, равна 0,6. Тогда дисперсия числа появлений этого события равна
2,4
0,24
0,06
6
Игральный кубик бросают один раз. Вероятность того, что на верхней грани выпадет число очков, равное трем или четырем, равна
1/2
1/6
2/3
1/3
Из урны, в которой находятся 5 белых и 7 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна…
1
Вероятность стрелку попасть в мишень равна 0,9. Стрелок стреляет пять раз. Р1 – вероятность попасть точно один раз. Р2 – вероятность попасть точно два раза. Р3 – вероятность попасть точно три раза
Р1
0,0729
Р2
0,0081
Р3
0,00045
В тире лежат два ружья. Вероятность стрелку попасть из первого ружья 0,8. Вероятность стрелку попасть из второго ружья 0,6. Стрелок заходит в тир, наугад берёт ружьё, два раза стреляет. Р0 – вероятность, что попаданий нет. Р1 – вероятность, что попал один раз. Р2 – вероятность двух попаданий
Р1
0,5
Р0
0,1
Р2
0,4
В урне 5 билетов. Из них 2 выигрышных. Вынимаем три билета случайным образом. Р3 – вероятность вынуть три выигрышных билета. Р2 – вероятность вынуть два выигрышных билета. Р1 – вероятность вынуть один выигрышный билет. Р0 – вероятность, что все билеты не выиграли. Выберите верные утверждения
Р1 = 0,6
Р3 = 0
Р2 = 0,2
Р0 = 0,2
Среднеквадратическое отклонение определяется как
В физкультурной группе 11 спортсменов и среди них 6 перворазрядников. Вероятность того, что среди двух случайно выбранных спортсменов окажется два перворазрядника, равна
0,11
Укажите соответствие между формулами и их значениями
n
Непрерывная случайная величина X задана плотностью распределения вероятностей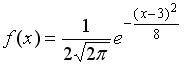 
.Тогда математическое ожидание этой нормально распределённой случайной величины равно …
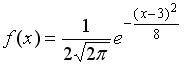.Тогда математическое ожидание этой нормально распределённой случайной величины равно …3
4
2
8
Студенту предлагают 6 вопросов и 4 ответа на каждый вопрос, из кото рых он должен указать тот, который ему кажется правильным. Студент не под готовился и отвечает наугад. Какова вероятность того, что он правильно ответит ровно на 3 вопроса? Ответ дайте десятичной дробью (с точностью до трех знаков после запятой)
Стрелок попадает в цель с вероятностью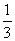 
. Стрелок стреляет три раза. Р3 – вероятность попасть три раза. Р2 – вероятность попасть два раза, один раз смазать. Р1 – вероятность попасть один раз, два раза смазать. Р0 – вероятность все три раза смазать. Выберите верные утверждения
. Стрелок стреляет три раза. Р3 – вероятность попасть три раза. Р2 – вероятность попасть два раза, один раз смазать. Р1 – вероятность попасть один раз, два раза смазать. Р0 – вероятность все три раза смазать. Выберите верные утвержденияР0 =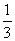
Р1 =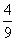 
Р3 =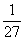 
Р2 =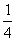 
Вероятность наступления некоторого события не может быть равна
2,3
0
0,7
0,5
На тестировании студент выбирает наугад один ответ из 4 возможных, среди которых один ответ верный. Вероятность того, что он правильно ответит хотя бы на один вопрос из двух предложенных, равна
1 –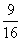 
×Вероятность достоверного события равна
0
1
0,999
– 1