Алгебра и геометрия (курс 1)
Поверхность, заданная каноническим уравнением 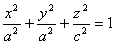 , называется _____________.
, называется _____________.
Уравнения асимптот гиперболы 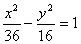 имеют вид:
имеют вид:
2х + 3у = 0 и 2х – 3у = 0
36х + 16у = 0 и 36х – 16у = 0
х + 4у = 0 и х – 4у = 0
6х + у = 0 и 6х – у = 0
Направляющий вектор прямой 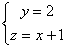 равен:
равен:
s̅={1,0,-1}
s̅={1,0,1}
s̅={0,1,0}
s̅={1,2,-1}
Координаты фокусов гиперболы 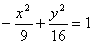 равны
равны
F1(0, -5); F2(0, 5)
F1(0, -3); F2(0, 3)
F1(-5, 0); F2(5, 0)
F1(0, -4); F2(0, 4)
Укажите верные соответствия для матрицы 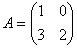 ,
, 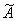 – присоединенная.
– присоединенная.
A2 =
A-1 =
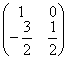
à =
Скалярное произведение векторов a̅=(1,1,1,1), b̅=(2,0,-2,1) равно:
1
9
4
3
Для матрицы 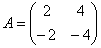 собственными числами являются:
собственными числами являются:
λ1 = 0, λ2 = -2
λ1 = -2, λ2 = -1
λ1 = λ2 = -2
λ1 = 0, λ2 = 2
Прямая 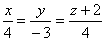 пересекает поверхность
пересекает поверхность 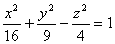 в точке:
в точке:
М(4, 3, -2)
М(4, -3, 2)
М(-4, 3, 2)
М(4, 3, 2)
Две прямые 3x – y – 18 = 0 и x - 2y – 6 = 0 пересекаются
в точке M (6, 0)
под углом φ=π/2
под углом φ=π/4
под углом φ=π/6
Сумма произведений элементов аij i-ой строки квадратной матрицы А на их алгебраические дополнения равна ______________ матрицы.
Даны матрицы 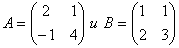 , тогда определитель произведения матриц det (ATBT) равен:
, тогда определитель произведения матриц det (ATBT) равен:
1 / 9
9
1 / 7
7
Результат выполнения действий в выражении (2i – i2)2
тригонометрическая форма результата имеет вид: 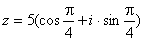
модуль результата: |z| = 5
в алгебраической форме имеет вид: z = -3 + 4i
аргумент результата: φ = π
Система векторов a̅1,a̅2,…,a̅k называется линейно _____________________, если никакая нетривиальная линейная комбинация этих векторов не равна нуль - вектору.
Система 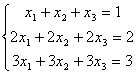 имеет:
имеет:
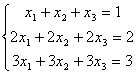 имеет:
имеет:единственное решение
множество решений
лишь три решения
лишь два решения
Установите верные соответствия. Составляют ли системы многочленов базис в пространстве многочленов степени не выше двух:
не составляют, т.к. система линейно зависима
не составляет, т.к. система не принадлежит пространству
составляет базис
Квадратичная форма неотрицательно определена, если она принимает ______________ значения для любого вектора x̅.
Эллипс 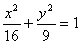 является ___________________ сечением однополостного гиперболоида
является ___________________ сечением однополостного гиперболоида 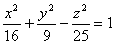 .
.
Эллипсоид 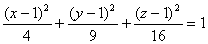 :
:
является поверхностью вращения
имеет полуоси а = 2, в = 3, с = 4
проходит через точку М(1, 1, 1)
имеет оси симметрии х = 1, у = 1, z = 1
Укажите верные соответствия для данной матрицы 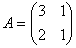 , Ã – матрица, составленная из алгебраических дополнений матрицы А.
, Ã – матрица, составленная из алгебраических дополнений матрицы А.
det (3A ÃT) =
1
det 2A =
4
det A =
9
Укажите верные соответствия между плоскостями и кривыми, по которым эти плоскости пересекают конус x2 - y2 + z2 = 0.
x = 0
по гиперболе -x2 + y2 = 1
y = 3
по окружности x2 + z2 = 9
z = 1
по двум прямым y = z и y = –z
Указать верные соответствия между данными векторами x̅ и y̅ и углами между ними.
x̅=(2,2,2,0,-2), y̅=(3,3,3,0,0)
φ = π/2
x̅=(1,1,1,1), y̅=(1,0,1,0)
φ = π/4
x̅=(2,1,3,2,), y̅=(1,2,-2,1)
φ = π/6
В пространстве многочленов степени n ≤ 2 задан оператор дифференцирования 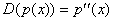 . Его матрица в базисе
. Его матрица в базисе 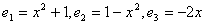 равна:
равна:

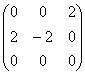
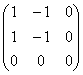

Прямая 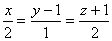 пересекает плоскость
пересекает плоскость 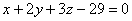 в точке:
в точке:
М(0, 1, -1)
М(6, 4, 5)
М(2, 1, 2)
М(1, 2, 3)
Свободными переменными в системе уравнений 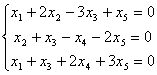 являются:
являются:
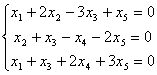 являются:
являются:x5
x1, x2
x2, x3
x4, x5
Дана система уравнений 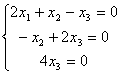 , тогда:
, тогда:
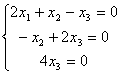 , тогда:
, тогда:система имеет лишь тривиальное решение x̅=0
dim V = 1, V – подпространство решений
det A-1 = 0
det A = -8
Плоскость z + 1 = 0 пересекает однополостный гиперболоид 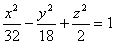 по гиперболе с полуосями, равными:
по гиперболе с полуосями, равными:
4 и 3
Пусть det A = 6, det B = 2, тогда:
det (AB) = 12
det (AB-1) = 3
det (AA-1) = 1 / 6
det (ATBT) = 1 / 12
Общее уравнение прямой, проходящей через точку А(-1, 3) параллельно вектору 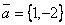 , имеет вид:
, имеет вид:
В пространстве многочленов степени n ≤ 2 задан оператор 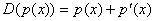 и многочлен
и многочлен 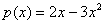 . Координаты образа D(p(x)) по базису
. Координаты образа D(p(x)) по базису 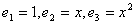 равны:
равны:
(2, 4, -3)
(2, -4, -3)
(2, -6, -3)
(-3, -4, 2)
Собственными векторами матрицы 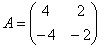 являются вектора:
являются вектора:
(-1, -1)
(0, 0)
(1, -1), (1, 2)
(1, -2), (-1, 1)
Общее уравнение плоскости, проходящей через ось OX и точку М0(0, -2, 3), имеет вид:
Вектор а̅ – собственный вектор матрицы А, соответствующий собственному значению λ. Тогда для матрицы А2 справедливо утверждение:
а̅ – не является собственным для А2
а̅ – собственный для А2, соответствует собственному значению 2λ
а̅ – собственный для А2, соответствует собственному числу 2λ2
а̅ – собственный для А2, соответствует собственному значению λ2
Уравнение 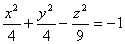 является каноническим уравнением двухполостного ____________ вращения
является каноническим уравнением двухполостного ____________ вращения
Нормированным базисом из собственных векторов матрицы 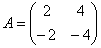 являются вектора:
являются вектора:
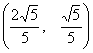
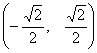
(–2, 1) (1, –1)
(1, –1) (2, –1)
Для матрицы 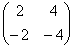 вектор x̅ = (1, -1) является собственным, отвечающим собственному значению:
вектор x̅ = (1, -1) является собственным, отвечающим собственному значению:
λ = -2
λ = 1
λ = 2
λ = -1
Даны векторы a̅={-1,0,1}, b̅={2,1,2}и c̅={-1,0,3}. Указать верные соответствия:
векторы a̅, b̅, c̅
ортогональны
вектор d̅=[a̅×c̅] и орт j̅
коллинеарны
векторы a̅, b̅
компланарны
Квадратичная форма 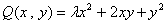 отрицательно определена при λ:
отрицательно определена при λ:
ни при каких λ
λ > 1/2
λ < 2
0 ≤ λ ≤ 1/2
Число Δ=(a11a22 – a21a12) называется _______________ квадратной матрицы второго порядка 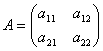 .
.
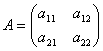 .
.Собственному значению λ = 3 матрицы 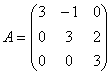 отвечает:
отвечает:
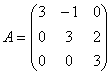 отвечает:
отвечает:подпространство собственных векторов размерности 3
только один собственный вектор
собственных векторов, отвечающих λ = 3, нет
подпространство собственных векторов размерности 1
Уравнения асимптот гиперболы 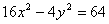 имеют вид:
имеют вид:
y = ± 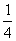 x
x
y = ± 2x
y = ± 4x
y = ± 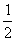 x
x
Уравнение 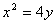 в пространстве определяет:
в пространстве определяет:
эллиптический цилиндр с образующими, параллельными оси OZ
эллиптический параболоид
параболический цилиндр с образующими, параллельными оси OZ
две плоскости 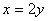 и
и 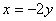
Укажите верные соответствия между уравнением прямой на плоскости и типом этого уравнения:
y = kx + b
уравнение прямой, проходящей через две заданные точки
Ax + By + C = 0
общее уравнение прямой
(x – x1)/(x2 – x1) = (y – y1)/(y2 – y1)
уравнение прямой с угловым коэффициентом
Действительный корень характеристического уравнения матрицы А является ________________ матрицы
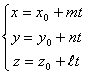 называются _______________ уравнениями прямой.
называются _______________ уравнениями прямой.