Математический анализ (курс 3)
Длина дуги кривой 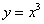 с концами в точках О(0, 0) и А(3, 27) вычисляется с помощью интеграла
с концами в точках О(0, 0) и А(3, 27) вычисляется с помощью интеграла
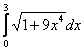
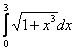
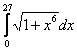
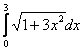
Коэффициент А(l) в задаче Коши для уравнения теплопроводности Ut = Uxx, U(x,0) = j(x) вычисляется по формуле А(l) = 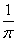
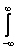 j(x)cosx
j(x)cosx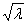 dx Тогда коэффициент А(l) при U(x,0) = j(x) =
dx Тогда коэффициент А(l) при U(x,0) = j(x) = 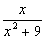 равен
равен
0
1
Ряд Фурье функции f(x) = |х| (-1 < x < 1), Т = 2 в точке х0 = 1 сходится к значению
1
-1
2
расходится в точке х0 = 1
Теорема существования и единственности решения задачи Коши для дифференциального уравнения 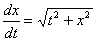 выполнена в области
выполнена в области
{x > -1, -¥ < t < +¥}
{t > -1, -¥ < x < +¥}
{-¥ < t, x < +¥}
{t2 + x2 > 0}
Необходимым условием экстремума функции 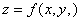 в точке
в точке 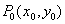 является
является
равенство нулю частных производных 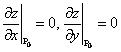 , если они существуют в точке
, если они существуют в точке 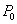
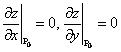 , если они существуют в точке
, если они существуют в точке то, что 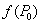 больше или меньше всех значений функции
больше или меньше всех значений функции
условие 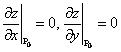
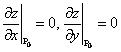
то, что производная в этой точке равна нулю
Функция u0(x,y,z) = 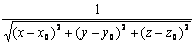 является фундаментальным решением уравнения
является фундаментальным решением уравнения
Волнового
Лапласа
Теплопроводности
Пуассона
Интегральное уравнение Фредгольма x(t) - l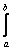 K(t,s)x(s)ds = y(t) c параметром l решается методом последовательных приближений при <
K(t,s)x(s)ds = y(t) c параметром l решается методом последовательных приближений при < 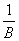 , где В =
, где В = 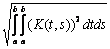 . Тогда интегральное уравнение Фредгольма x(t) - l
. Тогда интегральное уравнение Фредгольма x(t) - l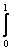 t4s5x(s)ds = y(t) решается методом последовательных приближений при l, меньшем
t4s5x(s)ds = y(t) решается методом последовательных приближений при l, меньшем
2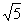
3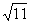
5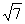
2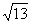
n-й частичной суммой ряда называется
сумма первых n членов ряда
общий член ряда
сумма первых двух членов ряда
сумма первых трех членов ряда
Если функция 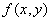 непрерывна в замкнутой ограниченной области
непрерывна в замкнутой ограниченной области 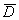 , дифференцируема во внутренних точках D и имеет в D единственный экстремум - максимум, то своего наименьшего значения она достигает
, дифференцируема во внутренних точках D и имеет в D единственный экстремум - максимум, то своего наименьшего значения она достигает
во внутренней или граничной точке
в любой точке
в другой точке внутри D
в граничной точке области
Уравнение теплопроводности в пространстве имеет вид
Ux = a2(Uxx + Uyy)
Utt = a2(Uxx +Uyy + Uzz)
Ut = a2(Uxx +Uyy + Uzz)
U = a2(Uxx +Uyy + Uzz)
Функция у = sin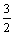 x является решением краевой задачи
x является решением краевой задачи
y¢¢ + 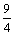 y = 0, y¢(0) = y(2p) = 0
y = 0, y¢(0) = y(2p) = 0
y¢¢ + 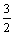 y = 0, y(0) = y(2p) = 0
y = 0, y(0) = y(2p) = 0
y¢¢ + 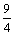 y = 0, y(0) = y(2p) = 0
y = 0, y(0) = y(2p) = 0
y¢¢ + 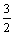 y = 0, y¢(0) = y(2p) = 0
y = 0, y¢(0) = y(2p) = 0
Средней кривизной кривой 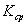 (плоской или пространственной) на участке между ее точками
(плоской или пространственной) на участке между ее точками 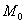 и
и 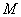 называется
называется
абсолютная величина отношения угла между касательными прямыми в точках 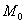 и
и 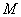 к длине дуги
к длине дуги 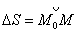
угол между касательными в 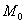 и
и 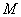
отношение угла между касательными в точках 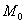 и
и 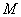 к
к 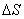
абсолютная величина угла между касательными прямыми в точках 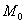 и
и 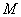
У графика функции 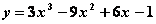
точки перегиба нет
функция возрастает
точка перегиба есть - это 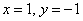
критических точек для 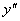 нет
нет
Последовательность 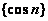 является
является
бесконечно большой
бесконечно малой
ограниченной
неограниченной
Функция у = cos3pх является собственной функцией задачи Штурма-Лиувилля у¢¢ + lу = 0, у¢(0) = у¢(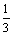 ) = 0 с собственным значением
) = 0 с собственным значением
= 3p
= 9p2
= 3
= 9
Фундаментальным решением уравнения Лапласа в пространстве называется функция
u0 = ln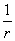 ;
;
u0 = 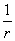 ;
;
u0 = r ;
u0 = 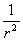 ;
;
Ряд Фурье функции f(x) = |х| (- p < x £ p), Т = 2p, в точке х = 0 сходится к значению
1
0
2p
Если 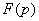 - изображение функции-оригинала
- изображение функции-оригинала 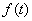 , то изображением интеграла
, то изображением интеграла 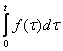 является
является
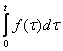 является
является
Регулярные числа оператора А в евклидовом пространстве R2 A = 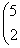
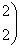 :
:
(-¥,1) È (1,6) È (6,+ ¥)
(-¥,-1) È (-1,-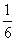 ) È (-
) È (-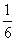 ,+ ¥)
,+ ¥)
(-¥,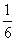 ) È (
) È (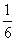 ,1) È (1,+ ¥)
,1) È (1,+ ¥)
(-¥,-6) È (-6,-1) È (-1,+ ¥)
Функция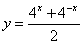 является
является
нечетной, непериодической
четной, непериодической
нечетной, имеет период Т = 0
четной, имеет период Т = 0
Гиперболический тип имеет уравнение
3Uxx + 2Uxy + Uyy = 0
3Uxy + 4Uyy = 0
3Uxx + 4Uyy = 0
Uxx + 2Uxy + Uyy = 0
Функции U1 = 2xy + 5x - 3y и U2 = 5(x2 - y2) являются решениями уравнения
Uyy + U = 0
Uxx + Uyy = 0
Ux + Uyy = 0
Uxx - Uyy = 0
Общее геометрическое содержание теорем Ролля, Лагранжа, Коши:
касательная в некоторой точке кривой параллельна оси Ox
касательная всегда параллельна хорде
между двумя корнями функции лежит корень производной
на кривой найдется точка, в которой касательная параллельна хорде, стягивающей концы кривой
Точка х Î А называется предельной для подмножества В Í А, если любая e-окрестность точки х содержит точку множества В, отличную от точки х. Тогда множеством предельных точек множества (-1,+¥) является
(-1,+ ¥)
[-1,+ ¥)
(-¥,-1]
[-1,+ ¥]
Расстояние от f(x) до g(x) в пространстве С [a,b] определяется по формуле: r(f(x),g(x)) = 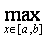
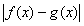 Тогда расстояние между х3 + 3х2 + 1 и 24х в С [0,3] равно
Тогда расстояние между х3 + 3х2 + 1 и 24х в С [0,3] равно
17
27
15
35
Для функции 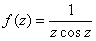 точка
точка 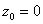
изолированной особой точкой не является
является полюсом
является существенно особой точкой
является устранимой особой точкой
Точка 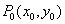 является точкой максимума функции
является точкой максимума функции 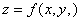 , если
, если
значение 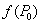 больше всех значений функции
больше всех значений функции 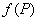
найдется такая 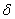 -окрестность
-окрестность 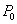 , что значение
, что значение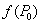 больше любого значения
больше любого значения 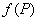 , принятого в этой окрестности
, принятого в этой окрестности
найдется такой интервал, содержащий 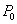 , что значение
, что значение 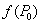 больше любого значения
больше любого значения 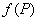 , принятого в этом интервале
, принятого в этом интервале
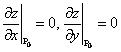
Функция 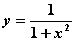 имеет интервалов монотонности -
имеет интервалов монотонности -
три
нет интервалов монотонности
один
два
промежуточный аргумент
функция от x
производная сложной функции
сложная функция от x; функция от функции; суперпозиция функций 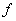 и
и 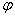
Дифференциальное уравнение 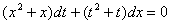 является
является
однородным уравнением первого порядка
уравнением с разделенными переменными
уравнением Бернулли
уравнением с разделяющимися переменными
Функция f(x) = x разлагается в ряд Фурье 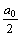 +
+ 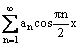 на отрезке [0, 2]. Коэффициент a0 равен
на отрезке [0, 2]. Коэффициент a0 равен
p
1
2
Если 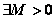
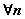
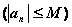 , то
, то 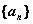 последовательность
последовательность
ограниченная
неограниченная
бесконечно большая
бесконечно малая
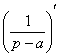 является
является