Теория вероятностей и математическая статистика (курс 2)
Случайная величина (Х,Y) распределена по двумерному нормальному закону, параметры которого равны: ax=1; ay=2; r=0,5; sx=1; sy=2. Уравнение регрессии X на Y имеет вид
x-1=y-2
x-1=0,5(y-2)
x=0,25y+0,5
x=0,5(y-2)
Дисперсия произведения случайной величины Х и постоянной С равна
D(CX) = C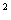 DX
DX
D(CX) = |C| DX
D(CX) = 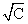 DX
DX
D(CX) = C DX
DX
Математическое ожидание и среднеквадратическое отклонение случайной величины Х, распределенной по нормальному закону, равны соответственно 30 и 10. Плотность распределения Х имеет вид
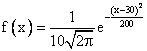
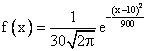
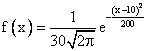
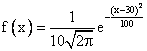
Величина x имеет распределение N(a, s). Вероятность p{|x - a| < 2s} равна
0,977
0,997
0,954
0,023
Переходные матрицы цепи Маркова обладают следующими свойствами:
все их элементы отличны от нуля, а их сумма ограничена
все их элементы неотрицательны и их суммы по строкам равны 1
все их элементы положительны
суммы по строкам матрицы не превосходят 1
Для выборки объема n = 9 сосчитали выборочную дисперсию S2 = 3.86. Исправленная дисперсия равна
4.50
4.34
4.20
4.45
Формула 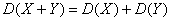
всегда верна
неверна
верна для независимых 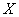 и
и 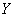
верна для зависимых 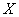 и
и 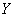
Простейший поток является
биномиальным
потоком Бернулли
пуассоновским
гауссовским
Для того, чтобы построить 95%-ый доверительный интервал для математического ожидания m случайной величины, распределенной нормально с известной дисперсией s2, по выборке объема n вычисляется 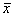 и используется следующая формула:
и используется следующая формула:
Производится выборка объема n = 100 из генеральной совокупности, имеющей распределение N(20,4). По выборке строится выборочное среднее 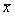 . Эта случайная величина имеет распределение
. Эта случайная величина имеет распределение
N(20; 4)
N(20; 0,04)
N(20; 0,4)
N(0,2; 0,04)
Для проверки гипотезы Н0 , состоящей в том, что s21=s22, на уровне значимости a используется статистика F,
вычисляются несмещенные оценки дисперсий s21 и s22 и статистика 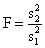
вычисляются оценки дисперсий S21 и S22 и статистика 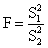
вычисляются оценки дисперсий S21 и S22 и статистика 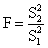
вычисляются несмещенные оценки дисперсий s21 и s22 и статистика 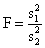
Функция распределения случайной величины
не возрастает
постоянна
не убывает
убывает
Случайная величина 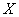 имеет математическое ожидание
имеет математическое ожидание 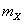 и дисперсию
и дисперсию 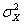 . Тогда вероятность того, что величина
. Тогда вероятность того, что величина 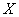 отклонится от своего математического ожидания не менее чем на
отклонится от своего математического ожидания не менее чем на 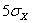 ,
, 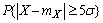 имеет оценку сверху
имеет оценку сверху
0,2
0,04
0,5
0,25
Случайная величина Х называется центрированной, если
DX = MX
DX = 1
МХ = 0
MX = 1
В итоге четырех измерений некоторой физической величины одним прибором получены следующие результаты: 8, 9, 11, 12. Выборочная средняя результатов измерений, выборочная и исправленная дисперсии ошибок прибора составляют соответственно
9; 25; 5
10; 25; 5
9; 2,5; 3,(3)
10; 2,5; 3,(3)
Если каждый элемент выборки объема n: х1, х2, …, хn увеличить на 5 единиц, то
выборочное среднее 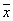 не изменится, а выборочная дисперсия S2 увеличится на 5
не изменится, а выборочная дисперсия S2 увеличится на 5
выборочное среднее 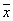 увеличится на 5, а выборочная дисперсия S2 увеличится на 25
увеличится на 5, а выборочная дисперсия S2 увеличится на 25
выборочное среднее 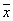 увеличится на 5, а выборочная дисперсия S2 не изменится
увеличится на 5, а выборочная дисперсия S2 не изменится
выборочное среднее 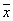 увеличится на 5, а выборочная дисперсия S2 увеличится тоже на 5
увеличится на 5, а выборочная дисперсия S2 увеличится тоже на 5
Случайный процесс X(t) = Vt + 5, где V(t) - случайная величина, имеющая стандартно нормальное распределение, f(x, t) - плотность распределения сечения этого процесса имеет вид
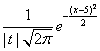
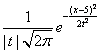
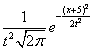
Вероятность для случайной величины X , распределенной «нормально с параметрами 0,1» - N[0,1], попасть внутрь интервала [-3,3] равна
0.9973
0.95
0.8
0.68
На первой полке12 книг, из которых 4 на русском языке, на второй полке 10 книг, из которых 5 на русском языке. С каждой полки выбирается по одной книге. Вероятность того, что хотя бы одна из книг будет на русском языке, равна
0,60
0,30
xi - независимые, нормально распределённые, стандартные N(0,1) случайные величины. Распределение вероятностей, которое имеет случайная величина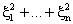 , называется
, называется
распределением Фишера-Снедекора
N(0,1)
распределением Стьюдента
распределением хи-квадрат с n степенями свободы (χ2n)
Если каждый элемент выборки объема n: х1, х2, …, хn увеличить в 5 раз, то выборочное среднее 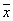
возрастет в 5 раз, а выборочная дисперсия S2 увеличится в 25 раз
возрастет в 25 раз, а выборочная дисперсия S2 увеличится в 5 раз
возрастет в 5 раз, а выборочная дисперсия не изменится
возрастет в 5 раз и выборочная дисперсия S2 возрастет в 5 раз
Относительная пропускная способность одноканальной системы с ограниченной очередью длиной m, интенсивностью потока заявок l, интенсивностью потока обслуживания m, загрузкой системы r и вероятностью p0 - того, что система свободна, и r - среднее число заявок в очереди, равна:
a = rm+1p0
a = 1 -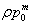
a = 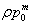
a = 1 - rm+1p0
В многоканальной системе массового обслуживания n каналов, длина очереди ограничена величиной m; загрузка системы - r; вероятность того, что система свободна, - p0; l и m соответственно интенсивности потока заявок и потока обслуживания. Размеченный граф состояний системы имеет вид
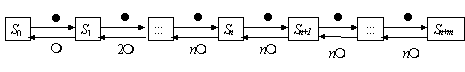



Вероятности 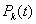 состояний
состояний 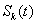 марковского случайного процесса - это
марковского случайного процесса - это
Абсолютная пропускная способность системы с отказами и n каналами, интенсивностью потока заявок l, интенсивностью потока обслуживания m, загрузкой системы r, средним числом заявок в очереди r и вероятностью того, что система свободна p0, равна
Из урны, в которой находятся 5 белых, 4 зеленых и 3 красных шара, наугад извлекается один шар. Вероятность того, что он будет цветным, равна
0,5
1
Оценка интенсивности входящего потока для одного наблюдения одноканальной системы с неограниченной очередью, t0 - общее время, когда система свободна, u - число обслуженных требований, а u - число требований, поступивших в систему за время наблюдения t; равна
Для случайного процесса X(t) с непрерывным временем его дисперсия есть
неотрицательная числовая функция
непрерывная функция
постоянная функция
случайная величина
Случайный процесс с дискретным временем - это семейство случайных величин 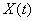
где 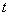 принимает конечное число значений
принимает конечное число значений
где 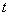 принимает дискретные значения
принимает дискретные значения
представляющих собой набор случайных чисел
которые принимают только дискретные значения
Наблюдения проводятся над системой (X : Y) двух случайных величин. Выборка состоит из пар чисел: (х1: y1), (х2: y2), …, (хn : yn). Найдены 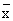 , S
, S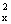 для хi и
для хi и 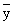 , S
, S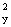 для yi (
для yi (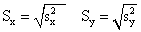 ). Тогда выборочный коэффициент корреляции rxy находится по формуле
). Тогда выборочный коэффициент корреляции rxy находится по формуле
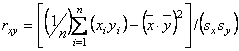
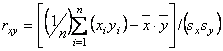
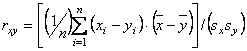
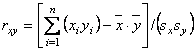
Математическое ожидание непрерывной случайной величины - это
Оценка интенсивности потока обслуживания для наблюдения в течение времени t над n-канальной системой с очередью длины m; u - число обслуженных заявок, cn - суммарное время, затраченное на обслуживание всех u заявок; равна
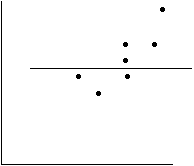
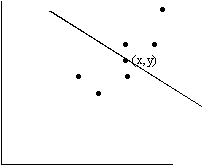
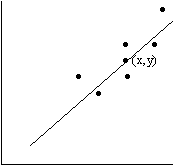
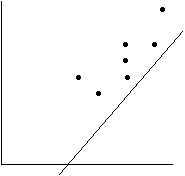
График прямой, построенной для обработки наблюдений методом наименьших квадратов, имеет вид
Случайная величина Х распределена равномерно на 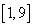 , тогда вероятность попасть в интервал
, тогда вероятность попасть в интервал 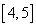 равна
равна
Выборочная дисперсия выборки объема n=9 равна S2=3,86 , исправленная дисперсия составляет
4,45
4,34
3,43
4,20
Оценка интенсивности входящего потока для наблюдения в течение времени t над n-канальной системой с очередью длины m, u - число поступивших заявок, принятых на обслуживание, tn+m - общее время полной занятости системы; равна
Плотность распределения непрерывной случайной величины является
знакопеременной
неположительной
ограниченной единицей
неотрицательной
Среднее время ожидания в очереди в одноканальной системе с ограниченной очередью длиной m, интенсивностью потока заявок l, интенсивностью потока обслуживания m, загрузкой системы r и вероятностью p0 - того, что система свободна, r - среднее число заявок в очереди, равно
Свойством марковского случайного процесс является то, что
при известном настоящем его будущее не зависит от прошлого
его конечномерные распределения нормальны
это процесс с дискретным временем
это процесс с независимыми значениями
Соотношение 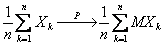 при
при 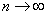 для зависимых случайных величин
для зависимых случайных величин 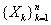
несправедливо
справедливо, если 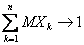
справедливо, если 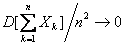
справедливо всегда
Значение функции распределения двумерной случайной величины при равенстве аргументов 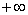 есть
есть
1/2
0
1
Из Минска в Могилев со скоростью 40 км/ч пришла автомашина и сразу же повернула обратно. Скорость ее на обратном пути была на 20 км/ч больше, тогда средняя скорость составила ___ км/ч
48
40
100
60
Ковариационная функция B(t) стационарного случайного процесса как функция аргумента t является
четной
периодической
возрастающей
нечетной
Для невозможного события вероятность равна
0,1
любому числу меньше нуля
0,5
0
В многоканальной системе массового обслуживания n каналов, длина очереди ограничена величиной m; загрузка системы - r; вероятность того, что система свободна, - p0; l и m соответственно интенсивности потока заявок и потока обслуживания. Среднее число заявок в очереди r равно
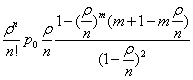
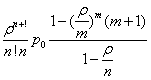
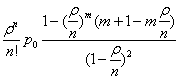
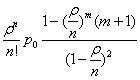
Пусть имеются две независимые выборки, произведенные из генеральных совокупностей с неизвестными теоретическими функциями распределения F1(x) и F2(x). Проверяемая нулевая гипотеза имеет вид Н0: F1(x)=F2(x) против конкурирующей Н1: F1(x)≠F2(x). Будем предполагать, что функции F1(x) и F2(x) непрерывны. Для проверки нулевой гипотезы по критерию Колмогорова-Смирнова используется статистика
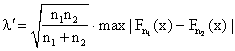 ,где Fn1(x) и Fn2(x) - эмпирические функции распределения, построенные по двум выборкам объемов n1 и n2
,где Fn1(x) и Fn2(x) - эмпирические функции распределения, построенные по двум выборкам объемов n1 и n2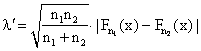 ,где Fn1(x) и Fn2(x) - эмпирические функции распределения, построенные по двум выборкам объемов n1 и n2
,где Fn1(x) и Fn2(x) - эмпирические функции распределения, построенные по двум выборкам объемов n1 и n2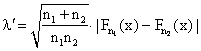 ,где Fn1(x) и Fn2(x) - эмпирические функции распределения, построенные по двум выборкам объемов n1 и n2
,где Fn1(x) и Fn2(x) - эмпирические функции распределения, построенные по двум выборкам объемов n1 и n2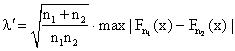 ,где Fn1(x) и Fn2(x) - эмпирические функции распределения, построенные по двум выборкам объемов n1 и n2
,где Fn1(x) и Fn2(x) - эмпирические функции распределения, построенные по двум выборкам объемов n1 и n2Пусть 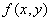 - плотность вероятностей случайного вектора
- плотность вероятностей случайного вектора 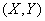 ,
, 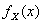 и
и 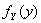 - плотности вероятностей координат этого вектора, причем
- плотности вероятностей координат этого вектора, причем 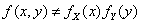 , тогда случайные величины
, тогда случайные величины 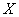 и
и 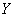
независимы
зависимы
линейно зависимы
коррелированы
Безразмерная характеристика, выражающая тесноту связи между признаками в числовой форме, называется
коэффициентом корреляции
отношением их эмпирических дисперсий
ковариацией
коэффициентом детерминации
Из 11 спортсменов физкультурной группы 6 перворазрядников. Вероятность того, что среди 2 случайно выбранных спортсменов окажется два перворазрядника, равна
0,11